Файл: Практикум 6 (тема Умозаключение) Задание 1 Приведите два примера правильных простых категорических силлогизмов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практикум 6 (тема «Умозаключение»)
Задание 1 Приведите два примера правильных простых категорических силлогизмов.
Ответ: Он состоит из трех категорических суждений, два из которых являются посылками, а третье-заключением.
Задание 2 Приведите два примера неправильных простых категорических силлогизмов. Покажите их неправильность с помощью кругов Эйлера.
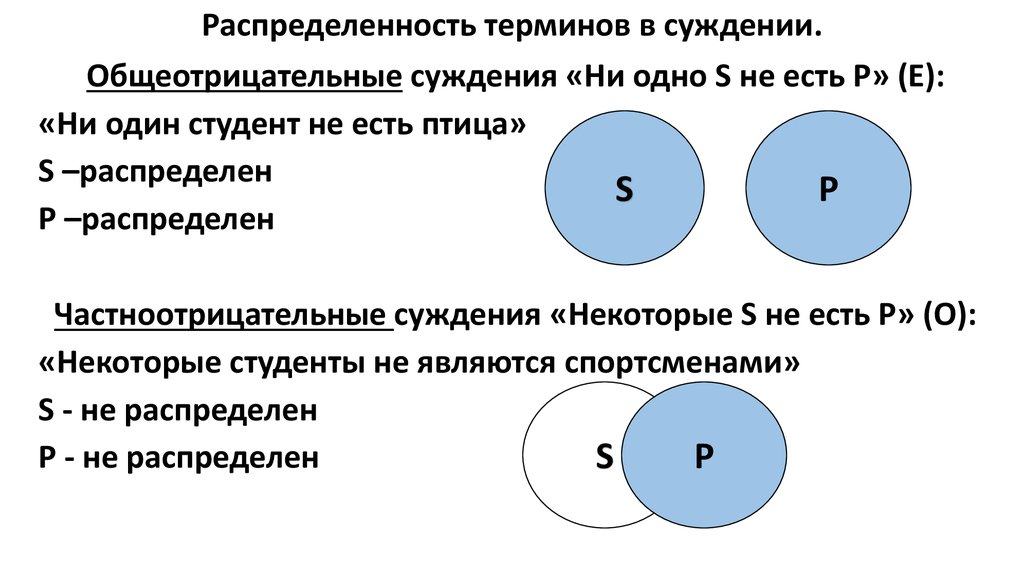
Задание 3 Приведите по одному примеру следующих способов рассуждения: а) modus ponens; б) modus tollens; в) modus ponendo tollens; г) modus tollendo ponens.
Ответ: А) Modus ponens это верное заключение, состоящее в переходе от истинности посылки к истинности ее необходимого следствия. Modus ponens принимает форму: если р, то q однако р, следовательно, q. Пример Modus ponens: Если Сократ человек, то он смертен; однако Сократ человек, следовательно, Сократ смертен.
Б) Modus tollens это верное заключение, приводящее к выводу о ложности посылки исходя из ложности по меньшей мере одного из ее следствий и принимающее форму: если р, то q; однако не q, следовательно, не р. Пример Modus tollens: Eсли Сократ бог, то он бессмертен; однако Сократ не бессмертен, следовательно, он не бог.
В) Modus ponendo tollens. В этом силлогизме в меньшей посылке утверждается один из членов деления большей посылки, или одна альтернатива; в заключение же вследствие этого все остальные члены отрицаются.
Его форма:
A есть или B, или C, или D, или E.
A есть B.
Следовательно, A не есть ни C, ни D, ни E.
Пример:
Треугольники бывают или остроугольные, или тупоугольные, или прямоугольные. Данный треугольник есть остроугольный.
Следовательно, он не есть ни прямоугольный, ни тупоугольный.
Для правильности этого вида умозаключения необходима правильность большей посылки, т.е. необходимо, чтобы члены деления были перечислены сполна и чтобы они исключали друг друга.
Г) Modus tollendo ponens. В этой форме, в противоположность предыдущей, в меньшей посылке отрицаются все члены деления, за исключением одного, который и утверждается в заключении.
Его схема:
A есть или B или C, или D.
A не есть ни B, ни C.
Следовательно, A есть D.
Пример:
Треугольники бывают или остроугольные, – или тупоугольные, или прямоугольные.
Данный треугольник не есть ни остроугольный, ни тупоугольный. Следовательно, он – прямоугольный.
Этот вид разделительных умозаключений употребляется в геометрии под именем непрямого доказательства. Например:
Известная сумма должна быть или больше, или меньше, или равна тому-то.
Но она ни больше, ни меньше.
Следовательно, она равна.
Условие правильности разделительного силлогизма, как это легко видеть, сводится к правильности разделительных суждений, входящих в качестве посылки в состав разделительного силлогизма.