Файл: Степенной ряд в общем виде записывается следующим образом a.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 22
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задание 2
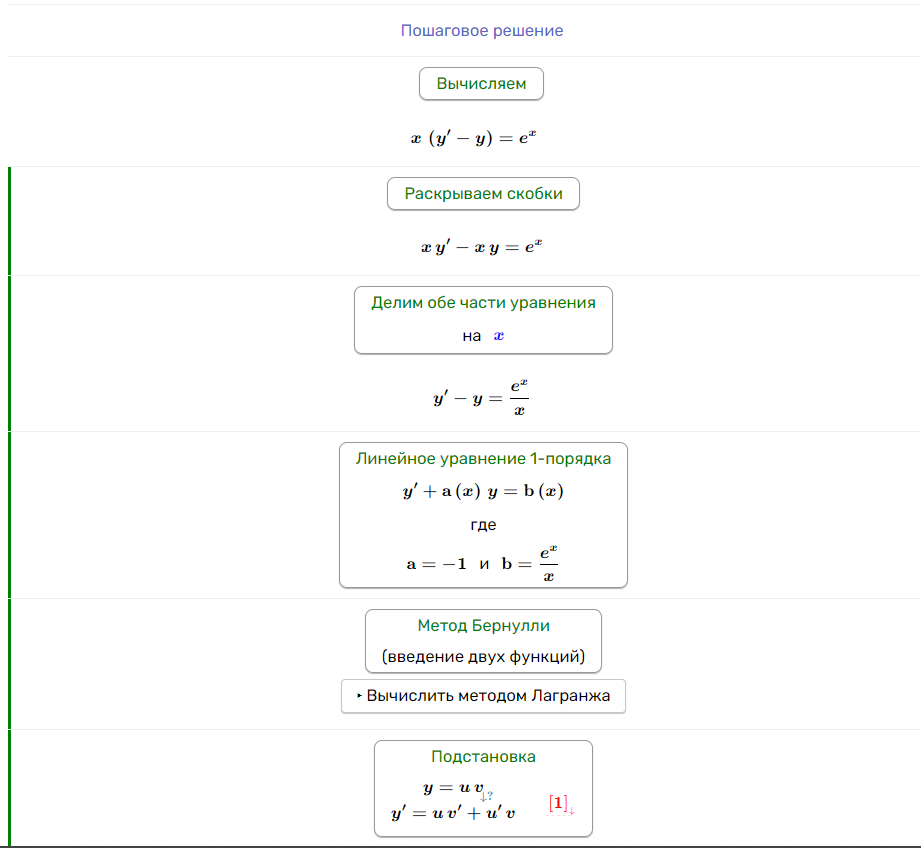
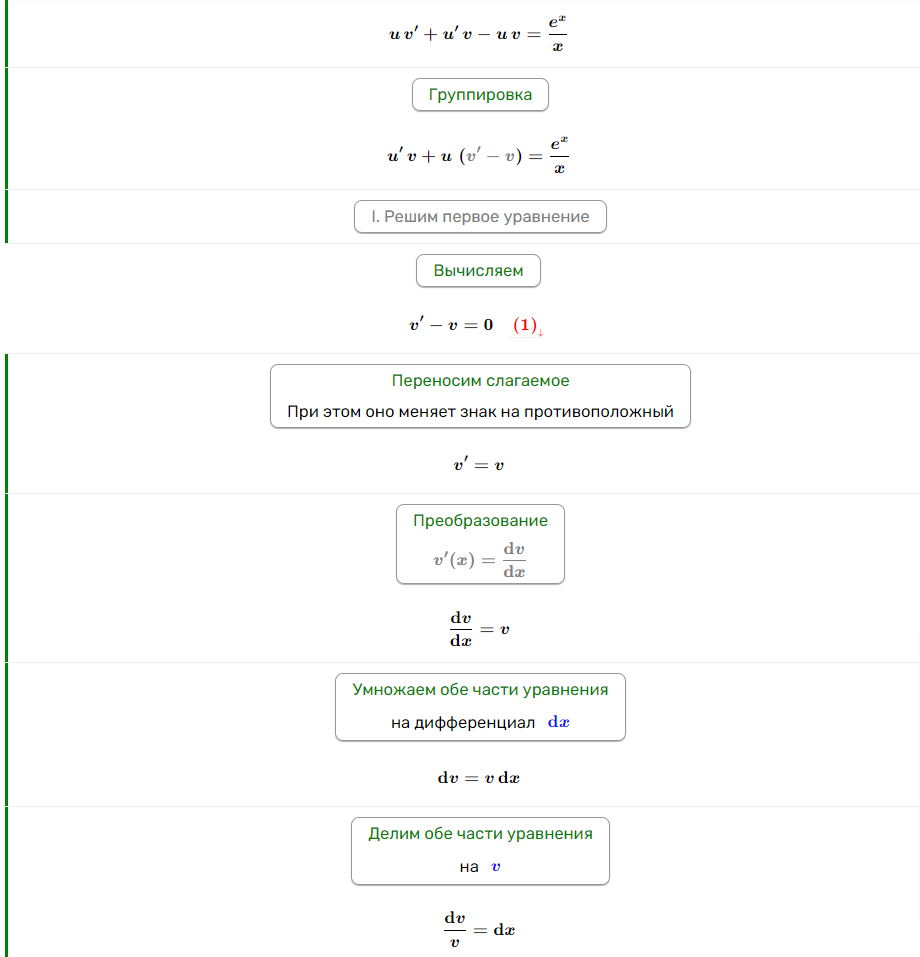

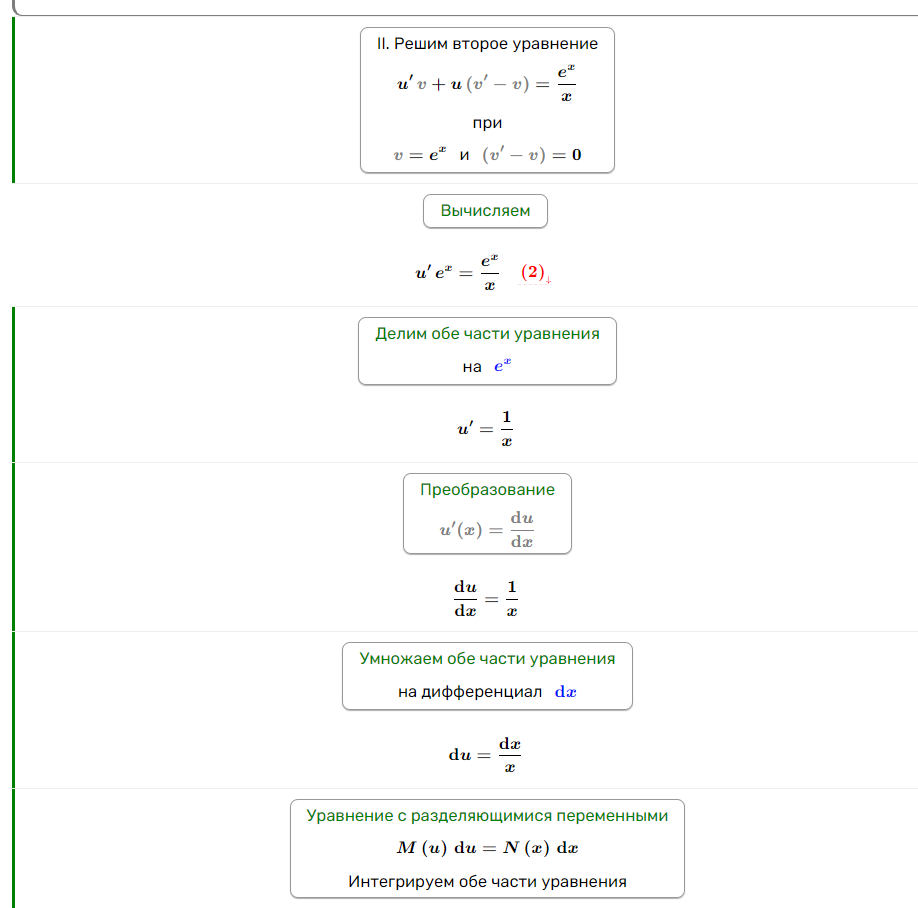
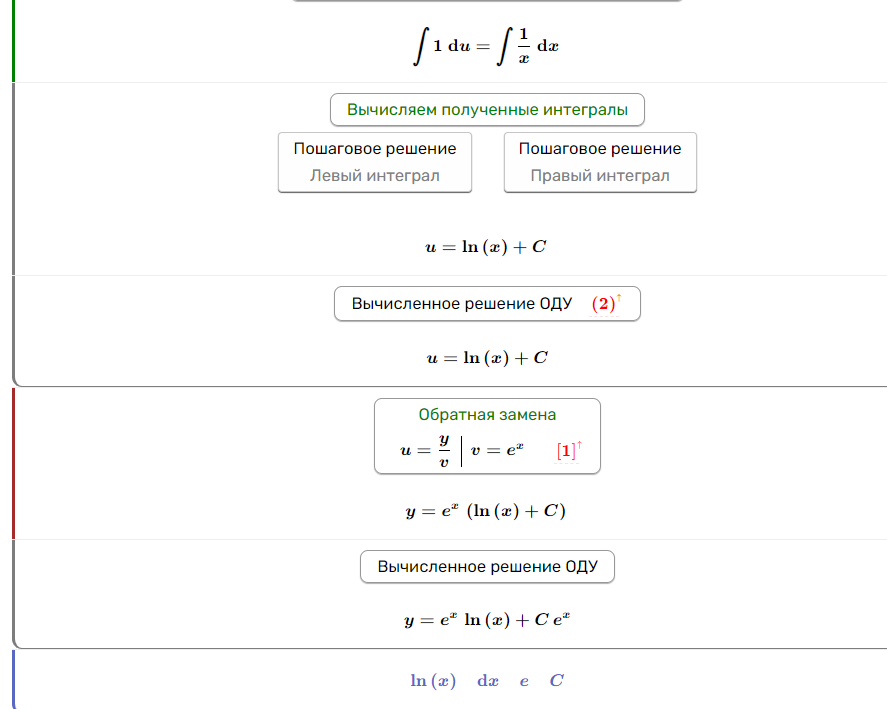
Задание 3
Степенной ряд в общем виде записывается следующим образом: ∑anxn
где an - формула числовых коэффициентов. Для данного ряда:
an=
Областью сходимости степенного ряда является интервал (-R;R), где:
R - радиус сходимости. Вычислим его:
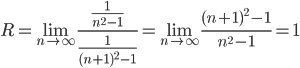
x1 = -5 - 1 = -6
x2 = -5 + 1 = -4
Итак, ряд является сходящимся (абсолютно) при всех x, принадлежащих интервалу (-6;-4)
Теперь проверим сходимость ряда на концах этого интервала.
Пусть x=-6
Получаем ряд:
Исследуем сходимость ряда при помощи признаков сходимости.
Рассмотрим первые три члена ряда:
-∞
,
Это числовой знакопеременный ряд, исследуем его по признаку Лейбница.
а) По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
∞
>
б) По второму признаку Лейбница предел ряда должен стремится к 0.
Второе условие Лейбница выполняется.
Таким образом, рассматриваемый ряд сходится.
Чтобы говорить об абсолютной или условной сходимости, необходимо исследовать ряд по одному из признаков сходимости рядов.
Используем предельный признак сравнения. Сравним исследуемый ряд с рядом:
Этот ряд будет сходиться (α=2 > 1).
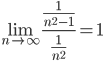
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится.
Следовательно, ряд сходится абсолютно.
Ряд сходится, значит, x=-6 - точка сходимости.
При x=-4 получаем ряд:
Исследуем его сходимость при помощи признаков сходимости.
Используем предельный признак сравнения. Сравним исследуемый ряд с рядом:
Этот ряд будет сходиться (α=2 > 1).
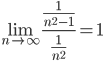
Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится.
Следовательно, ряд:
Значит, x = -4 - точка сходимости.
Таким образом, данный степенной ряд является сходящимся при:
x∈ [-6;-4]
Задание 4
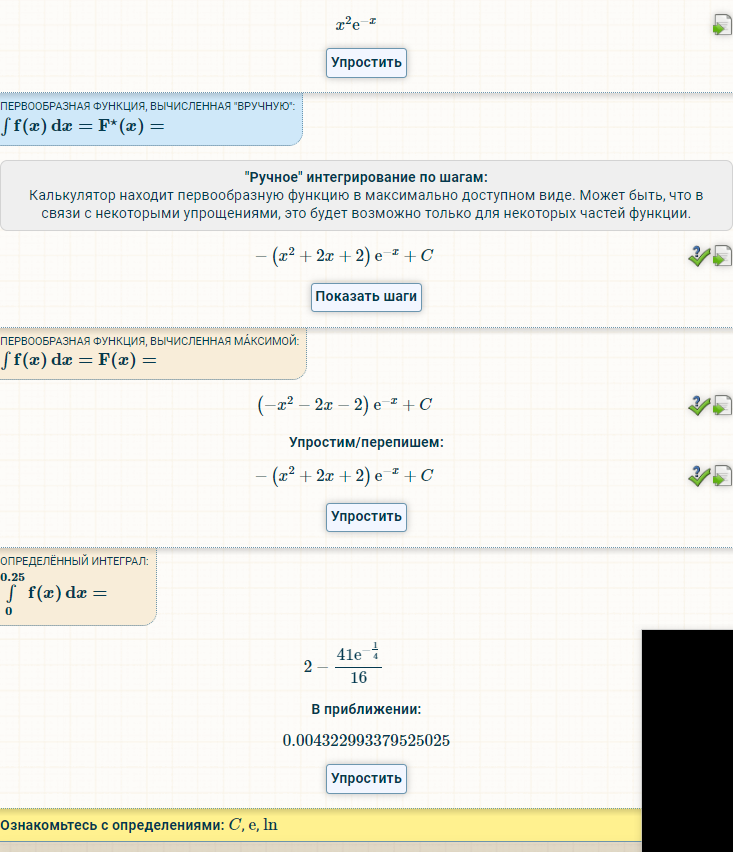
5 хз
Задание 6
ln(-5·i)
Представим в показательной форме:
t=eln(i·(-5))=-5·i
z=-5·i
Представим
как:
z=(-5)·i
Для упрощения вычислений найдем все характеристики для
z=i
, а модуль числа умножим на -5
1. Находим тригонометрическую форму комплексного числа.
Действительная часть числа x.
x=Re(z)=0
Мнимая часть числа y.
y=Im(z)=1
Модуль комплексного числа |z|.
С учетом -5 получаем:
|z|=-5·1=-5
Поскольку x = 0, y > 0, то arg(z) находим как:
arg(z)
=
φ
=
Таким образом, тригонометрическая форма комплексного числа:
2. Находим показательную форму комплексного числа.
z
=
|z|·ei·φ
=
Обратно логарифмируем:
z
=
ln(t)
=
Ответ:
Тут все остальные задания по дискретке
https://topuch.com/kontrolenaya-rabota-po-discipline-diskretnaya-matematika-vipol/index.html