ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 10
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1.
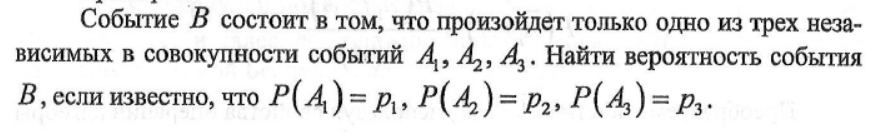
Решение
Задача 2.
Из урны, содержащей 1 белый, 2 красных и 3 черных шаров случайным образом вынимают 3 шара. Найти вероятности следующих событий:
-
шары одного цвета; -
два шара одного цвета, третий другого; -
все шары разных цветов.
Решение
Всего 1+2+3=6 шаров.
Количество способов выбора 3х шаров из 6:
.-
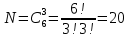Найдем вероятность того, что все шары одного цвета. Мы можем вытащить только 3 черных шара (так как белых и красных у нас меньше 3)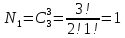
способами.
Тогда по классическому определению вероятности
-
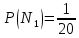
Найдем вероятность то, что вытащили два шара одного цвета и 1 другого. Возможные варианты: ккб, ккч, ччб, ччк.
Два красных и один белый можно выбрать
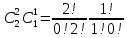=1 способом.Аналогично для случаев 2 красных+1 черный, 2 черных+1 белый, 2 черных+1 красный.
Тогда по теореме сложения (наши события несовместны) и умножения (события независимы) вероятность
-
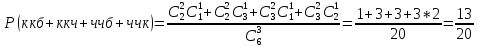
Найдем вероятность, что все три шара разных цветов
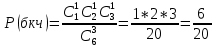
Стоит отметить, что перечисленные варианты представляют полную группу событий (то есть других комбинаций быть не может). Поэтому сумма всех трех вероятностей должна быть равна 1. Проверим это:
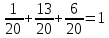
Задача 3.
Найти вероятность того
, что при 10 бросках монеты орёл выпадет 3 раза.
Решение.
Сначала немного порассуждаем: всего проводится 10 повторных независимых испытаний. Сколькими способами можно выбрать 3 испытания, в которых выпадет орёл?
способами!Используем формулу Бернулли:
, в данном случае:
– всего испытаний;
– количество испытаний, в которых должен появиться орёл;
– вероятность появления орла в каждом испытании;
– вероятность появления решки в каждом испытании.Таким образом:
– вероятность того, что при 10 бросках монеты орёл выпадет ровно 3 раза.Задача 4.
Монета подбрасывается 400 раз. Найти вероятность того, что орёл выпадет ровно 200 раз.
Решение.
Найдём вероятность того, что в серии из 400 бросков орёл выпадет ровно
раз. Ввиду большого количества испытаний используем локальную теорему Лапласа: 
, где 
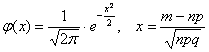.На первом шаге вычислим требуемое значение аргумента:
Существует таблица значений функции
, которая есть практически в любой книге по теории вероятностей.
На заключительном этапе применим формулу
:
– вероятность того, что при 400 бросках монеты орёл выпадет ровно 200 раз.Задача 5.
Вероятность поражения стрелком мишени равна 0,7. Найти вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Решение.
В данной задаче речь идёт о повторных независимых испытаниях, причём их количество достаточно велико. По условию требуется найти вероятность того, что мишень будет поражена не менее 65, но и не более 80 раз, а значит, нужно использовать интегральную теорему Лапласа:
, где 
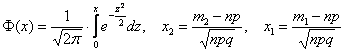
Для удобства перепишем исходные данные в столбик:
– всего выстрелов;
– минимальное число попаданий;
– максимальное число попаданий;
– вероятность попадания в мишень при каждом выстреле;
– вероятность промаха при каждом выстреле.
.Вычислим значения аргументов:
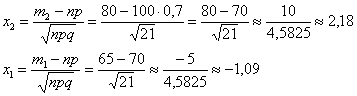
Значения функции
найдём по соответствующей таблице:
– вероятность того, что при 100 выстрелах мишень будет поражена от 65 до 80 раз.
Обязательно пользуемся нечётностью функции! На всякий случай распишу подробно:
