Добавлен: 25.10.2023
Просмотров: 69
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МЕЛИТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
Агротехнологический факультет
Кафедра «Гражданская безопасность»
Реферат
На тему: Метод Монжа
Выполнил: 11-ГБ,
Проверил: Пыхтеева И.В.
Журба В.Н.
Мелитополь - 2023
Метод Монжа.
Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, т. е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем простых приемов определить размеры отрезков линий и фигур. Постепенно накопившиеся отдельные правила и приемы построений таких изображений были приведены в систему и развиты в труде французского ученого Монжа, изданном в 1799 г. под названием «Geometrie descriptive».
Гаспар Монж (1746 – 1818) вошел в историю как крупный французский геометр конца XVIII и начала XIX вв., инженер, общественный и государственный деятель в период революции 1789–1794 гг. и правления Наполеона I, один из основателей знаменитой Политехнической школы в Париже, участник работы по введению метрической системы мер и весов. Будучи одним из министров в революционном правительстве Франции, Монж много сделал для ее защиты от иностранной интервенции и для победы революционных войск. Монж не сразу получил возможность опубликовать свой труд с изложением разработанного им метода. Учитывая большое практическое значение этого метода для выполнения чертежей объектов военного значения и не желая, чтобы метод Монжа стал известен вне границ Франции, ее правительство запретило печатание книги. Лишь в конце XVIII столетия это запрещение было снято. После реставрации Бурбонов Гаспар Монж подвергся гонению, вынужден был скрываться и кончил свою жизнь в нищете.
Изложенный Монжем метод – метод параллельного проецирования (причем берутся прямоугольные проекции на две взаимно перпендикулярные плоскости проекций) – обеспечивая выразительность, точность и удобоизмеримость изображений предметов на плоскости, был и остается основным методом составления технических чертежей.
Слово прямоугольный часто заменяют словом ортогональный, образованным из слов древнегреческого языка, обозначающих «прямой» и «угол». В дальнейшем изложении термин ортогональные проекции будет применяться для обозначения системы прямоугольных проекций на взаимно перпендикулярных плоскостях.
1.5. Проецирование на две взаимно перпендикулярные плоскости проекций
Обратимость чертежа может быть обеспечена проецированием на две непараллельные плоскости проекций.
Для удобства проецирования в качестве двух плоскостей проекций выбирают две взаимно перпендикулярные плоскости (рис.1.8). Одну из них принято располагать горизонтально – ее называют горизонтальной плоскостью проекций, другую – вертикально. Вертикальную плоскость называют фронтальной плоскостью проекций. Эти плоскости проекций пересекаются по линии, называемой осью проекций.
Ось проекций разделяет каждую из плоскостей проекций на две полуплоскости.
Обозначим плоскости проекций буквами: V – фронтальную, H – горизонтальную, ось проекций – буквой x или в виде дроби V/H.Плоскости V и H образуют систему V, H.(Наряду с указанными обозначениями плоскостей проекций в литературе применяют и другие обозначения, например буквой π с индексами.)
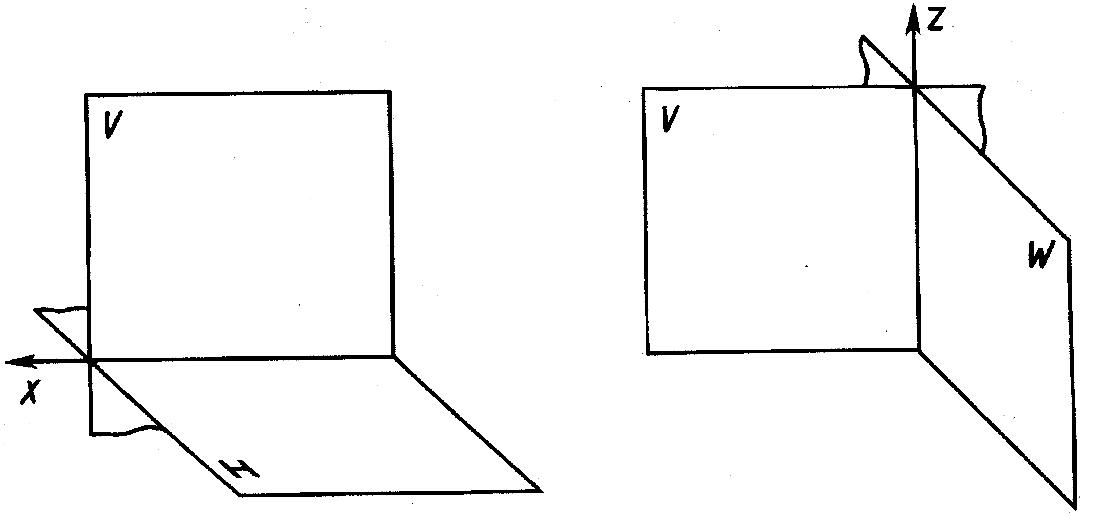
Рис.1.8 Рис.1.9
Плоскости проекций, пересекаясь, образуют четыре двугранных угла, из которых приведенный на рисунке 1.8 (с обозначениями граней V, H) считают первым.
В промышленности чертежи многих деталей выполняют также в системе двух взаимно перпендикулярных плоскостей, пересекающихся по вертикальной оси проекций z (рис.1.9). При этом фронтальной плоскостью проекций оставляют также плоскость V, а перпендикулярную к ней и обозначаемую W называют профильной плоскостью проекций.
В системе двух взаимно перпендикулярных плоскостей проекций горизонтальной проекцией точки называют прямоугольную проекцию точки на горизонтальной плоскости проекций
;
фронтальной проекцией точки называют прямоугольную проекцию точки на фронтальной плоскости проекций.
Наглядное изображение построения проекций произвольной точки А в системе V, H показано на рисунке 1.10. Горизонтальную проекцию, обозначенную а, находят как пересечение перпендикуляра, проведенного из точки А к плоскости H, с этой плоскостью. Фронтальную проекцию, обозначенную a', находят как пересечение перпендикуляра, проведенного из точки А к плоскости V, с этой плоскостью.
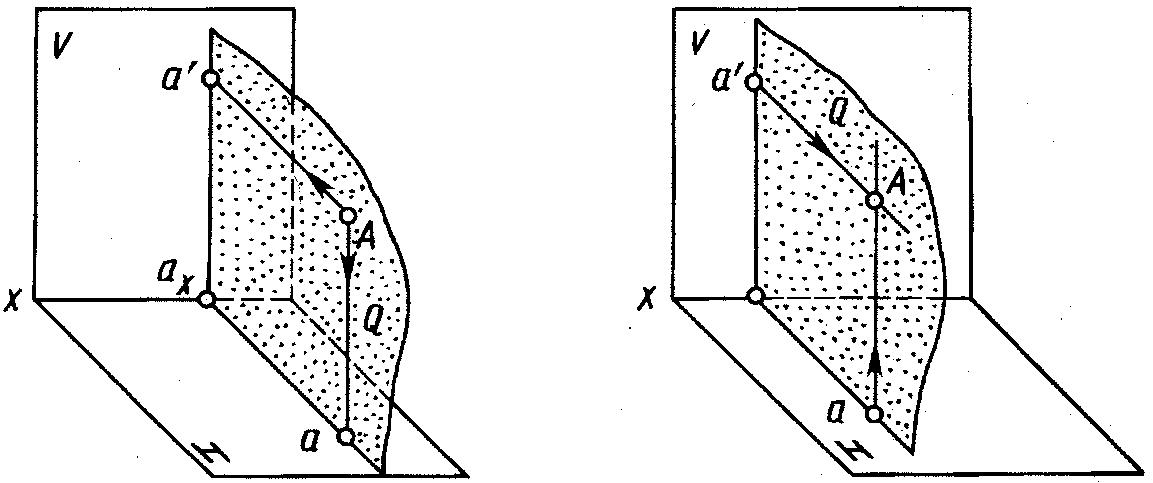
Рис. 1.10 Рис. 1.11
Проецирующие прямые Aa' и Aa, перпендикулярные к плоскостям H и V, принадлежат плоскости Q.Она перпендикулярна плоскостям проекций и пересекает ось проекций в точке ах.Три взаимно перпендикулярные плоскости Q, V и H пересекаются по взаимно перпендикулярным прямым, т. е. прямые а'ах, аах иось x взаимно перпендикулярны.
Построение некоторой точки А в пространстве по двум заданным ее проекциям – фронтальной а' и горизонтальной а – показано на рисунке 1.11. Точку А находят на пересечении перпендикуляров, проведенных из проекции а' к плоскости V и из проекции а к плоскости H. Проведенные перпендикуляры принадлежат одной плоскости Q, перпендикулярной к плоскостям V и H, и пересекаются в единственной искомой точке А пространства.
Таким образом, две прямоугольные проекции точки вполне определяют ее положение в пространстве относительно данной системы взаимно перпендикулярных плоскостей проекций.
В дальнейшем прямоугольные проекции точки в системе взаимно перпендикулярных плоскостей проекций будем называть ортогональными проекциями точки.
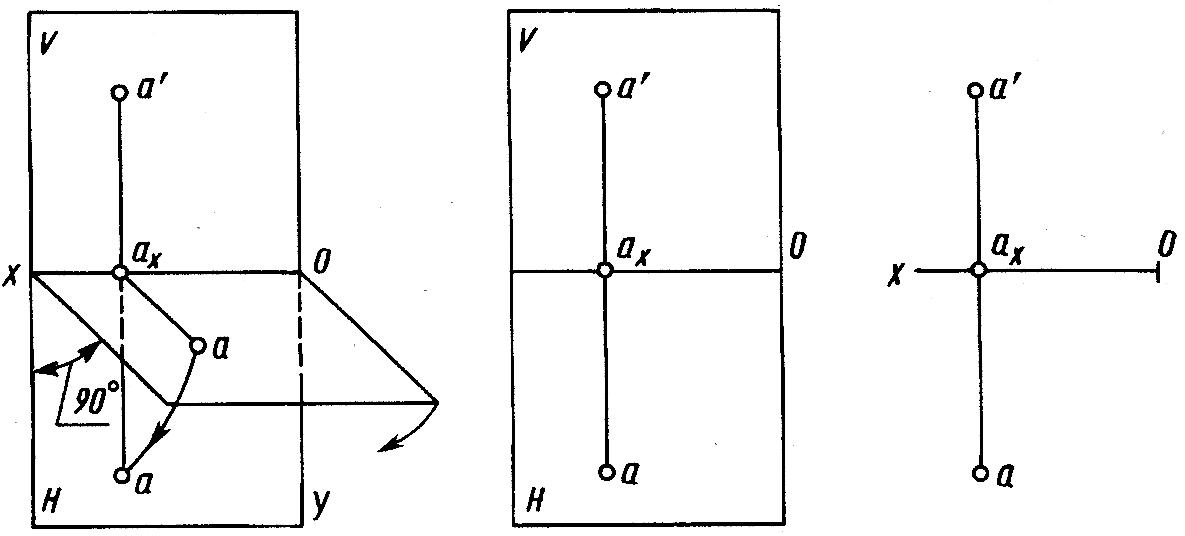
Рис. 1.12 Рис. 1.13 Рис. 1.14
Рассмотренное наглядное изображение точки в системе V, H неудобно ввиду своей сложности для целей черчения. Преобразуем его так, чтобы горизонтальная плоскость проекций совпадала с фронтальной плоскостью проекций, образуя одну плоскость чертежа. Это преобразование осуществляют (рис.1.12) путем поворота вокруг оси
x плоскости H на угол 90° вниз. При этом отрезки ах а' и ах а образуют один отрезок a'a, перпендикулярный оси проекции, называемый линией связи.В результате указанного совмещения плоскостей V и H получается чертеж – рисунок 1.13, известный под названием эпюр (от французского epure – чертеж, проект) или эпюр Монжа. Этот чертеж в системе V, H (или в системе двух прямоугольных проекций) называют двухкартинным чертежом Монжа. Без обозначения плоскостей V и H этот чертеж приведен на рисунке 1.14.