Файл: 2. Решение каждой части в программе реализовать в виде процедуры.docx

Скачать файл (0,51Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 20

Скачиваний: 3

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Уфимский государственный нефтяной технический университет»

Кафедра вычислительной техники и инженерной кибернетики

ОТЧЁТ

по лабораторной работе №5

“Обработка двумерных массивов данных”

Вариант № 41

Выполнил: ст. гр. Б___-21-0_ А.Р Асадуллина
Проверил:

Ассистент кафедры ВТИК З.Р.Хасанова

Уфа 2022

Постановка задачи

Разработать программу получения и обработки двумерного массива, состоящую из 5 частей.

_Часть1.Создание двумерного массива с помощью формулы

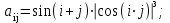
Часть 2 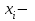скалярное произведение побочной диагонали на i-й столбец;

Часть 3.

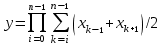
Часть 4.построить матрицу, обратную к транспонированной исходной матрице;

Часть 5.умножить обратную матрицу на вектор х
Обязательные требования к программе.
1. Программу разработать для решения задачи в общем виде, для произвольных значений исходных данных: количества элементов n (2<=n<=100).

2. Решение каждой части в программе реализовать в виде процедуры.

Анализ задачи.

Исходными данными являются значения количества элементов в массиве n

Порядок решения задачи: сначала нужно получить двумерный маcсив (часть 1), затем можно вычислить x_i(часть 2) затемвычислитьзначение y (часть 3)(часть 4) в конце мы должны.построить матрицу, обратную к транспонированной исходной матрице;

. (часть 5)

Часть 1.

Возьмем любые исходные данные, например n=2, Теперь мы можем создать двумерный массив с помощью формулы:

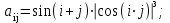
Вычислив каждый элемент матрицы по данной формуле, получим:

0.143 0.010

0.010 -0.211

Часть 2.

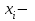скалярное произведение побочной диагонали на i-й столбец;
Элементы побочной диагонали

0,010 0,010

Например i=1

0,143

0,010

_{=0,010*0,143, 0,010*0,010}

х i=0,00143 ,0,0001
Часть 3.

Значение yвычисляется по sum:=sum+(x[k-1]+x[k+1])/2; y:=y*sum;

Значение y равно: 0.0028727

Часть 4. Чтобы построить транспонированную матрицу надо

t:=a[i,j];

a[i,j]:=a[j,i]

t:=a[j,i];

В итоге получится:

0,143 0,010

0,010 -0,211

Чтобы построить обратную матрицу надо единицу разделить на соответствующий элемент .

r[i,j]:= b[i,j];

b[i,j] := 1/r[i,j];

r[i,j]:= b[i,j];
Часть 5.

Матрица А:

0.143 0.010 -0.734 -0.268

0.010 -0.211 -0.849 -0.001

-0.734 -0.849 -0.211 0.395

-0.268 -0.001 0.395 0.869

Сформируем вектор Х по формуле :

0.072 0.001 -0.335 -0.233

Найдем обратную матрицу транспонированной исходной матрицы:

6.972 98.327 -1.362 -3.734

98.327 -4.731 -1.178 -1161.877

-1.362 -1.178 -4.732 2.533

-3.734 -1161.877 2.533 1.151

И умножим обратную матрицу на вектор Х:

-0.019 0.000 -0.132 -0.202

Алгоритм решения задачи

При разработке алгоритме будем использовать метод декомпозиции: решение задачи сначала опишемв виде основного алгоритма, использующего вспомогательные алгоритмы решения задач частей задания. Затем опишем вспомогательные алгоритмы – модули решения задач каждой части. При разработке и описании алгоритмов используются элементарные структуры алгоритмов, составляющие основу структурного программирования.

Основной алгоритм.

При разработке основного алгоритма нужно учесть обязательные требования, сформулированные в постановке задачи и рекомендации по разработке сложных программ:

Необходимозадачу решать в общем виде, для любых допустимых значений исходных данных.
Модули должны быть относительно независимы: обязательно иметь имя, свои входные, выходные и промежуточные данные, не использовать глобальные переменные, ввод и вывод данных в модуле может быть только в случае необходимости.
Действия алгоритма поясняются на естественном языке, в обозначениях постановки задачи, не используются конструкции языка программирования