Добавлен: 25.10.2023
Просмотров: 21
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Бланк выполнения задания 1
Задача 1.
Задание:
Частица движется равноускоренно в координатной плоскости XY с начальной скоростью
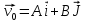и ускорением 
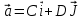. Найти модули векторов скорости 
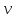, тангенциального 
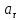и нормального 
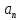ускорений, а также радиус кривизны траектории R в момент времени t.Вводные данные:
| Вариант | A, м/с | B, м/с | C, м/с2 | D, м/с2 | t, с |
| 1 | 5 | 2 | 5 | 3 | 1 |
Решение:
Координаты вектора начальной скорости
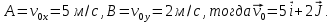
Координаты вектора ускорения
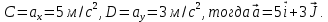
Уравнения траектории частиц
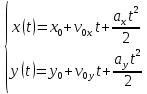
За начало координат примем точку начала движения. Тогда после подстановки координат начальной скорости и ускорения получаем
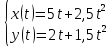
Скорость частицы в момент времени t
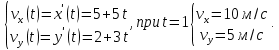
Тогда модуль вектора скорости
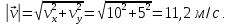
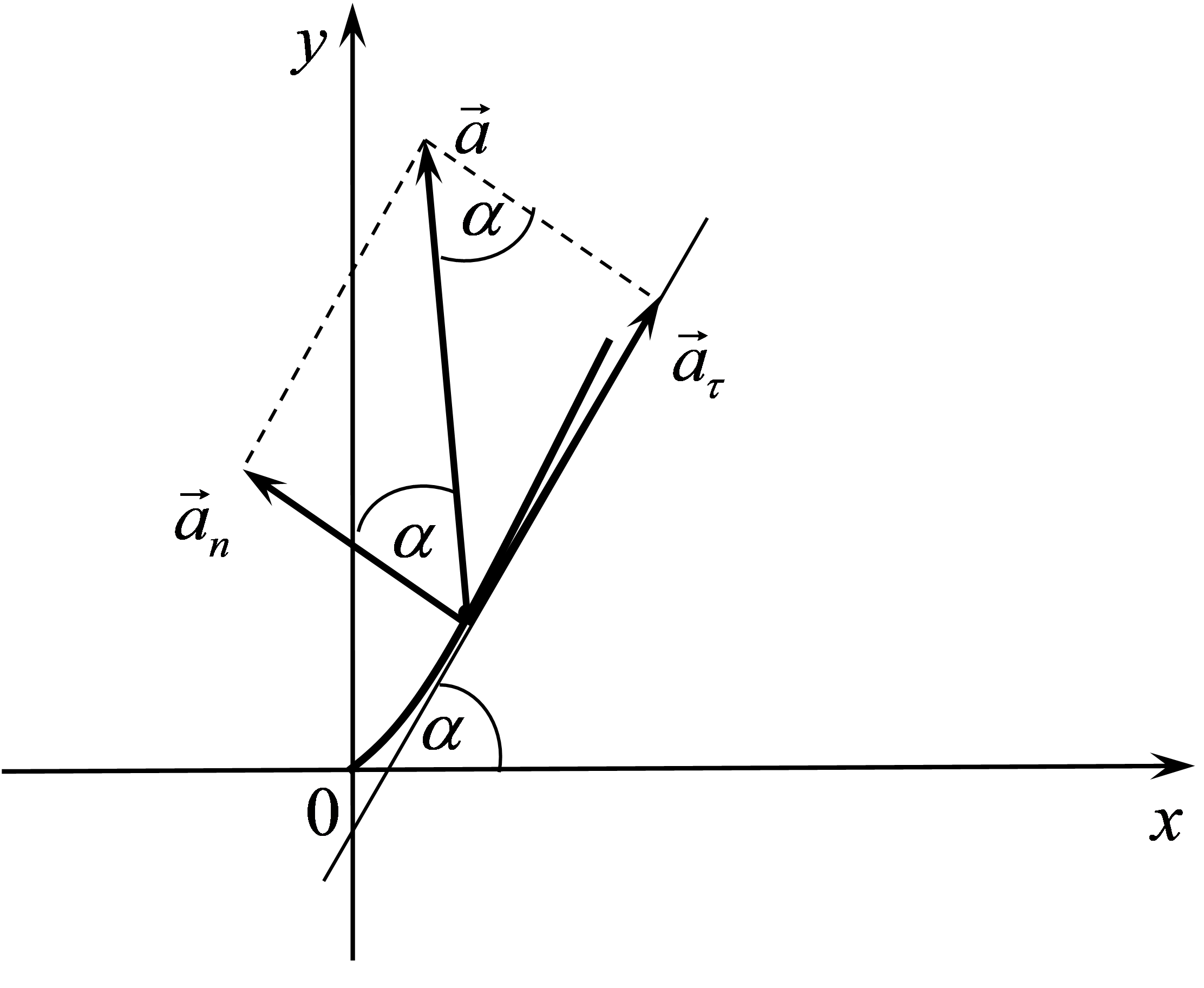
Рис. 1. График траектории частицы.
Полное ускрение
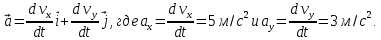
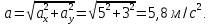
Тангенс угла, который образует касательная к траетории в момент времени
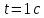
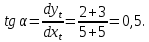
Тогда
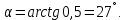
Следовательно
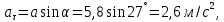
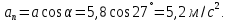
Формула нормального ускорения
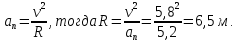
Ответ:
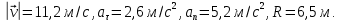
Задача 2.
Задание:
На однородный цилиндрический блок массой m2 и радиусом R намотана невесомая нить, к свободному концу которой прикреплен груз массой m1. К блоку крестообразно прикреплены четыре одинаковых невесомых стержня, на которых закреплены одинаковые грузы массой m3 на расстоянии x от оси вращения. Грузы m3 можно считать материальными точками. Трением в блоке можно пренебречь. Найти зависимость ускорения a груза m1 от расстояния x . Построить график этой зависимости в интервале изменения x от R до 3R . Ускорение свободного падения g = 9.81 м/с2.
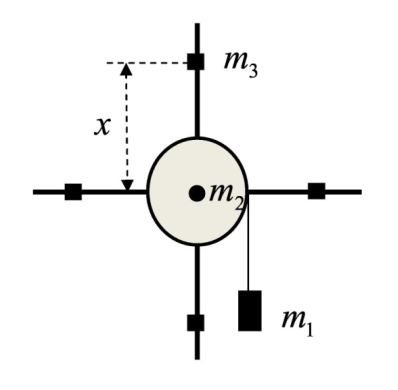
Рис. 2. Расчетная система.
Вводные данные:
| Вариант | m1, кг | m2, кг | m3, кг | R, м |
| 1 | 3 | 2 | 1 | 0,2 |
Решение:
По закону сохранения энергии потенциальная энергия груза m1 преобразуется в поступательную кинетическую энергию груза m1 и вращательную кинетическую энергию блока m2 и грузов m3
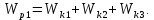
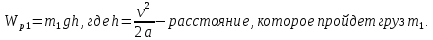
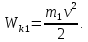
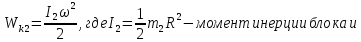
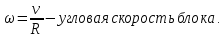
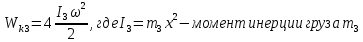
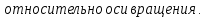
Тогда
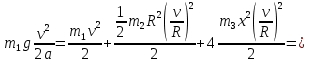
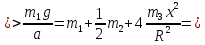
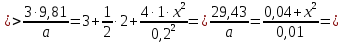
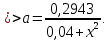
Построим график зависимости
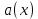для 
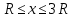
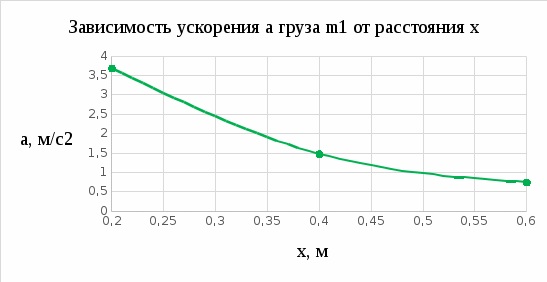
Ответ:
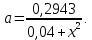
Задача 3.
Задание:
Шар массой
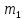, летящий со скоростью 
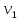, сталкивается с неподвижным шаром массой 
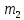. После удара шары разлетаются под углом 
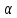друг к другу. Удар абсолютно упругий, столкновение происходит в горизонтальной плоскости. Найти скорости шаров 
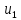и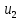 
после удара.Вводные данные:
| Вариант | m1, г | m2, г | v1, м/с |  |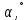
| 1 | 100 | 150 | 10 | 120 |
Решение:
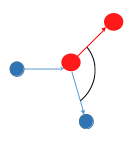
Рис. 3. Упругое соударение шаров.
По закону сохранения кинетической энергии
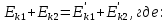
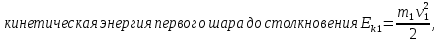
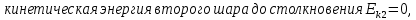
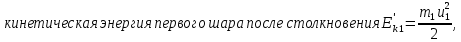
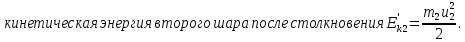
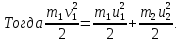
По закону сохранения импульса
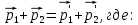
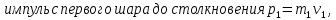
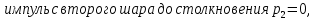
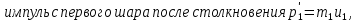
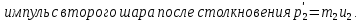
Тогда результирующий вектор импульса после столкновения шаров по теореме косинусов
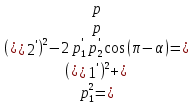
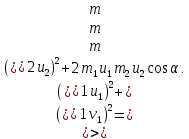
Решим полученную систему уравнений
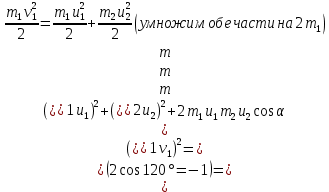
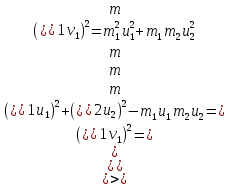
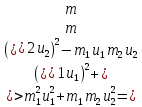
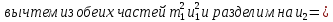
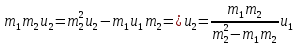
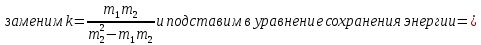
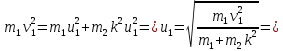
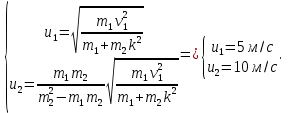
Ответ:
