Файл: Решение. Уравнение не содержит явно переменную, поэтому применим замену.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 25.10.2023

Просмотров: 52

Скачиваний: 2

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Автономная некоммерческая организация высшего образования

«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра общегуманитарных наук и массовых коммуникаций
Форма обучения: очно-заочная
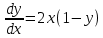
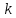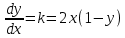
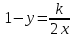
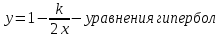
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕМатематикаГруппа 22М516вСтудентЕ.А. СазоновМОСКВА 20231. Методом изоклин построить интегральные кривые уравнения: Решение.Построим поле направлений для данного дифференциального уравнения. Изоклины, соответствующие направлениям поля с угловым коэффициентом равным , естьилиПостроим изоклины для 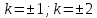и прямую 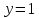при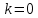 . 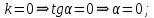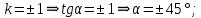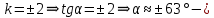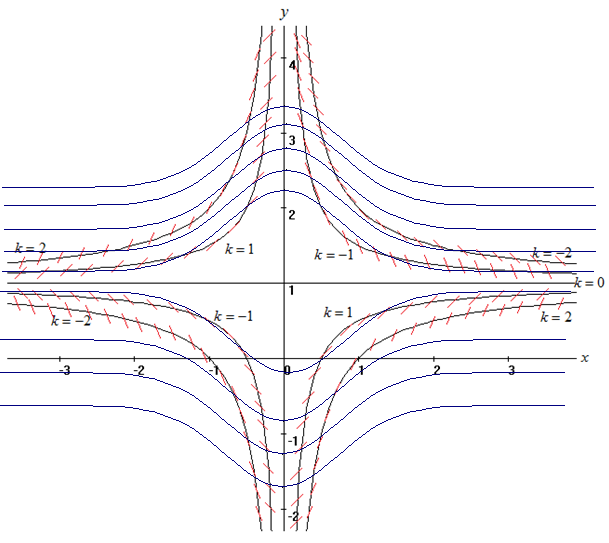Засечками отметим отрезки с соответствующими угловыми коэффициентами углы, которые образуют отрезки с положительным направлением оси абсцисс.Построим несколько интегральных линий, которые будут пересекать изоклины под углом, заданным полем направления.2. Решить уравнение, допускающее понижения порядка:

.

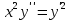
Решение.

Уравнение не содержит явно переменную 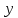, поэтому применим замену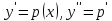



тогда получим:



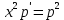
Разделяем переменные:





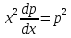
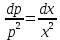
Интегрируем обе части полученного уравнения:





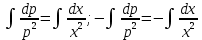
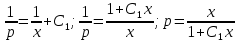
Возвращаемся к замене:



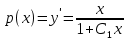
Разделяем переменные:





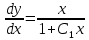
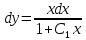
Интегрируем обе части полученного уравнения:







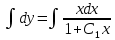
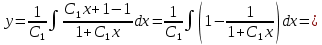
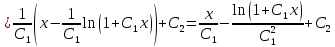
Ответ:



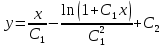
3. Решить систему уравнений:



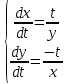
Решение.

По формуле производной параметрической функции:





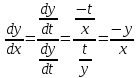
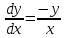
Разделяя переменные и интегрируя, получим:







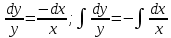
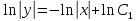
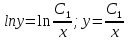
Подставляем полученное значение 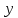в первое уравнение системы: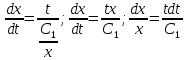







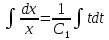
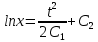
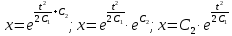
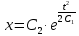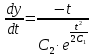
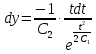
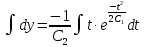
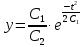
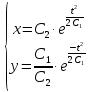
Подставляем значение во второе уравнение системы:Ответ: 4. Вероятность появления события в каждом испытании равна 0,7. 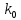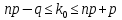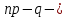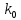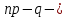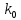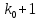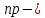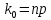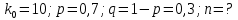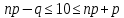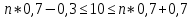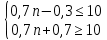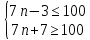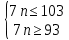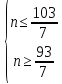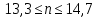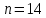Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10?Решение.Наивероятнейшее число определяют из двойного неравенства:причем:а) если число дробное, то существует одно наивероятнейшее число ;б) если число целое, то существует два наивероятнейших числа, а именно и ;в) если целое число, то наивероятнейшее число .По условию:Ответ: 14.

Смотрите также файлы