Файл: Отчет по лабораторной работе 1 По дисциплине Процессы и аппараты химической технологии.docx
Добавлен: 25.10.2023
Просмотров: 12
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»
Комплексная учебная лаборатория факультета переработки минерального сырья ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1
По дисциплине Процессы и аппараты химической технологии
(наименование учебной дисциплины согласно учебному плану)
Тема работы: Изучениережимовтеченияжидкости
| Выполнил: студент гр. ТХ-21-2 | | СмяткинаА.Д. |
| (шифр группы) Оценка: | (подпись) | (Ф.И.О.) |
| Дата: | | |
| Проверил | | |
| руководитель работы: доцент | | ЗыряноваО.В. |
| (должность) | (подпись) | (Ф.И.О.) |
Санкт-Петербург 2023
Цель работы: изучить режимы течения жидкости и определить от чего они зависят.
Краткие теоретические сведения
Идеальнаямодельжидкости— модель жидкости, в которой взаимное перемещение частиц с неизменной скоростью
не встречает сопротивления и не требует затрат энергии.
Модельслоистогодвижения— модель жидкости, в которой частицы, обладающие разными скоростями, движутся равномерно и прямолинейно в разных прилегающих друг к другу слоях.
Деформация сдвига жидкости — проскальзывание одного слоя жидкости относительно другого.
В идеальных жидкостях и газах эта деформация проходит без трения и не требует затраты работы внешней силы.
В реальных жидкостях и газах деформация сопровождается затратами энергии на преодоление сил трения
Вязкость— свойство жидкостей оказывать сопротивление сдвигу.
Количественно вязкость может быть получена из закона внутреннего трения Ньютона.
 ????=±???? ????????, где
????=±???? ????????, где????????
???? — касательное напряжение между слоями (сила трения, отнесенная к единице площади соприкосновения слоев [Н⁄м2];
???? — динамическая вязкость [Па⋅с]
????????

????????
— градиент скорости
Динамическая вязкость

 ???? = ???? ???????? [Па⋅с] — СИ; 1 Пуаз = [ г ] — СГС
???? = ???? ???????? [Па⋅с] — СИ; 1 Пуаз = [ г ] — СГС???????? см⋅с
Кинематическая вязкость


 ???? = ???? [м2] — СИ; 1 Стокс = [см2] — СГС
???? = ???? [м2] — СИ; 1 Стокс = [см2] — СГС???? с с
Режимы течения жидкости
Ламинарныйрежим— режим течения жидкости, при котором частицы движутся параллельно друг другу в направлении общего течения, при этом истинные скорости движения частиц на разном удалении от стенок трубопровода различны, в потоке имеет место слоистый характер движения жидкости, где каждый из бесконечного множества слоев объединяет частицы с одинаковой скоростью.
Турбулентныйрежим— режим течения жидкости, при котором наряду с общим продольным направлением перемещения потока частицы начнут совершать движения в поперечном направлении, описывая сложные траектории в потоке.
Количественной мерой режима движения жидкости является число Рейнольдса Re. Зависит от расхода или средней скорости течения жидкости, кинематической вязкости и поперечных размеров потока.
Re =2320 — Критическое значение. При Re
Расчетные формулы
-
Площадь поперечного сечения трубы
 ???? = ????????2 м, где d — диаметр трубы, м
???? = ????????2 м, где d — диаметр трубы, м4
-
Скорость течения потока жидкости
 ???? = ????;м/с, где ???? — расход жидкости м3; ????— площадь поперечного сечения трубы.
???? = ????;м/с, где ???? — расход жидкости м3; ????— площадь поперечного сечения трубы.????
-
Число Рейнольдса
???????? = ????????, где ???? — скорость течения потока жидкости м/с; d — диаметр трубы м; ???? —
????
кинематическая вязкость воды, м2/с.
-
Кинематическая вязкость воды при атмосферном давлении
 ???? = 0,0178
???? = 0,01781+0,0337????+0?000221????2
·10−4 , м2/с, t — средняя температура среды, °C
-
Соотношение средней и максимальной скоростей в турбулентном режиме
1
????????38
???? =

1,64
Таблица результатов измерений и расчетов
| № | d, м | f,м2 | Q,л | w,м/с | t, ℃ | ν, м2/с | Re | Режим движения жидкости |
| 1 | 0,012 | 1,13·10−4 | 0,1 | 0,0148 | 20 | 1,009·10−6 | 175 | Ламинарный |
| 2 | 0,012 | 1,13·10−4 | 0,6 | 0,089 | 20 | 1,009·10−6 | 1051 | Ламинарный |
| 3 | 0,012 | 1,13·10−4 | 1,5 | 0,221 | 20 | 1,009·10−6 | 2628 | Переходный |
| 4 | 0,012 | 1,13·10−4 | 4,3 | 0,634 | 20 | 1,009·10−6 | 7536 | Переходный |
| 5 | 0,012 | 1,13·10−4 | 4,4 | 0,649 | 20 | 1,009·10−6 | 7711 | Переходный |
| 6 | 0,012 | 1,13·10−4 | 5,1 | 0,752 | 20 | 1,009·10−6 | 8938 | Переходный |
| 7 | 0,012 | 1,13·10−4 | 5,8 | 0,855 | 20 | 1,009·10−6 | 10165 | Турбулентный |
| 8 | 0,012 | 1,13·10−4 | 6,9 | 1,017 | 20 | 1,009·10−6 | 12093 | Турбулентный |
| 9 | 0,012 | 1,13·10−4 | 7,9 | 1,165 | 20 | 1,009·10−6 | 13845 | Турбулентный |
| 10 | 0,012 | 1,13·10−4 | 8,5 | 1,253 | 20 | 1,009·10−6 | 14897 | Турбулентный |
| 11 | 0,012 | 1,13·10−4 | 8,8 | 1,297 | 20 | 1,009·10−6 | 15423 | Турбулентный |
| 12 | 0,012 | 1,13·10−4 | 9,3 | 1,372 | 20 | 1,009·10−6 | 16298 | Турбулентный |
| 13 | 0,012 | 1,13·10−4 | 9,4 | 1,386 | 20 | 1,009·10−6 | 16474 | Турбулентный |
| 14 | 0,012 | 1,13·10−4 | 9,5 | 1,401 | 20 | 1,009·10−6 | 16649 | Турбулентный |
| 15 | 0,012 | 1,13·10−4 | 9,7 | 1,431 | 20 | 1,009·10−6 | 17000 | Турбулентный |
| 16 | 0,012 | 1,13·10−4 | 10,2 | 1,504 | 20 | 1,009·10−6 | 17876 | Турбулентный |
| 17 | 0,012 | 1,13·10−4 | 10,7 | 1,578 | 20 | 1,009·10−6 | 18752 | Турбулентный |
| 18 | 0,012 | 1,13·10−4 | 11,1 | 1,637 | 20 | 1,009·10−6 | 19453 | Турбулентный |
(Таблица1)
Примеры расчетов для таблицы №1 значения №4

 ???? = ????????2 = 3,14·0,0122 =
???? = ????????2 = 3,14·0,0122 =1,13·10
−4 м;
4 4
 ???? 4,3·10−3
???? 4,3·10−3 ???? = =
???? = =????
1,13·10−4·60 = 0,634 м/с
 ???? = 0,0178
???? = 0,01781+0,0337·20+0?000221·202
· 10−4= 1,009·10−6, м2/с,
???????? =
???????? =
 ????
????0,634·0,0122

=
1,009·10−6 7536
На основе данных таблицы №1 были рассчитаны следующие значения:
| № | Lg(Re) | ω | № | Lg(Re) | ω |
| 1 | 2,24 | 0,50 | 10 | 4,17 | 0,79 |
| 2 | 3,02 | 0,50 | 11 | 4,19 | 0,79 |
| 3 | 3,42 | 0,75 | 12 | 4,21 | 0,79 |
| 4 | 3,88 | 0,77 | 13 | 4,22 | 0,79 |
| 5 | 3,89 | 0,77 | 14 | 4,22 | 0,79 |
| 6 | 3,95 | 0,77 | 15 | 4,23 | 0,79 |
| 7 | 4,01 | 0,78 | 16 | 4,25 | 0,79 |
| 8 | 4,08 | 0,78 | 17 | 4,27 | 0,79 |
| 9 | 4,14 | 0,78 | 18 | 4,29 | 0,79 |
(Таблица №2)
Пример расчета для таблицы №2 значения №4
???? =
1
????????38
 =
=1,64
1
753638

1,64
= 0,77
ω
Графическая обработка данных
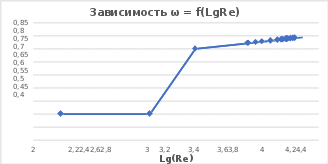 На основе таблицы №2 построена зависимость соотношения средней и максимальной скоростей жидкости от LgRe
На основе таблицы №2 построена зависимость соотношения средней и максимальной скоростей жидкости от LgReВывод: В ходе лабораторной работы были изучены режимы течения жидкостей. Было установлено, что режимы течения жидкостей зависит от числа Рейнольдса, которое, в свою очередь, зависит от скорости течения жидкости, диаметра поперечного сечения потока и кинематической вязкости жидкости. Также на практике было установлено, что изменяя расход жидкости, скорость потока также изменяется: при постоянном значении площади поперечного сечения трубы чем больше скорость потока, тем выше его скорость. На основе полученных данных была построена зависимость соотношения средней и максимальной скоростей жидкости от LgRe, при разных режимах течения жидкостей, полученных экспериментально.