Добавлен: 20.10.2018
Просмотров: 556
Скачиваний: 12
Задание № 10. Решение задач в Microsoft Excel: Встроенный модуль «Поиск решения»
1. Ознакомьтесь с задачей линейного программирования, представленной ниже.
Задача 1. Для приготовления смолы необходимо составить смесь, пользуясь набором из трех компонентов: A, B, C, ресурсы которых ограничены соответственно 20, 25 и 10 кг в расчете на одну загрузку. При этом требуется, чтобы смесь содержала необходимое количество химических добавок D (не менее 20 г), E (не менее 2000 г), F (не менее 100 г) и при этом оказалась наиболее выгодной по себестоимости.
Следующая таблица характеризует содержание химических добавок D, E и F в одном килограмме каждого компонента и себестоимость компонентов A, B и C.
|
Виды компонентов |
Содержание химических добавок, г |
Себестоимость1 кг компонента |
||
|
D |
E |
F |
|
|
A |
0,5 |
40 |
5 |
2 |
|
B |
0,2 |
10 |
4 |
1 |
|
C |
1,0 |
200 |
3 |
4 |
Для составления математической модели обозначим через x1, x2 и x3 соответственно количество килограммов компонента A, компонента B и компонента C, которые составляют искомую смесь. Тогда на основании условий задачи данные переменные должны удовлетворять следующим ограничительным условиям:
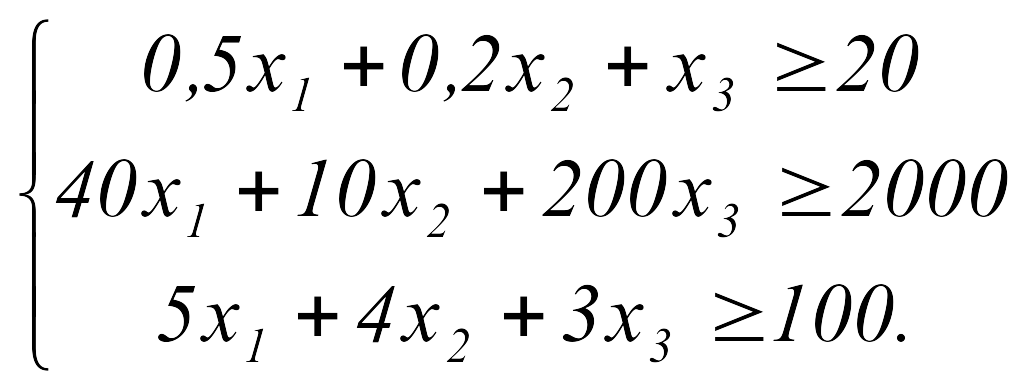
Введем ограничения по ресурсам согласно условию:
![]()
Кроме того, переменные должны быть неотрицательными, т.е.
![]()
Очевидно, существует множество решений системы неравенств. Необходимо выбрать тот состав смеси, который обладает наименьшей себестоимостью, т.е.
![]()
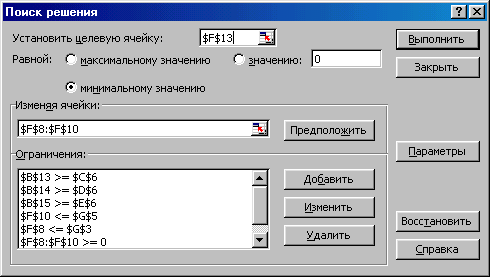
2. Рассмотрите модуль «Поиск решения» (Сервис Поиск решения). (При отсутствии модуля его необходимо подключить при помощи меню «Сервис Надстройки».)
В окно «Установить целевую ячейку» вводится адрес целевой функции, которая стремится к какому-либо значению (в нашем случае – к минимальному). В окно «Изменяя ячейки» вводятся адреса ячеек, которые отведены под искомые значения переменных. В окно «Ограничения» добавляются все необходимые условия.
Обратите внимание
на возможность изменения параметров
поиска решений
![]() в указанном модуле.
в указанном модуле.
3. Решите в Excel при помощи модуля «Поиск решения» представленную выше задачу:
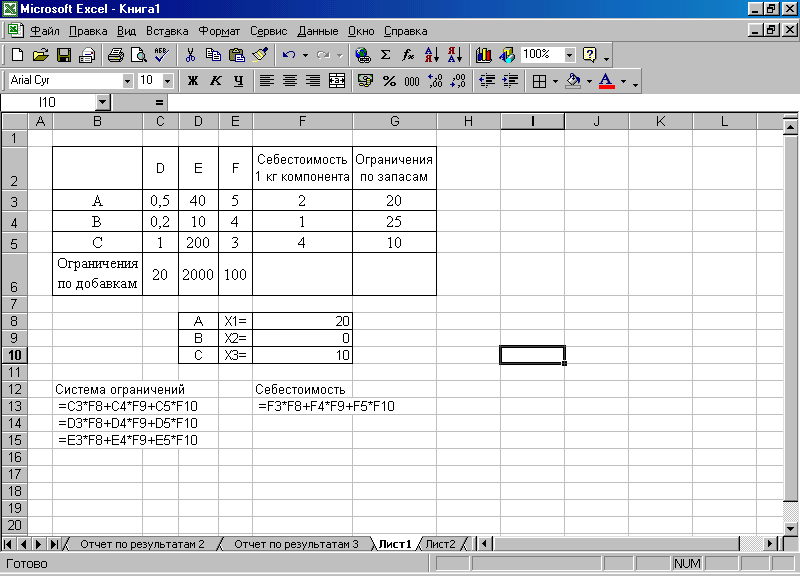
4. Самостоятельно в Excel решите следующую задачу.
Задача 2. Для производства двух видов изделий X и Y предприятие использует три вида сырья. Известен расход сырья каждого вида на изготовление единицы продукции вида X: 1,1; 2,3; 4,9 кг соответственно, и продукции вида Y: 0,8; 5,3; 2 кг. Общий запас сырья составляет соответственно 15; 6; 8 тонн. Прибыль от реализации продукции вида X – 180 рублей, вида Y – 110 рублей. Составить оптимальный план производства изделий, обеспечивающий максимальную прибыль.