Файл: 2 Нет ответа Текст вопроса к теоретикомножественным операциям не относится операция Выберите один ответ разности объединения деления пересечения Отзыв Правильный ответ деления Вопрос 3.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 74
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
антисимметричность транзитивность рефлексивность симметричность антирефлексивностьОтзыв
Правильный ответ: антирефлексивность, симметричность
Вопрос 4
Нет ответа
Текст вопроса
Свойством коммутативности обладает операция
Выберите один или несколько ответов:
симметрическая разность множеств разность множеств пересечение множеств объединение множествОтзыв
Правильный ответ: объединение множеств, пересечение множеств, симметрическая разность множеств
Вопрос 5
Нет ответа
Текст вопроса
Пусть А - непустое множество всех учеников школы, В - множество учеников пятых классов этой школы, С - множество учеников седьмых классов этой школы. Тогда ложным является утверждение
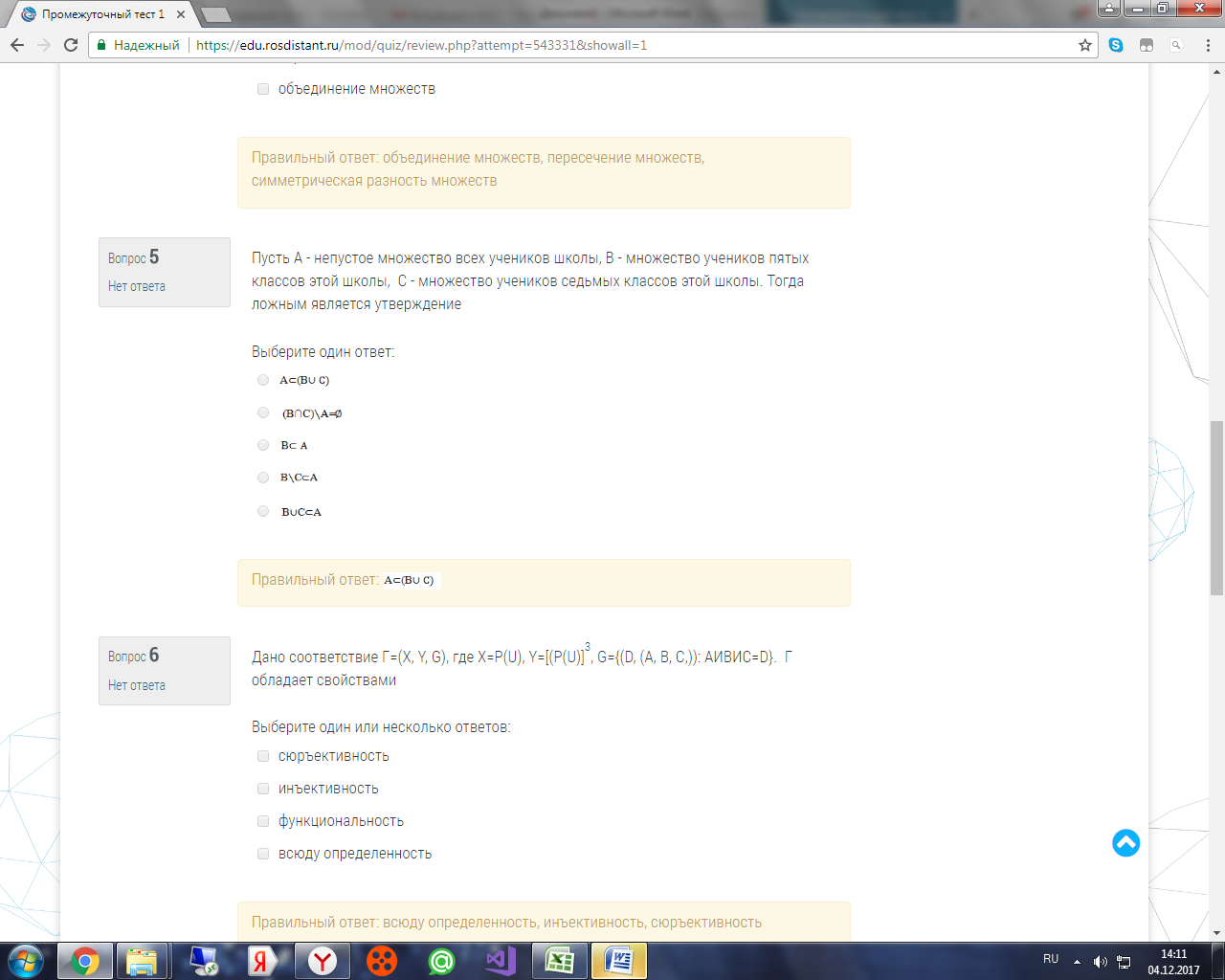
Вопрос 6
Нет ответа
Текст вопроса
Дано соответствие Г=(X, Y, G), где X=P(U), Y=[(P(U)]3, G={(D, (A, B, C,)): AИBИC=D}. Г обладает свойствами
Выберите один или несколько ответов:
сюръективность инъективность функциональность всюду определенностьОтзыв
Правильный ответ: всюду определенность, инъективность, сюръективность
Вопрос 7
Нет ответа
Текст вопроса
Дано соответствие Г=(X, Y, G), где X= [1, 3], Y= R+ , G={(x,y): (x-2)2+(y-2)2Ј1}. Г обладает свойствами
Выберите один или несколько ответов:
сюръективность всюду определенность
функциональность
инъективностьОтзыв
Правильный ответ: всюду определенность
Вопрос 8
Нет ответа
Текст вопроса
Выбрать множество С, если А = {1;2;3}; В = {2;3;4;}; С = {1;2;3;4}.
Вопрос 9
Нет ответа
Текст вопроса
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 5}, B={2,4,5,6}. Найти .
Выберите один ответ:
{1,2,4,5,} {x| x < 7, } {1,2,3,4,5,6} {1,3}Отзыв
Правильный ответ: {1,2,3,4,5,6}
Вопрос 10
Нет ответа
Текст вопроса
Укажите верное соотношение.
Нет ответа
Текст вопроса
Отношение , где A= N, x y Ы x и y имеют одинаковый остаток от деления на 3, обладает свойствами
Выберите один или несколько ответов:
антирефлексивность транзитивность симметричность антисимметричность рефлексивностьОтзыв
Правильный ответ: рефлексивность, симметричность, транзитивность
Нет ответа
Текст вопроса
Дано соответствие Г=(X, Y, G), где X={a, b, c, d}, Y={1, 2, 3, 4, 5}, G={(a,3), (b,5), (c,4), (d,1)}. Г обладает свойствами
Выберите один или несколько ответов:
инъективность сюръективность всюду определенность функциональностьОтзыв
Правильный ответ: функциональность, инъективность
Вопрос 2
Нет ответа
Текст вопроса
Отношение , где A - множество окружностей на плоскости, x y Ы x касается y, обладает свойствами
Выберите один или несколько ответов:
антирефлексивность транзитивность симметричность рефлексивность антисимметричностьОтзыв
Правильный ответ: антирефлексивность, симметричность
Вопрос 3
Нет ответа
Текст вопроса
Отношение , где A= [0, 2], x y Ы x + y<1, обладает свойством
Выберите один ответ:
рефлексивность антисимметричность транзитивность антирефлексивность симметричностьОтзыв
Правильный ответ: симметричность
Отношение , где A= [0, 4], x y Ы x >2y+1, обладает свойствами
Выберите один или несколько ответов:
антирефлексивность транзитивность антисимметричность симметричность рефлексивностьОтзыв
Правильный ответ: антирефлексивность, антисимметричность, транзитивность
Дано соответствие Г=(X, Y, G), где X={Окружности на плоскости}, Y={Прямые на плоскости}, G={(окружность, касательная к окружности)}. Г обладает свойствами
Выберите один или несколько ответов:
сюръективность инъективность функциональность всюду определенность Отзыв
Правильный ответ: всюду определенность, сюръективность
Дано соответствие Г=(X, Y, G), где X=R, Y={Непрерывные на [a, b] функции}, G={(max f(x), f(x))}. Г обладает свойствами
Выберите один или несколько ответов:
сюръективность функциональность инъективность всюду определенностьОтзыв
Правильный ответ: всюду определенность, сюръективность
Вопрос 8
Нет ответа
Текст вопроса
Дано соответствие Г=(X, Y, G), где X= [1, 3], Y= R+ , G={(x,y): (x-2)2+(y-2)2Ј1}. Г обладает свойствами
Выберите один или несколько ответов:
сюръективность функциональность всюду определенность инъективностьОтзыв
Правильный ответ: всюду определенность
Дано соответствие Г=(X, Y, G), где X={a, b, c}, Y={1, 2, 3, 4, 5}, G={(a,2), (b,1), (c,5), (a,3)}. Г обладает свойствами
Выберите один или несколько ответов:
всюду определенность сюръективность функциональность инъективностьОтзыв
Правильный ответ: всюду определенность, инъективность
Выберите один или несколько ответов:
всюду определенность инъективность функциональность сюръективностьОтзыв
Правильный ответ: всюду определенность, сюръективность
Вопрос 2
Нет ответа
Текст вопроса
Отношение , где A= N, x y Ы x и y имеют одинаковый остаток от деления на 3, обладает свойствами
Выберите один или несколько ответов:
транзитивность антирефлексивность рефлексивность симметричность
антисимметричностьОтзыв
Правильный ответ: рефлексивность, симметричность, транзитивность
Вопрос 3
Нет ответа
Текст вопроса
Дано универсальное множество U={1,2,3,4,5,6,7} и в нем подмножества A={x| x < 5}, B={2,4,5,6}. Найти .
Выберите один ответ:
{1,3} {x| x < 7, } {1,2,3,4,5,6} {1,2,4,5,}Отзыв
Правильный ответ: {1,2,3,4,5,6}
Вопрос 4
Нет ответа
Текст вопроса
Пусть А - непустое множество всех учеников школы, В - множество учеников пятых классов этой школы, С - множество учеников седьмых классов этой школы. Тогда ложным является утверждение
Выберите один ответ:
Отзыв
Правильный ответ:
Вопрос 5
Нет ответа
Текст вопроса
А = {1;2}, В = {2;3}. Найти ВхА .
Выберите один ответ:
{(1;2);(1;3);(2;2);(2;3)} {(2;3);(2;2);(3;2);(3;3)} {(1;2);(1;1);(2;1);(2;2)} {(2;1);(2;2);(3;1);(3;2)}Отзыв
Правильный ответ: {(2;1);(2;2);(3;1);(3;2)}
Вопрос 6
Нет ответа
Текст вопроса
Отношение , где A= P(U), U – множество точек плоскости, А В Ы А З В =Ж, обладает свойством
Выберите один ответ:
транзитивность антисимметричность антирефлексивность симметричность рефлексивностьОтзыв
Правильный ответ: симметричность
Вопрос 7
Нет ответа
Текст вопроса
Отношение , где A= [0, 4], x y Ы x >2y+1, обладает свойствами