ҚАЗАҚСТАН РЕСПУБЛИКАСЫ БІЛІМ ЖӘНЕ ҒЫЛЫМ МИНИСТІРЛІГІҒЫЛЫМИ ЖОБАНЫҢ ТАҚЫРЫБЫ:Бағыты: Тақырыбы: «Теңдеулердің түрлері және оларды шешу жолдары»Оқушының толық аты:Ғылыми жетекші:Сынып:Бағыты:Қаласы:2022-2023 оқу жылыЭССЕҚазіргі әлемде математика маңызды рөл атқарады, ол бізді қоршап тұрған көптеген құбылыстарды түсінуге және түсіндіруге көмектеседі. Математикадағы негізгі тақырыптардың бірі-теңдеулер мен оларды шешу әдістерін зерттеу. Бұл эсседе біз теңдеулердің әртүрлі түрлерін және оларды шешу жолдарын қарастырамыз.Теңдеу-белгісіз мәндер болатын математикалық өрнек. Теңдеудің шешімі-берілген теңдікті қанағаттандыратын мәндерді іздеу. Теңдеулердің бірнеше түрі бар және олардың әрқайсысы тиісті шешім әдісін қолдануды талап етеді.Жұмыстың теориялық бөлімінде мен теңдеудің түрлерімен және оларды шешудің әртүрлі әдістерімен таныстым. Бұл менің ойлау көкжиегімді дамытты және математиканы тереңірек түсінуге деген ынта-жігерімді арттырды. Теңдеулерді классификациялауды үйрену арқылы алдағы уақыттағы есеп шығаруға деген қабілетімді арттырдым.Жұмыстың практикалық бөлігінде мен әр түрдегі теңдеулердің бірнеше мысалын қарастырдым және шештім. Бұл маған дұрыс шешім әдісін қалай таңдауға және оны іс жүзінде қолдануға болатындығын жақсы түсінуге көмектесті. Практикалық мысалдар теориялық білімді нығайтуға және теңдеулерді шешу дағдыларын дамытуға көмектесті.Қорытындылай келе, теңдеулердің әртүрлі түрлерін және оларды шешу әдістерін зерттеу математикалық білім берудегі маңызды кезең болып табылады. Теңдеулерді шешудің негізгі принциптері мен әдістерін түсіну логикалық ойлау мен аналитикалық дағдыларды дамытуға көмектеседі. Бұл жұмыс сізге теңдеулер туралы білімді тереңдетуге және оны математика мәселелерді шешудің ажырамас бөлігі болып табылатын әртүрлі жағдайларда қолдануға көмектеседі деп үміттенемін.АННОТАЦИЯБұл ғылыми жұмыс теңдеулердің әртүрлі түрлерін және оларды шешу әдістерін зерттеуге арналған. Жұмыста теңдеулерге, олардың түрлеріне байланысты негізгі ұғымдарға шолу жасалады, сонымен қатар сызықтық теңдеулерді, квадрат теңдеулерді және рационал теңдеулерді шешу әдістері ұсынылады.Жұмыстың теориялық бөлігі теңдеулердің әр түрінің анықтамалары мен мысалдарын қамтиды, сонымен қатар тиісті шешу әдістерін сипаттайды. Сызықтық теңдеулер, квадрат теңдеулер, рационал теңдеулер және теңдеулер жүйесі егжей-тегжейлі қарастырылып, оқушыға әрқайсысы туралы толық түсінік береді.

---

Жұмыстың практикалық бөлігі сызықтық теңдеулерді, квадрат теңдеулерді, рационал теңдеулерді және теңдеулер жүйесін қамтитын бірқатар практикалық мысалдарды қамтиды. Әрбір мысал есепті қоюдың, шешудің тиісті әдісін таңдаудың және теңдеулерді кейіннен практикалық шешудің егжей-тегжейлі сипаттамасымен бірге жүреді.Зерттеу нәтижесінде жұмысты қорытындылайтын негізгі қорытындылар алынды. Жұмыс оқушыға теңдеулердің түрлерін, олардың ерекшеліктерін және оларды қалай шешуге болатындығын жақсы түсінуге көмектеседі. Бұл практикалық құндылықты білдіреді, өйткені студент алған білімін теңдеулермен жұмыс істеуді қажет ететін нақты мәселелерді шешу үшін қолдана алады.Барлық пайдаланылған әдебиеттер, соның ішінде оқулықтар, мақалалар және интернет-ресурстар пайдаланылған әдебиеттер тізімінде көрсетіледі, бұл оқырманға жұмыста пайдаланылған ақпарат көздерімен танысуға мүмкіндік береді.АННОТАЦИЯДанная научная работа посвящена изучению различных видов уравнений и методов их решения. В работе представлен обзор основных понятий, связанных с уравнениями, их видами, а также предложены методы решения линейных уравнений, квадратных уравнений и рациональных уравнений.Теоретическая часть работы содержит определения и примеры каждого вида уравнений, а также описывает соответствующие методы решения. Линейные уравнения, квадратные уравнения и рациональные уравнений рассматриваются в деталях, предоставляя учащемуся полное представление о каждом из них.Практическая часть работы содержит ряд практических примеров, включающих линейные уравнения, квадратные уравнения и рациональные уравнений. Каждый пример сопровождается подробным описанием постановки задачи, выбора соответствующего метода решения и последующего практического решения уравнений.В результате исследования были получены основные выводы, подводящие итоги работы. Работа помогает учащемуся лучше понять виды уравнений, их особенности и способы их решения. Она представляет практическую ценность, так как учащийся может применить полученные знания для решения реальных задач

---

, в которых требуется работа с уравнениями.

Вся используемая литература, включая учебники, статьи и интернет-ресурсы, указывается в списке использованной литературы, что позволяет читателю ознакомиться с источниками информации, использованными в работе.


ANNOTATION
This scientific work is devoted to the study of various types of equations and methods of their solution. The paper presents an overview of the basic concepts related to equations, their types, and also suggests methods for solving linear equations, quadratic equations and rational equations.

The theoretical part of the work contains definitions and examples of each type of equations, as well as describes the corresponding methods of solution. Linear equations, quadratic equations and rational equations are considered in detail, providing the student with a complete understanding of each of them.

The practical part of the work contains a number of practical examples, including linear equations, quadratic equations and srationalequations. Each example is accompanied by a detailed description of the problem statement, the choice of the appropriate solution method and the subsequent practical solution of the equations.

As a result of the study, the main conclusions summarizing the work were obtained. The work helps the student to better understand the types of equations, their features and ways to solve them. It is of practical value, since the student can apply the acquired knowledge to solve real problems in which work with equations is required.

All the literature used, including textbooks, articles and Internet resources, is indicated in the list of references, which allows the reader to familiarize himself with the sources of information used in the work.


ҒЫЛЫМИ ЖОБАНЫҢ МАЗМҰНЫ


І. КІРІСПЕ.............................................................................................................

ІІ. НЕГІЗГІ БӨЛІМ..............................................................................................

2.1. Теңдеу ұғымы....................................................................................................

2.2. Теңдеу түрлері мен шешу жолдары...............................................................

Ⅲ. ПРАКТИКАЛЫҚ БӨЛІМ………………………………………………..

3.1. Квадрат теңдеулердің практикалық мысалдары…………………………….

3.3. Рационал теңдеулердің практикалық мысалдары………………………...

ІҮ. ҚОРЫТЫНДЫ...............................................................................................

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ.......................................................

І. КІРІСПЕ
Алгебралық теңдеулер алгебра мен жалпы математиканы зерттеудің негізгі тақырыптарының бірі болып табылады. Олар берілген шарттар мен амалдар арқылы белгісіз мән ізделетін математикалық өрнектер. Алгебралық теңдеулердің түрлерін және оларды шешу жолдарын түсіну математикалық және логикалық ойды дамытудың негізі болып табылады.

Жобаның мақсаты: Теңдеулердің түрлерімен танысу және оларды шешу жолдарын зерттеу.

Таңдалған тақырыптың өзектілігі: Теңдеулер математиканың негізі болып табылады және білімнің көптеген салаларында қолданылады. Теңдеулердің әртүрлі түрлерін және оларды шешу әдістерін түсіну оқушылардың математикалық сауаттылығын дамытуға мүмкіндік береді және математиканы одан әрі зерттеу үшін негізгі құзыреттілікті қамтамасыз етеді.

---

Зерттеу нысаны: Математикалық теңдеулер.Зерттеу пәні: Әртүрлі типтегі математикалық теңдеулер және әдістер.Гипотеза: Теңдеулердің әртүрлі түрлерін және оларды шешу әдістерін үйрену математикалық теңдеулердің негізгі принциптерін жақсы түсінуге және олардың шешімдерін табу үшін тиісті әдістерді тиімді қолдануды үйренуге көмектеседі.Міндеттері:

1. 
   Теңдеу ұғымымен танысу.
   
2. 
   Теңдеудің түрлерін және олардың шешу жолдарын көрсету.
   
3. 
   Теңдеулердің шешу жолдарын практикалық мысалдарда қолдану .
   

Зерттеу әдістері:

1. 
   Оқулықтар мен оқу материалдарын талдау;
   
2. 
   Интернеттен және басқа көздерден ақпарат іздеу;
   
3. 
   Практикалық мысалдарды шешу;
   
4. 
   Жетекшімен кеңесу.
   

ІІ. НЕГІЗГІ БӨЛІМ2.1. Теңдеу ұғымыТеңдеу - бұл белгісіз шамалар мен амалдар болатын математикалық өрнек, олардың көмегімен белгісіз шамаларды табуға болады. Ол екі алгебралық өрнектің теңдігін бекітеді және теңдік белгісін (=) қолдана отырып жазылады.Теңдеудің маңызды элементтері:

• 
  Белгісіз шамалар: бұл табу немесе анықтау қажет мәндер. Әдетте x, y немесе z сияқты латын әріптермен белгіленеді.
  
• 
  Коэффициенттер: бұл белгісіз шамаларға көбейтілетін сандар. Олар сандармен немесе сандық мәндері бар грек немесе латын әріптермен ұсынылуы мүмкін.
  
• 
  Амалдар: теңдеулерде квадраттау, түбір алу, қосу, азайту, көбейту және бөлу сияқты арифметикалық амалдар жиі қолданылады.(1-cурет)
  

1-суретКүнделікті өмірдегі теңдеулердің мысалдары:Егер x адамның жасын білдірсе, онда "x + 5 = 20" теңдеуі белгісіз x жасына 5 жасты қосқан кезде 20 жас шығатынын білдіреді. Бұл теңдеудің шешімі x = 15 болады.Егер массасы 3 кг жәшікке массасы белгісіз x кг жәшікті таразыға қосып өлшегендегі салмағы 7 кг жәшікке тең екендігі белгілі болса, онда бастапқыда белгісіз жәшіктің салмағын теңдеу арқылы анықтап алуға болады. Ізделінді жәшіктің массасы x=4 кг болады. 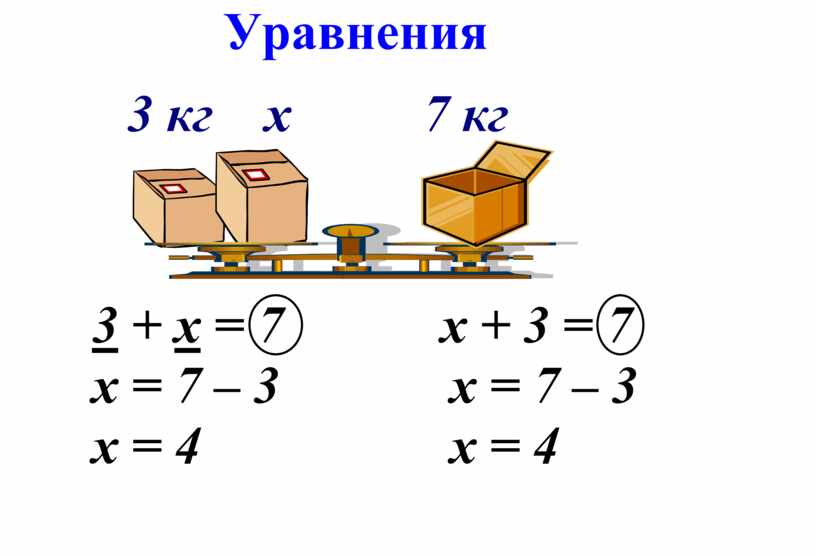(2-cурет)2-суретТеңдеулерді зерттеудің негізгі мақсаты шешімдерді, яғни теңдеу дұрыс болатын белгісіз шамалардың мәндерін табу болып табылады. Теңдеулерді шешу үшін алгебралық түрлендірулер, факторизация, алмастыру және графикалық әдіс сияқты әртүрлі әдістер қолданылады.

---

Теңдеудің бір, бірнеше немесе тіпті шексіз шешімдері болуы мүмкін екенін және теңдеуді қанағаттандыратын мәндер болмаса, шешілмейтінін түсіну маңызды.Теңдеу ұғымын түсіну теңдеулердің әртүрлі түрлерін және оларды шешу әдістерін зерттеудің маңызды қадамы болып табылады, олар жұмыстың келесі бөлімдерінде қарастырылады.2.2. Теңдеу түрлері мен шешу жолдары2.2.1. Сызықтық теңдеулер.Сызықтық теңдеу-бұл айнымалылардың дәрежелері бірінші дәрежеден аспайтын және айнымалылардың көбейтінділері жоқ теңдеу. Сызықтық теңдеудің жалпы көрінісін келесідей жазуға болады:ax + b = 0,мұндағы a және b - коэффициенттер, x – айнымалы [5].Сызықтық теңдеулердің мысалдары:а) 2x + 3 = 0 - сызықтық теңдеу, өйткені x айнымалысының дәрежесі 1-ге тең.б) 4y - 5 = 0-сонымен қатар сызықтық теңдеу болып табылады, өйткені y айнымалысының дәрежесі 1-ге тең.в) 3z + 2w = 7 - екі z және w айнымалысы бар сызықтық теңдеулер жүйесі. Сызықтық теңдеулерді шешу әдістері:а) Таңдау әдісі: бұл әдіспен біз айнымалының табылған мәнін теңдеуге ауыстырамыз және оның дұрыстығын тексереміз.Мысал:2x + 3 = 0 теңдеуін қарастырыңыз. x= -1 ауыстырайық:2(-1) + 3 = 0-2 + 3 = 01 = 0 (дұрыс емес теңдік)Демек, x = -1 теңдеудің түбірі емес.б) Канондық түрге келтіру әдісі: бұл әдіспен теңдеуді x = c түрінде болатындай етіп түрлендіреміз, мұндағы c - тұрақты.Мысал:2x + 3 = 0 теңдеуін қарастырайық. Оны канондық түрге келтірейік:2x = -3x = -1,5Біз x = -1,5 шешімін аламыз.в) Графитік әдіс: бұл әдіспен біз теңдеудің графигін құрамыз және графиктің теңдеудің түбіріне сәйкес келетін абсцисса осімен (x осі) қиылысу нүктесін анықтаймыз [2].Мысал:2x + 3 = 0 теңдеуін қарасайық. Оның графигін сызамыз:Ол үшін екі ерікті нүктені таңдаймыз (мысалы, x = 0 және x = -2) және сәйкес y мәндерін табамыз:x = 0 үшін: y = 2 (0) + 3 = 3x = -2 үшін: y = 2 (-2) + 3 = -1Содан кейін алынған нүктелерді сызықпен қосу арқылы график құрамыз. 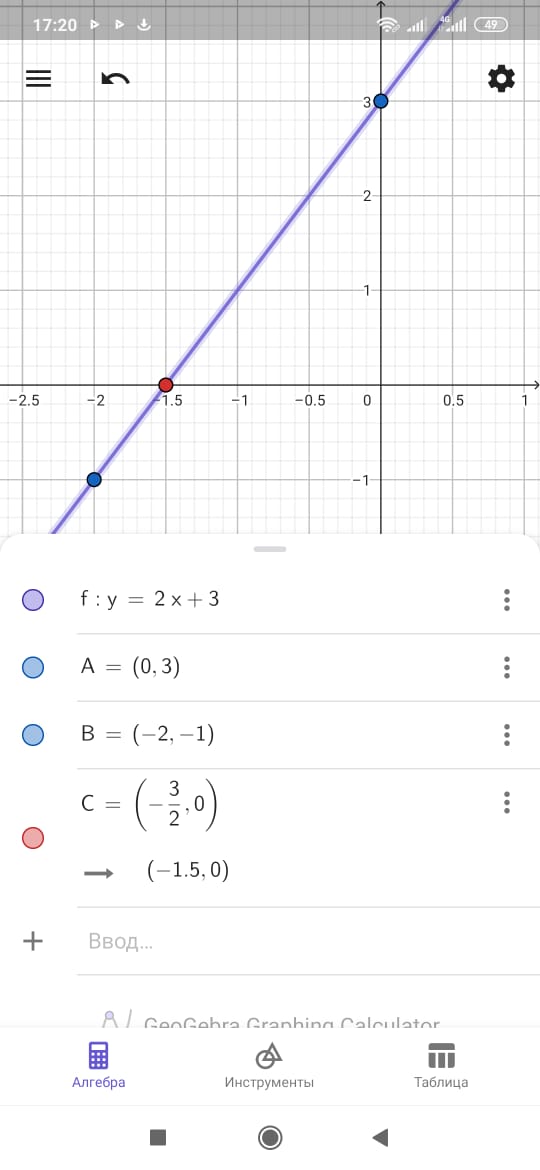График х осін (-1,5, 0) нүктесінде қиып өтетін түзу сызық болады.Демек, 2x + 3 = 0: x = -1,5 теңдеуінің шешімі.г) Қысқарту әдісі: бұл әдіспен біз шешімді алу үшін алгебра мен арифметиканың қасиеттерін қолдана отырып теңдеуді түрлендіреміз [3].Мысал:2x + 3 = 0 теңдеуін қарастырайық. Теңдіктің екі жағына да -3 санын қосамыз. Біз оны келесідей түрлендіреміз:2x = -3x = -1,5Осыдан, x = -1,5 шешімін аламыз.

---

Смотрите также файлы

• В современном строительстве 60% по объему составляет возведение зданий и сооружений из монолитных железобетонных конструкций.docx

• Джордж Беркли.docx

• О допуске лиц, обучающихся по образовательным программам высшего образования, к занятию педагогической деятельностью по общеобразовательным программам.pdf

• Основы оперативного планирования и управления материального потока в производстве..docx

• Практических заданий по дисциплине развитие отраслевых комплексов крупного города.docx