Теңдеудің берілгеніне байланысты әртүрлі әдістерді қолдануға болады. Есеп шығару барысында теңдеудің берілгеніне қарай әдіс таңдалынады.

2.2.2. Квадраттық теңдеулер.

Квадраттық теңдеу – теңдеуге айнымалы дәрежесі 2 ге тең түрінде кездесетін теңдеу. Квадраттық теңдеудің жалпы түрі келесідей:

,

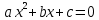мұндағы 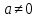[1].

Квадрат теңдеулердің мысалдары:

1. 
   ,
   
2. 
   ,
   
3. 
   .
   

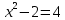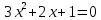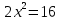Квадрат теңдеулерді шешу әдістері:

a) Дискриминант формуласы:

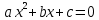квадрат теңдеуінің формуламен берілген екі түбірі бар:

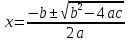(1)

мұндағы √ квадрат түбірді білдіреді. 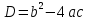дискриминанты теңдеудің қанша түбірі бар екенін және олардың сипатын анықтауға мүмкіндік береді:

Егер D > 0 болса, онда теңдеудің екі түрлі түбірі болады.

Егер D = 0 болса, онда теңдеудің бір түбірі болады (2 еселігі бар түбір).

Егер D < 0 болса, онда теңдеудің нақты түбірі болмайды (күрделі түбірі бар).[1]

b) Квадратты толықтыру әдісі: Квадрат теңдеу 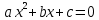келесідей канондық түрге келтіріледі:

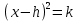, (2)

мұндағы h және k - квадратты толықтыру арқылы алынған тұрақтылар. Содан кейін квадрат түбірлердің қасиеттерін пайдаланып x мәндерін табуға болады.[3]

c) Графиктік әдіс: квадрат теңдеудің графигі - парабола. Теңдеудің шешімі параболаның x осімен қиылысу нүктелерін анықтаудан тұрады, бұл теңдеудің түбірлерін табуға мүмкіндік береді.

Мысалы, 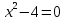теңдеуі түбірлерінің -2 және 2 болатынын график арқылы көрсетуге болады :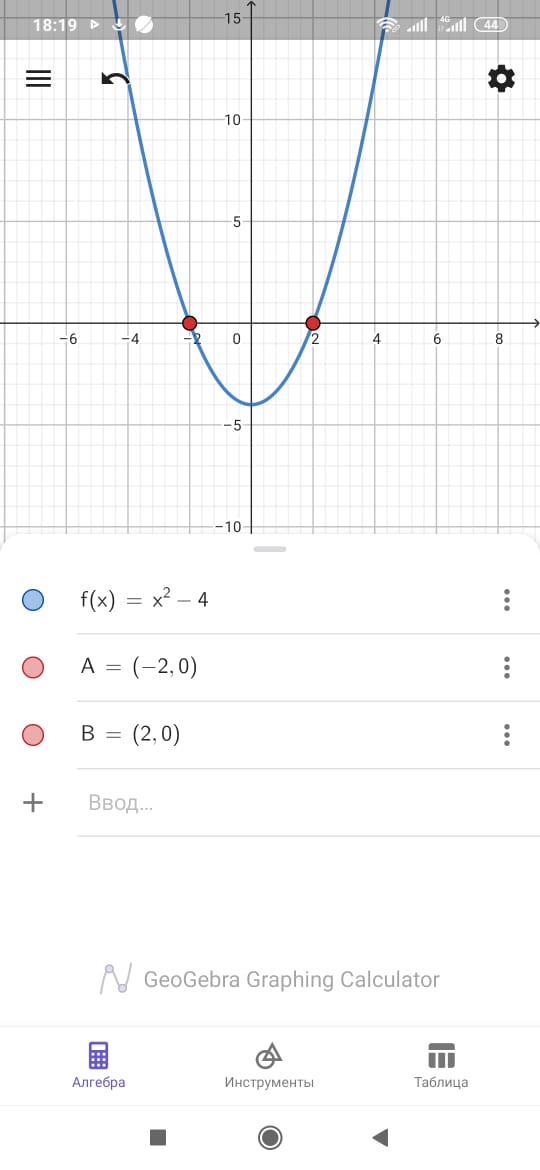



d) Факторизация: кейбір квадрат теңдеулерді көбейткішке жіктеуге болады, бұл теңдеудің түбірлерін әр факторды нөлге теңестіру арқылы табуға мүмкіндік береді.[1]

---

Квадрат теңдеулерді шешкен кезде ерекше жағдайларды ескеру қажет, мысалы, a = 0 немесе бір немесе одан да көп коэффициенттер нөлге тең болғанда.

Жұмыстың практикалық бөлігі оларды шешудің әртүрлі әдістері бар квадрат теңдеулердің мысалдарын, сондай-ақ x айнымалысының мәндерін табу үшін осы әдістерді қолдануды қажет ететін есептерді қамтиды.

2.2.3. Рационал теңдеулер.

Бөлшек рационал теңдеу - бұл рационал өрнектер, яғни айнымалылары бар бөлшек түріндегі теңдеу. Рационал теңдеудің жалпы көрінісі келесідей [3]:



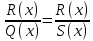
мұндағы P(x), Q(x), R(x), S(x) - x айнымалысы бар көпмүшелер, ал R(x)/S (X) - рационалды өрнек.

Рационалды теңдеулердің мысалдары [4]:

1. 
   ,
   
2. 
   ,
   
3. 
   .
   

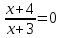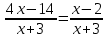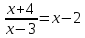Рационалды теңдеулерді шешу әдістері:

a) Ортақ бөлгіш әдісі: рационал теңдеулерді шешудің бір әдісі болып табылады. Ол теңдеудегі барлық бөлшектерді бір Бөлшекке біріктіру және алынған теңдеуді шешу үшін ортақ бөлгішке келтіруге негізделген.

c) Ортақ бөлгішке көбейту әдісі: теңдеудегі барлық бөлшектерді ортақ бөлгішке көбейту арқылы бөлшектің бөлімінен құтылуға және теңдеуді одан әрі жеңілдетуге негізделген.

д) Айнымалыны ауыстыру әдісі: бастапқы айнымалыны теңдеуді жеңілдетуге және оны қарапайым түрге келтіруге көмектесетін жаңа айнымалыға ауыстыруға негізделген.

Ⅲ. ПРАКТИКАЛЫҚ БӨЛІМ

3.1. Квадрат теңдеулердің практикалық мысалдары

Келесі квадраттық теңдеуді әртүрлі әдістермен шығарылуын қарастырайық:



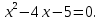
a) Дискриминант формуласы.

Берілген квадрат теңдеудің дискриминантын есептейміз:



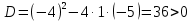
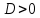жағдайы орындалды. Демек, квадрат теңдеудің әртүрлі екі түбірі болады. (1) формуласы бойынша теңдеудің түбірлерін есептейміз:

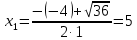және

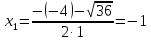
Теңдеудің түбірлері табылды. Олар 5 және -1.

в) Квадратты толықтыру әдісі.

Бұл әдіс бойынша берілген теңдеуді толық квадратқа яғни, (2) түріне келтіреміз:

---

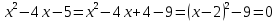
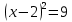
Теңдеу (2) түріне келді, енді оның түбірлерін есептейміз:

,

,

.

,

,

.

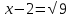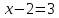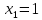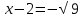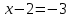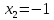Сонымен теңдеудің түбірлері табылды олар: 5 және -1.

С) Графиктік әдіс

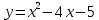функциясының графигін саламыз:

1. 
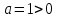   парабола тармағы жоғары қарайды.
   
2. 
   Дискриминант оң, парабола Ох осьімен екі нүктеде қиылысады.
   

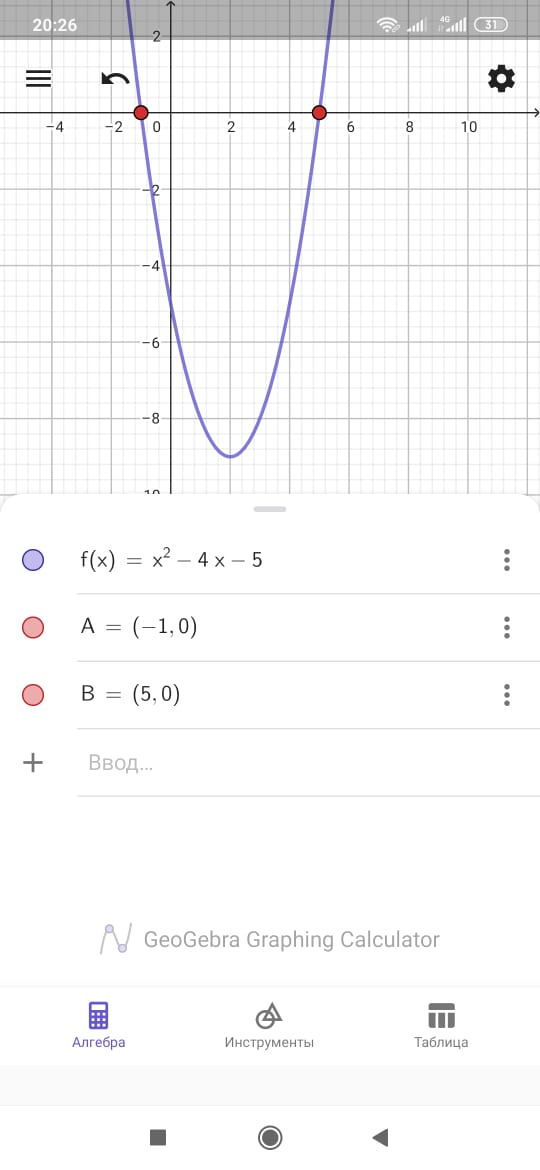
Қиылысу нүктелері (-1.0) және (5.0). Демек 5 және -1 бастапқы теңдеудің түбірлері болады.

д) Факторизация әдісі



Теңдеуді шешу үшін өрнегін көбейткіштерге жіктейміз:





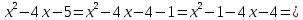
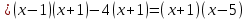
Пайда болған көбейткіштердің әрқайсысын нөлге теңестіріп, теңдеудің шешімін табамыз:





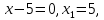
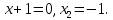
Теңдеудің түбірлері табылды. Олар 5 және -1.

Квадрат теңдеудің дербес жағдайлары:



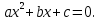
теңдеуі 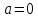болса, келесі түрдегі сызықтық теңдеуге айналады.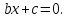



бұл теңдеудің шешімі сызықты теңдеуді шешу әдістерімен ізделінеді.

3.2. Рационалды теңдеулерді шешу мысалдары

Рационал теңдеуді шешкен кезде әр кезде әр түрлі әдіс қолданылатынын ескереміз.

---

Мысал 1. Келесі рационал теңдеуді қарастырайық:



Бұл теңдеуді шешпес бұрын, 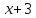өрнегінің нөл емес яғни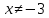

екенін ескереміз.

Теңдеуді шешу үшін ортақ бөлгішке көбейту әдісін қолдану тиімді. Теңдіктің екі жағын да ортақ бөлгіш 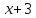ке көбейтіп, белгісізді cызықты теңдеуді шешудің канондық түрге келтіру әдісімен есептейміз: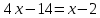







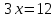
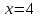
теңдеудің шешімі табылды, ол 4 ке тең.

Мысал 2. Келесі рационал теңдеуді қарастырайық:



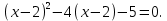
Бұл теңдеу жаңа айнымалы енгізу әдісімен шығарылады. Теңдеуге

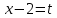
Айнымалысын енгізіп, жаңа айнымалыға қатысты теңдеу шешеміз:





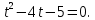
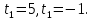
Енгізген айнымалыны теңдеудің мәндеріне теңестіріп, бастапқы теңдеудің шешімін табамыз:

,



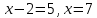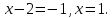
Бастапқы теңдеудің шешімдері табылды. Олар: 7 және 1.

ІҮ. ҚОРЫТЫНДЫ

Зерттеу барысында" теңдеулердің түрлері және оларды шешу әдістері " тақырыбында теңдеулердің негізгі түрлері. Теңдеулердің әр түрінің анықтамалары зерттелді, сонымен қатар күнделікті өмірден осы теңдеулерді қолдануға болатын мысалдар келтірілді.

Зерттеудің маңызды бөлігі теңдеулердің әр түрін шешу әдістері болды. Сызықтық теңдеулер үшін ауыстыру әдісі, тең коэффициент әдісі және графикалық шешім әдісі сияқты әдістер ұсынылды. Квадрат теңдеулер факторизация әдісі, түбірді алу әдісі және дискриминант формуласы арқылы қарастырылды. Рационал теңдеулердің айнымалыны ауыстыру, ортақ бөлгішке көбейту секілді маңызды әдістері қарастырылды.

Жұмыстың практикалық бөлігінде теңдеулерді шешудің зерттелген әдістерін қолдану қажет болатын нақты есептер ұсынылды. Есептер тұжырымдалып, теңдеулердің практикалық шешімі жасалды. Бұл маған алған теориялық білімдерімді бекітуге және оларды іс жүзінде қолдануға көмектесті.

---

Зерттеу нәтижесінде теңдеулер математикада маңызды құрал болып табылатыны және біздің өміріміздің әртүрлі салаларында қолданылатыны анықталды. Теңдеулерді шешу әдістерін меңгеру есептерді тиімді шешуге және белгісіз мәндерді табуға мүмкіндік берді.

Қорытындылай келе, теңдеулердің түрлерін және оларды шешу әдістерін зерттеу математикалық білім берудің маңызды кезеңі болып табылады. Ол математикалық ұғымдар туралы түсінігімізді кеңейтеді және олардың аналитикалық ойлауымызды дамытады. Алынған білім мен дағдыларды тек оқуда ғана емес, теңдеулерді шешуді қажет ететін жағдайлар туындайтын күнделікті өмірде де қолданамын деген үміттемін.

ПАЙДАЛАНҒАН ӘДЕБИЕТТЕР ТІЗІМІ

1. 
   Алгебра. Жалпы білім беретін мектептің 8-сыныбына арналған оқулық. Б.Баймұханов, Е.Медеуов, Қ.Базаров. Алматы. Мектеп 2004.
   
2. 
   Алгебра. Жалпы білім беретін мектептің 8-сыныбына арналған оқулық. Б.Баймұханов, Е.Медеуов, Қ.Базаров. Алматы. Жазушы 2007.
   
3. 
   Алгебра 8-класс. Решение задач школьной программы по учебнику
   

Ю.Н. Макарычева. Издание второе, дополненное и исправленное. ЗАО «Славянский дом книги». Москва 2002.

4. Тренажер по математике для подготовки к единому национальному тестированию (ЕНТ). И.П.Рустюмова, С.Т.Рустюмова. Алматы.2011.

5. Алгебра. Жалпы білім беретін мектептің 7-сыныбына арналған оқулық. Ә.Н.Шыныбеков, Д.А.Шыныбеков. Алматы. Атамұра.2017

---

Смотрите также файлы

• В современном строительстве 60% по объему составляет возведение зданий и сооружений из монолитных железобетонных конструкций.docx

• Джордж Беркли.docx

• О допуске лиц, обучающихся по образовательным программам высшего образования, к занятию педагогической деятельностью по общеобразовательным программам.pdf

• Основы оперативного планирования и управления материального потока в производстве..docx

• Практических заданий по дисциплине развитие отраслевых комплексов крупного города.docx