ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 106
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ» |
| Кафедра экономики и управления Форма обучения: заочная/очно-заочная |
ВЫПОЛНЕНИЕ
ПРАКТИЧЕСКИХ ЗАДАНИЙ
ПО ДИСЦИПЛИНЕ
МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ПСИХОЛОГИИ
Группа
Студент
МОСКВА
Практическая работа 1.
Определение числовых характеристик.
Задание 1.
Проведено выборочное обследование частных психологических кабинетов города. Имеются следующие данные о величине посещаемости для 50 кабинетов города (хi - количество клиентов в месяц, млн. руб.; ni - число кабинетов).
| xi | 30-80 | 80-130 | 130-180 | 180-230 | 230-280 | 280-330 |
| ni | 15 | 13 | 7 | 5 | 3 | 2 |
Найти:
а) среднее X, среднеквадратичное отклонение S и коэффициент V;
б) построить гистограмму и полигон частот.
Решение:
Перейдем к простому вариационному ряду, выбирая в качестве значений середины интервалов. Получим:
| xi | 55 | 105 | 155 | 205 | 255 | 305 |
| ni | 15 | 13 | 7 | 5 | 3 | 2 |
Найдем необходимые числовые характеристики на основе последовательных расчетов:
| xi | 55 | 105 | 155 | 205 | 255 | 305 | |
| ni | 15 | 13 | 7 | 5 | 3 | 2 | 45 |
| xi ni | 825 | 1365 | 1085 | 1025 | 765 | 610 | 5675 |
| (xi - Х)2 ni | 75849,48 | 5793,217 | 5842,425 | 31118,16 | 49837,9 | 64003,26 | 232444,4 |
Среднее:
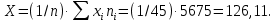
Дисперсия
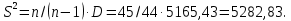
Среднеквадратичное отклонение
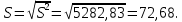
Коэффициент вариации
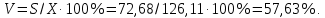
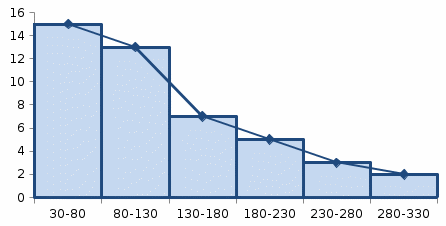
Рис. 1. Гистограмма и полигон частот.
Задание 2.
Из генеральной совокупности извлечена выборка объема n. Найти среднее значение, дисперсию, среднее квадратическое отклонение, исправленную дисперсию, коэффициент вариации, моду и медиану.
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 |
Решение:
Составим таблицу значений.
| xi | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 | |
| ni | 3 | 15 | 30 | 15 | 5 | 4 | 2 | 74 |
| xi ni | 28,5 | 150 | 315 | 165 | 57,5 | 48 | 25 | 789 |
| (xi - Х)2 ni | 4,0368 | 6,534 | 0,768 | 1,734 | 3,528 | 7,1824 | 6,7712 | 30,5544 |
Среднее значение
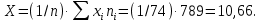
Дисперсия
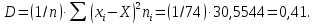
Среднее квадратичное отклонение
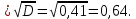
Исправленная дисперсия
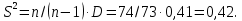
Исправленное среднеквадратичное отклонение
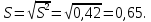
Коэффициент вариации
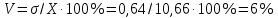
Мода - величина с наибольшей частотой Мо = 10,5
Медиана - величина, находящаяся в середине ряда Ме = 11
Практическая работа 2.
Статистическая обработка данных.
Задание 1.
У 24 девушек - студентов физического и психологического факультетов был измерен уровень вербального интеллекта по методике Векслера. Можно ли утверждать, что одна из групп превосходит другую по уровню вербального интеллекта?
Физики: 123, 134, 126, 131, 134, 132, 126, 132, 127, 127, 136, 133, 136, 135, Психологи: 123, 125, 132, 120, 127, 126, 120, 126, 120, 119,
Решение:
Используем критерий Q Розенбаума. Упорядочим значения в обеих выборках, а затем сформулируем гипотезы:
Н0: Студенты-физики не превосходят студентов-психологов по уровню вербального интеллекта.
Н1: Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта.
| Физики | Психологи |
| 136 | |
| 136 | |
| 135 | |
| 134 | |
| 134 | |
| 133 | |
| 132 | 132 |
| 132 | |
| 131 | |
| 127 | 127 |
| 127 | |
| 126 | 126 |
| 126 | 126 |
| | 125 |
| 123 | 123 |
| S2 | 120 |
| 120 | |
| 120 | |
| 119 |
Определяем количество значений первого ряда, которые больше максимального значения второго ряда: S1 = 6.
Теперь определяем количество значений второго ряда, которые меньше минимального значения первого ряда: S2 = 4.
Вычисляем QЭМП по формуле: QЭМП = S1 + S2 = 6 + 4 = 10.
Определяем критические значения Q для n1 = 14, n2 = 10.
Qкр = 7 при p 0,05;
Qкр = 9 при p 0,01.
Ясно, что чем больше расхождения между выборками, тем больше величина Q.
Н0 отклоняется при QЭМП > Qкр, а при QЭМП < Qкр мы будем
вынуждены принять Н0.
П
 остроим «ось значимости».
остроим «ось значимости».

Q0,05
Q0,01
QЭМП > Qкр

7
9
10
Ответ: Отклоняется Н0. Студенты-физики превосходят студентов-психологов по уровню вербального интеллекта (р 0,01).
Задание 2.
Были протестированы две группы студентов. Тест содержал 60 вопросов. Указано число правильных ответов каждого участника теста.
Можно ли утверждать, что одна из групп превзошла другую группу по результатам теста?
Группа 1: 55,45,42, 40
Группа 2: 46, 41, 38, 35, 34
Решение:
Используем критерий U - критерий Манна-Уитни.
Гипотезы:
Н0: Уровень признака в группе 2 не ниже уровня в группе 1.
Н1: Уровень признака в группе 2 ниже уровня признака в группе 1.
Соблюдены ограничения критерия U:
1. В каждой выборке должно быть не менее 3 наблюдений: n1, n2 3;допускается, чтобы в одной выборке было 2 наблюдения, но тогда во второй их должно быть не менее 5.
2. В каждой выборке должно быть не более 60 наблюдений; n1, n2 60. Однако уже при n1, n2 20 ранжирование становится достаточно трудоемким.
Ранжируем наблюдения:
Меньшему значению начисляется меньший ранг. Наименьшему значению начисляется ранг 1. Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений.
Количество ранжируемых значений = 4 + 5 = 9.
Минимум 34 - ранг 1. Максимум 55 - ранг 9.
Если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы не были равны.
| Группа 1 | Ранг | Группа 2 | Ранг |
| 55 | 9 | | |
| | | 46 | 8 |
| 45 | 7 | | |
| 42 | 6 | | |
| | | 41 | 5 |
| 40 | 4 | | |
| | | 38 | 3 |
| | | 35 | 2 |
| | | 34 | 1 |
| Сумма | 26 | Сумма | 19 |