Файл: 1. основные результаты и направления развития гидроаэромеханики буровых процессов.doc

1. ОСНОВНЫЕ РЕЗУЛЬТАТЫ И НАПРАВЛЕНИЯ РАЗВИТИЯ ГИДРОАЭРОМЕХАНИКИ БУРОВЫХ ПРОЦЕССОВ

Интенсивное изучение форм и законов движения жидкостей в скважинах началось с 1901 г., когда в США на месторождении Спиндлтоп в штате Техас нашел применение механический вращательный способ бурения с промывкой (роторное бурение). В 1911 г., впервые в России, в Сураханском районе были пробурены несколько скважин вращательным способом с промывкой забоя глинистым раствором.

Непрерывное увеличение глубин скважин и сложности горно-геологических условий привели к тому, что процессы промывки и тампонирования скважин стали весьма дорогостоящими и энергоемкими, поэтому возникла необходимость в составлении математической модели циркуляционной системы скважины, позволяющей оптимизировать процессы. Формулирование модели развивалось в двух направлениях: описание основных гидроаэромеханических свойств отдельных элементов и структуры системы в целом.

Исследования основных свойств элементов свелись к нахождению зависимостей между давлением, расходом и временем. Они проходили под влиянием представлений теоретической гидромеханики и практической гидравлики. Укажем наиболее значимые результаты для гидроаэромеханики в бурении.

Основополагающее значение для решения задач буровой гидроаэромеханики имели реологические уравнения, сформулированные:

• в 1685 г. И. Ньютоном для вязких;

• в 1889 г. Ф.Ф. Шведовым и в 1916 г. Е. Бингамом для вязкопластических;

• в 1924 г. В. Оствальдом для псевдопластических сред.

С помощью этих уравнений были получены формулы для распределения давления при установившемся ламинарном течении в круглых трубах:

• вязких (Ж. Пуазейль, 1840—1842 гг.; Г. Стокс, 1846 г.);

• вязкопластических (Е. Букингам, 1921 г.);

• псевдопластических (В. Рабинович, 1929 г., М. Муни, 1931 г.) жидкостей.

Также были найдены решения для течений в концентричных кольцевых каналах:

• вязких (Т. Буссинеск, 1891 г.);

• вязкопластических (М.П. Воларович и А. М. Гуткин, 1946 г.);

• псевдопластических (А. Фредриксон и Р. Берд, 1958 г.) жидкостей.

Опираясь на формулы Букингама и Воларовича—Гуткина для течения вязкопластических жидкостей в круглых трубах и концентричных кольцевых каналах, К. Гродде в 1960 г. применил удобный графический метод расчета перепада давления.

В 1931 г. В.Н. Щелкачев рассмотрел ламинарное установившееся течение вязкой жидкости в эксцентричном кольцевом канале и получил формулу для распределения давления. Р. Мак-Лин, Ц. Менри и В. Уайтекер в 1967 г. дали общую схему приближенного расчета распределения давления при ламинарном течении реологически стационарных жидкостей в эксцентричном кольцевом канале.

---

Устойчивость ламинарного движения вязких жидкостей в круглых трубах экспериментально исследована О. Рейнольдсом в период 1876—1883 гг. Им установлен критерий перехода ламинарного течения в турбулентное. Потерю устойчивости ламинарного движения вязкопластических жидкостей Б. Хедстрем в 1951 г. охарактеризовал числами Рейнольдса и Сен-Венана.

На основании теории пограничного слоя, разработанной Л. Прандтлем в 1904— 1925 гг. для турбулентного движения вязкой жидкости в трубах с гладкими и шероховатыми стенками, А.Д. Альтшуль в 1970 г. получил зависимость для коэффициентов гидравлических сопротивлений.

Создавая теорию многоступенчатых турбин, П.П. Шумилов в 1933—1941 гг. дал формулу для определения перепада давления в турбобурах. Для расчета изменения давления в местных сопротивлениях циркуляционной системы X. Геррик в 1932 г. использовал метод эквивалентных длин. П.П. Шумилов в 1940 г. для определения перепада давления в замках применил формулу Борда— Карно, а в долотных отверстиях — формулу Торичелли. В 1851 г. Г. Стокс рассмотрел ламинарное обтекание шара вязкой жидкостью. Экспериментальные исследования сопротивления при обтекании твердых сферических частиц в широком диапазоне чисел Рейнольдса обобщены в виде кривой Релея. В 1932 г. Р.И. Шищенко и Б.Д. Бакланов исследовали условия равновесия и обтекания частиц глинистым раствором.

С.М. Тарг в 1946 г. нашел распределение давлений при ламинарном установившемся движении вязкой жидкости в осесимметричном кольцевом канале, одна из стенок которого перемещается с постоянной скоростью. В 1954 г. Н.А. Гукасов рассмотрел ламинарное течение вязкопластической жидкости в концентрическом кольцевом канале с подвижной внутренней стенкой.

Основные уравнения гидродинамики многофазных жидкостей, замкнутые с помощью эмпирических зависимостей для концентрации и коэффициента гидравлических сопротивлений, вывел С.Г. Телетов в 1945 г. На их базе получены распределения давлений в трубах и кольцевых каналах при промывке скважины аэрированной жидкостью или продувке ее газом.

Фундаментальный вклад в решение проблемы неустановившегося движения в гидравлических системах с учетом сжимаемости жидкости и упругости стенок внес Н.Е. Жуковский в 1898—1921 гг. На основе его трудов главным образом советскими учеными разработана теория одноразмерного неустановившегося движения вязкой жидкости. Она позволяет методом характеристик решать многие задачи.

В связи с задачами разработки нефтяных и газовых месторождений в первую очередь в трудах Н.Н. Павловского (1922 г.), Л.С. Лейбензона (1934 г.), В.Н. Щелкачева, И.А. Чарного, М. Маскета и многих других подробно изучено движение пластовых флюидов в пористой среде, необходимое для решения задач вскрытия продуктивных отложений и борьбы с осложнениями при бурении.

---

Наряду с изучением гидроаэромеханических характеристик элементов системы развиваются исследования системы пласт—скважина в целом. В них устанавливаются взаимосвязи между элементами системы, необходимые для совместного решения всех уравнений, характеризующих отдельные элементы. Например, с целью определения подачи и давления буровых насосов для циркуляции промывочной жидкости такую задачу рассмотрели в 1932 г. И.Л. Векслер и X. Геррик. В 1938 г. Н.И. Шацов разработал схему методики выбора числа и параметров цементировочных агрегатов для одноступенчатого тампонирования скважин.

В последние десятилетия А.Х. Мирзаджанзаде и его ученики развивают анализ гидроаэромеханических процессов с помощью стохастических и адаптационно-обучающихся моделей.

Изучением местных и линейных гидравлических потерь давления занимались Б.И. Мительман, В.И. Липатов, Б.И. Есьман и др. Вопросы возникновения турбулентности исследовались Э.К. Латыповым, Б.С. Филатовым, В.И. Липатовьм, Г.Г. Габузовым и др.

Детальное изучение температурного режима бурящихся скважин началось в 1965 г. В разработке методик прогнозирования и регулирования температурного режима скважин и горных выработок участвовали Ленинградский горный институт (Б.Б. Кудряшов, Ю.Д. Дядькин), ВНИИКрнефть (А.И. Булатов, Ю.М. Проселков, И.А. Карманов), ГрозНИИ (Г.Г. Поляков) и др.

В настоящее время намечается тенденция развития системного подхода к гидроаэромеханике бурения, прежде всего в направлении построения структур моделей системы скважина—пласт в целом как упрощенных, так и более сложных, требующих применения разнообразных методов математического аппарата и использования компьютерной техники.
2. РЕОЛОГИЯ БУРОВЫХ И ТАМПОНАЖНЫХ РАСТВОРОВ

2.1. СВЕДЕНИЯ О РЕОЛОГИИ. ОСНОВНЫЕ УРАВНЕНИЯ

В широком смысле реология представляет раздел физики, изучающий деформацию тел, включая их текучесть. Согласно этому определению, она охватывает и сферы других, самостоятельных, наук: гидро- и аэродинамику, теорию упругости, теорию пластичности и даже металлургию.

Практически же реология изучает лишь те материалы, которые по своему поведению занимают промежуточное положение между твердыми и жидкими телами; следовательно, реология — это раздел механики деформируемых тел, находящийся на стыке между теориями пластичности и упругости, с одной стороны, и механикой жидкости — с другой.

---

Реология появилась ввиду необходимости описать поведение некоторых веществ с очень сложными свойствами, для которых существующие теории представлялись недостаточными. К таким веществам относятся суспензии, эмульсии, полимеры, пищевые продукты, бетон, керамические материалы, асфальт, некоторые горные породы и многие другие материалы.

В более узком смысле цель реологии как науки сводится к изучению реологических уравнений в самой обобщенной их форме, описывающих поведение различных материалов.

Реологическое уравнение для какого-либо материала выражает зависимость между напряжением и соответствующей деформацией, т. е. между кинематикой и динамикой движения частиц вещества. Релаксация—уменьшение во времени напряжений при постоянных деформациях и ползучесть—увеличение деформаций во времени при постоянных напряжениях относятся к двум типичным процессам, изучаемым реологией.

Точнее, реологическое уравнение представляет соотношение между напряжениями , вызванными деформациями , и их производными во времени:

(1)

Скалярные параметры, фигурирующие в этом уравнении и характеризующие реологические свойства материала, называются реологическими константами (модулями, параметрами, коэффициентами), а напряжения, деформации и их производные составляют реологические переменные. В общем случае реологические параметры зависят как от некоторых нереологических величин (например, характеристик температурного или электромагнитного поля), так и от некоторых инвариантов напряжения (или деформации), что придает реологическому уравнению нелинейный характер.

Следует отметить, что имеют место деформации и не сопровождаемые напряжениями, а возникающие вследствие изменений температуры, влажности, каких-либо физико-химических реакций, т.е. факторов, которые необходимо принимать во внимание. В реологии выделяют три основных раздела:

• феноменологическая реология количественно и качественно исследует и изучает деформации и текучесть тел без анализа их причин;

• макрореология рассматривает тела (гомогенные или квазигомогенные, изотропные или квазиизотропные) как непрерывные среды — гомогенные и изотропные, абстрагируясь при этом от их внутренней структуры;

• микрореология выявляет свойства и реологическое поведение вещества путем исследования его состава, кристаллической структуры, формы и длины макромолекул, свойств его компонентов и т.д. Например, вязкость суспензий слабой концентрации можно рассчитать при помощи формулы, выведенной Эйнштейном в 1905 г.

---

2.2. РЕОЛОГИЧЕСКИЕ МОДЕЛИ

Реологические уравнения являются математическими моделями, отражающими идеальное поведение реальных тел.

2.2.1. Фундаментальные модели

Все природные тела в той или иной степени обладают тремя основными свойствами: упругостью, вязкостью и пластичностью. Этот факт и привел к созданию трех базовых моделей. С достаточно высокой точностью они описывают поведение многих категорий природных материалов.

Модель идеально упругой среды характеризует поведение твердого тела, в котором деформация исчезает одновременно с напряжением. Механическая работа, совершаемая под действием внешних нагрузок, ведет к накоплению потенциальной энергии, которая при устранении этих нагрузок возвращает телу исходную форму и размеры. Теоретически деформация является мгновенной, т. е. независимой от времени. При незначительных деформациях зависимость между напряжением и деформацией является линейной функцией (рис. 2.1 а), которая для простого (одноосного) сдвига описывается законом Гука

 =G (2.2)

где  - угловая деформация; G - поперечный модуль упругости (реологическая постоянная тела).

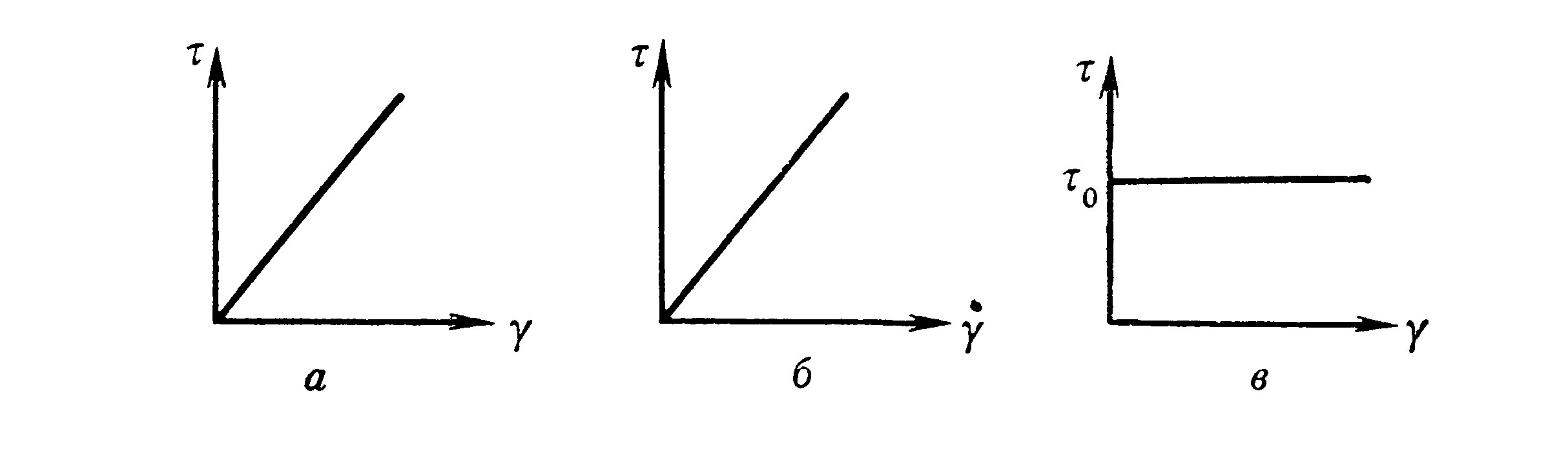Рисунок 2.1. Кривые течения для фундаментальных моделей

а – идеально упругая среда, б – идеально вязкая среда, в – жестко-пластичная среда
Модель идеально вязкой среды отражает линейное отношение между возникающими в жидкости напряжениями и скоростью деформации (рис. 2.1б). При простом сдвиге это соотношение называется законом Ньютона:

 = (2.3)

где — реологическая постоянная модели, или вязкость; — скорость деформации, вызванная касательным напряжением .

Уравнение (2.3), в основном, определяет текучесть газов, воды и некоторых однофазных сред с низкой молекулярной массой.

---