,.(2.3)
где - вероятность безотказной работы элемента 10;

-вероятность безотказной работы элемента А;

-вероятность безотказной работы элемента В;

- вероятность безотказной работы элемента 8.

Для повышения вероятности безотказной работы системы можно использовать два метода:

а) повышения надежности элементов;

б) структурного резервирования элементов системы.

---

2.2 Преобразование заданной структурной схемы и определение показателей надёжности

Структурная схема надежности приведена на рисунке. Значения интенсивности отказов элементов даны в 1/ч:
λ₁ = λ₁₃ = λ₁₄ =λ₁₅ =0,01

λ₂ = λ₃ = λ₈ = λ₉ =0,2

λ₄ =0,1

λ₅ = λ₆ =0,3

λ₇ =0,5

λ₁₀ = λ₁₁ = λ₁₂ =1

γ = 75 %


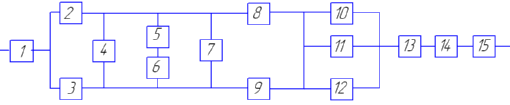
Рисунок 4 - Исходная схема системы
Так как по условию все элементы системы работают в периоде нормальной эксплуатации, то вероятность безотказной работы элементов с «1» по «15» (рисунок ) подчиняются экспоненциальному закону:
(2.4)
где р_i - вероятность безотказной работы ί - го элемента;

λ_ί - интенсивность отказов ί - го элемента;

t - время наработки.

В исходной схеме элементы «5» и «6» образуют последовательное соединение, которое заменяем квазиэлементом «А». Так как р_{5 =} р₆ , то для определения вероятности безотказной работы элемента «А» получим:

(2.5)

где р_А - вероятность безотказной работы элемента «А»;

р₅ - вероятность безотказной работы элемента «5».

Р₆ - вероятность безотказной работы элемента «6».

Элементы «10», «11» и «12»образуют параллельное соединение. Заменяем их квазиэлементом «B». Так как р_{10 =} р₁₁₌ р_12, то для определения вероятности безотказной работы элемента «В» получим:
(2.6)
где р_B - вероятность безотказной работы элемента «B»;

Q_B - вероятность отказа элемента «B»;

q₁₀ - вероятность отказа элемента «10»;

q₁₁ - вероятность отказа элемента «11»;

---

q₁₂ - вероятность отказа элемента «12»;

р₁₀ - вероятность безотказной работы элемента «10».

Элементы «13», «14» и «15» образуют последовательное соединение. Заменяем их квазиэлементом «С». Так как р_{13 =} р₁₄₌ р_15, то для определения вероятности безотказной работы элемента «С» получим:
(2.7)
где р_С - вероятность безотказной работы элемента «С»;

р₁₃ - вероятность безотказной работы элемента «13»;

р₁₄ - вероятность безотказной работы элемента «14»;

р₁₅ - вероятность безотказной работы элемента «15».

Элементы «4», «7» и квазиэлемент «А» образуют параллельное соединение. Заменяем их квазиэлементом «D».




. (2.8)
где р_D - вероятность безотказной работы элемента «D»;

Q_D - вероятность отказа элемента «D»;

q₄ - вероятность отказа элемента «4»;

q_А - вероятность отказа элемента «А»;

q₇ - вероятность отказа элемента «7»;

р₄ - вероятность безотказной работы элемента «4»;

р_А - вероятность безотказной работы квазиэлемента «А»;

р₇ - вероятность безотказной работы элемента «7»;

После преобразований промежуточная схема изображена на рисунке 5


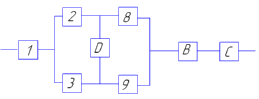
Рисунок 5 - Промежуточная схема
Элементы «2», «3», «8», «9» и квазиэлемент «D» образуют мостиковую систему, которую можно заменить квазиэлементом «Е».

Для расчёта вероятности безотказной работы воспользуемся матодом разложения относительно особого элемента. В качестве особого элемента выберем квазиэлемент «D», тогда
(2.9)
где - вероятность безотказной работы мостиковой схемы при абсолютно надежном элементе «D» (рис а);

- вероятность безотказной работы мостиковой схемы при отказавшем элементе «D» (рис. б).

---

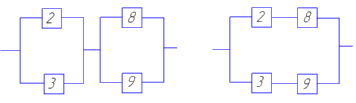
(а) (б)

Рисунок 6 - Преобразование мостиковой схемы
; (2.10)

; (2.11)

.(2.12)
После преобразованья схема изображена на рисунке 7


Рисунок 7 - Преобразованная схема
В преобразованной схеме (рисунок 7 ) элементы «p1», «Е» «B» и «С» образуют последовательное соединение. Тогда вероятность безотказной работы всей системы:
(2.13)
Рассчитаем вероятности элементов и вероятность безотказной работы всей системы по формулам (2.1)-(2.10).
При наработке t = 0,4·10⁶ ч.:

При наработке t = 0,6·10⁶ ч.:


При наработке t = 0,8·10⁶ ч.:

При наработке t = 1·10⁶ ч.:

При наработке t = 1,5·10⁶ ч.:

При наработке t = 2·10⁶ ч.:


При наработке t = 2,5·10 ч.:


Результаты расчетов вероятностей безотказной работы элементов с «1» по «15» исходной схемы по формуле (2.1) для наработки до 2,5

---

10⁶ часов представлены в таблице 1.

Результаты расчетов вероятностей безотказной работы квазиэлементов «A», «B», «C», «D», «Е» и всей системы также представлены в таблице 1.

На рисунке представлен график зависимости вероятности безотказной работы системы «P» от времени (наработки) t.

По графику (рисунок, кривая P) находим для ( ) - процентную наработку системы ч.

Проверочный расчет при ч показывает (таблица 1), что .

По условиям задания повышенная - процентная наработка системы ч.

Расчет показывает (таблица 1), что при ч для элементов преобразованной схемы, изображенной на рисунке p₁=0,987416, p_Е=0,900587, p_B=0,629616 ,p_C=0,962721, P=0,53902. Следовательно, из последовательно соединенных элементов минимальное значение вероятности безотказной работы имеет квазиэлемент «В», и именно увеличение его надежности даст максимальное увеличение надежности системы в целом.

Для того чтобы при ч система в целом имела вероятность безотказной работы, необходимо, чтобы квазиэлемент «В» имел вероятность безотказной работы (см. формулу (2.13))
(2.14)
где

---

Смотрите также файлы

• О двух маленьких породах собак.doc

• Профессиональное образовательное учреждение Челябинский юридический колледж.doc

• Отчет по практике Колледж мэси отчет по производственной.pdf

• Практических заданий по дисциплине основы математического моделирования социальноэкономических процессов.docx

• Выполнение практических заданий по дисциплине история экономики.doc