Файл: Курсовой проект 36 с., 9 рис., 1 табл., 5 источников.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 25.10.2023
Просмотров: 77
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
- вероятность безотказной работы элемента «В»;
- вероятность безотказной работы системы, 
0,75.
Очевидно, значение
, полученное по формуле (2.14), является минимальным для выполнения условия увеличения наработки не менее, чем в полтора раза, при более высоких значениях увеличение надежности системы будет большим.
Для определения минимально необходимой вероятности безотказной работы элементов c 10 по 12 (рисунок ) необходимо решить уравнение относительно
при
.
Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (2.), то для элементов с «10» по «12» при 
ч находим:
где
- интенсивность отказов элементов «10», «11», «12».
Рассчитаем вероятности безотказной работы данных элементов, квазиэлемента «В′» и всей системы «P′» при разной наработке.
При наработке t = 0,4·106 ч.:
При наработке t = 0,6·106 ч.:
При наработке t = 0,8·106 ч.:
При наработке t = 1·106 ч.:
При наработке t = 1,5·106 ч.:
При наработке t = 2·106 ч.:
При наработке t=2,5·106
Таким образом, для увеличения
- процентной наработки системы необходимо увеличить надежность элементов «10», «11», «12» и снизить интенсивность их отказов с 1 до 0,4·10-6 ч
, т.е. в 2,5 раза. Результаты расчетов для системы с увеличенной надежностью элементов «10», «11», «12» приведены в таблице 1. Там же приведены расчетные значения вероятности безотказной работы квазиэлемента «В`» и системы в целом «P`». При t=1,275·106 ч вероятность безотказной работы системы 
, что соответствует условиям задания. График приведен на рисунке.
Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям (см. выше) также выбираем квазиэлемент «В», вероятность безотказной работы которого после резервирования должна быть не ниже 
(см. формулу (2.14)).
Для элемента «В» - резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция
дискретна.
Для повышения надежности системы «В» добавляем к ней элементы, идентичные по надежности исходным элементам «10», «11», «12», до тех пор, пока вероятность безотказной работы квазиэлемента «В» не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом:
- добавляем элемент «16», получаем систему из 4 параллельно соединенных элементов:
добавляем элементы «17,18» получаем систему из 6 параллельно соединенных элементов:
добавляем элемент «19» получаем систему из 7 параллельно соединенных элементов:
Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рисунок 1) систему 3 параллельных элементов достроить элементами «16-19» до системы из 7 параллельных элементов (рисунок).
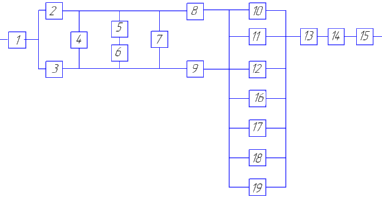
Рисунок 8 - Структурная схема системы после структурного резервирования
Тогда, вероятность безотказной работы квазиэлемента «В′′» и вероятность безотказной работы всей системы:
При наработке t = 0,4·106 ч. равна:
При наработке t = 0,6·106 ч.:
При наработке t = 0,8·106 ч.:
При наработке t = 1·106 ч.:
При наработке t = 1,5·106 ч.:
При наработке t =2·106 ч.:
При наработке t =2,5·106 ч.:
Результаты расчетов вероятностей безотказной работы квазиэлемента «В``» и системы в целом «P``» представлены в таблице 1.
Расчеты показывают, что при
ч.
, что соответствует условию задания.
Таблица 1
Расчет вероятности безотказной работы системы
На рисунке 9 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов с «10» по «12» (кривая
) и после структурного резервирования (кривая 
).
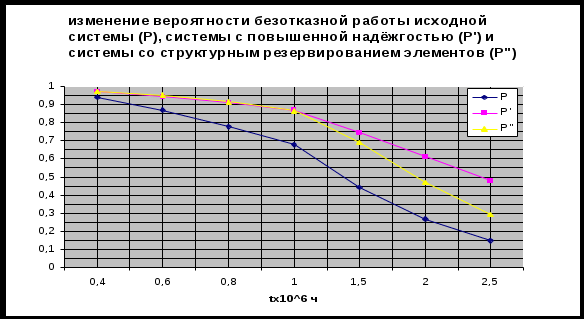
Рисунок 9 - Изменение вероятности безотказной работы систем
Выводы:
а) на рисунке представлена зависимость вероятности безотказной работы системы (кривая
). Из графика видно, что 75% - наработка исходной системы составляет 
часов;
б) для повышения надежности и увеличения 75% - наработки системы в полтора раза (до
часов) предложены два способа:
повышение надежности элементов «10», «11», «12» и уменьшение их отказов;
нагруженное резервирование основных элементов «10», «11», «12» идентичными по надежности резервными элементами c «16» по «19» (рисунок 8).
в) анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис.9 ) показывает, что первый способ повышения надежности системы (уменьшение интенсивности отказов элементов) предпочтительнее второго, так как в период наработки до 1,275
106 часов вероятность безотказной работы системы (кривая 
) выше, чем при структурном резервировании (кривая 
).
При выполнении данной курсовой работы были выполнены два задания. Первое задание связано с построением структурной схемы надежности установки подготовки нефти и расчетом надежности данной системы.
- вероятность безотказной работы системы, 0,75.Очевидно, значение
, полученное по формуле (2.14), является минимальным для выполнения условия увеличения наработки не менее, чем в полтора раза, при более высоких значениях увеличение надежности системы будет большим.Для определения минимально необходимой вероятности безотказной работы элементов c 10 по 12 (рисунок ) необходимо решить уравнение относительно
при . Так как по условиям задания все элементы работают в периоде нормальной эксплуатации и подчиняются экспоненциальному закону (2.), то для элементов с «10» по «12» при ч находим: где
- интенсивность отказов элементов «10», «11», «12».Рассчитаем вероятности безотказной работы данных элементов, квазиэлемента «В′» и всей системы «P′» при разной наработке.
При наработке t = 0,4·106 ч.:
При наработке t = 0,6·106 ч.:
При наработке t = 0,8·106 ч.:
При наработке t = 1·106 ч.:
При наработке t = 1,5·106 ч.:
При наработке t = 2·106 ч.:
При наработке t=2,5·106
Таким образом, для увеличения
- процентной наработки системы необходимо увеличить надежность элементов «10», «11», «12» и снизить интенсивность их отказов с 1 до 0,4·10-6 ч , т.е. в 2,5 раза. Результаты расчетов для системы с увеличенной надежностью элементов «10», «11», «12» приведены в таблице 1. Там же приведены расчетные значения вероятности безотказной работы квазиэлемента «В`» и системы в целом «P`». При t=1,275·106 ч вероятность безотказной работы системы , что соответствует условиям задания. График приведен на рисунке. Для второго способа увеличения вероятности безотказной работы системы - структурного резервирования - по тем же соображениям (см. выше) также выбираем квазиэлемент «В», вероятность безотказной работы которого после резервирования должна быть не ниже (см. формулу (2.14)).Для элемента «В» - резервирование означает увеличение общего числа элементов. Аналитически определить минимально необходимое количество элементов невозможно, т.к. число элементов должно быть целым и функция
дискретна.Для повышения надежности системы «В» добавляем к ней элементы, идентичные по надежности исходным элементам «10», «11», «12», до тех пор, пока вероятность безотказной работы квазиэлемента «В» не достигнет заданного значения.
Для расчета воспользуемся комбинаторным методом:
- добавляем элемент «16», получаем систему из 4 параллельно соединенных элементов:
добавляем элементы «17,18» получаем систему из 6 параллельно соединенных элементов:
добавляем элемент «19» получаем систему из 7 параллельно соединенных элементов:
Таким образом, для повышения надежности до требуемого уровня необходимо в исходной схеме (рисунок 1) систему 3 параллельных элементов достроить элементами «16-19» до системы из 7 параллельных элементов (рисунок). Рисунок 8 - Структурная схема системы после структурного резервирования
Тогда, вероятность безотказной работы квазиэлемента «В′′» и вероятность безотказной работы всей системы:
При наработке t = 0,4·106 ч. равна:
При наработке t = 0,6·106 ч.:
При наработке t = 0,8·106 ч.:
При наработке t = 1·106 ч.:
При наработке t = 1,5·106 ч.:
При наработке t =2·106 ч.:
При наработке t =2,5·106 ч.:
Результаты расчетов вероятностей безотказной работы квазиэлемента «В``» и системы в целом «P``» представлены в таблице 1.
Расчеты показывают, что при
ч.
, что соответствует условию задания. Таблица 1Расчет вероятности безотказной работы системы
| Элемент | λx10-6 ч-1 | Наработка t*106 ч | ||||||
| | | 0.4 | 0,6 | 0,8 | 1 | 1.5 | 2 | 2.5 |
| 1,13,14,15 | 0.01 | 0.996035 | 0.994058 | 0.992085 | 0.990117 | 0.985212 | 0.980331 | 0.975474 |
| 2,3,8,9 | 0.2 | 0.923615 | 0.887639 | 0.853064 | 0.819836 | 0.742321 | 0.672132 | 0.608581 |
| 4 | 0.1 | 0.961049 | 0.942146 | 0.923613 | 0.905448 | 0.861581 | 0.819836 | 0.780116 |
| 5,6 | 0.3 | 0.887639 | 0.836285 | 0.787903 | 0.742321 | 0.639567 | 0.551038 | 0.474763 |
| 7 | 0.5 | 0.819836 | 0.74232 | 0.672132 | 0.608581 | 0.474763 | 0.370372 | 0.288932 |
| 10,11,12 | 1 | 0.672132 | 0.551038 | 0.451761 | 0.370372 | 0.225404 | 0.137174 | 0.083482 |
| A | - | 0.787903 | 0.699373 | 0.620791 | 0.551312 | 0.409046 | 0.303624 | 0.225391 |
| В | - | 0.964755 | 0.909504 | 0.835218 | 0.750460 | 0.535345 | 0.367702 | 0.231024 |
| C | - | 0.988152 | 0.982284 | 0.976442 | 0.970643 | 0.956289 | 0.942146 | 0.928212 |
| D | - | 0.998513 | 0.995522 | 0.990501 | 0.983381 | 0.957042 | 0.921014 | 0.878893 |
| E | - | 0.988351 | 0.974823 | 0.956987 | 0.935412 | 0.868467 | 0.788889 | 0.703311 |
| P | - | 0.938482 | 0.865717 | 0.774286 | 0.677430 | 0.438339 | 0.266096 | 0.147116 |
| 10’,11’,12’ | 0,4 | 0.853064 | 0.787903 | 0.727719 | 0.672132 | 0.551038 | 0.451761 | 0.370370 |
| B’ | - | 0.996828 | 0.990459 | 0.979814 | 0.964755 | 0.909504 | 0.835218 | 0.750393 |
| P’ | - | 0.969682 | 0.942775 | 0.908333 | 0.867292 | 0.744178 | 0.608565 | 0.477858 |
| B" | - | 0.999593 | 0.996323 | 0.985114 | 0.960772 | 0.832682 | 0.643992 | 0.456766 |
| P" | - | 0.972172 | 0.948354 | 0.913246 | 0.863711 | 0.681279 | 0.469234 | 0.290873 |
На рисунке 9 нанесены кривые зависимостей вероятности безотказной работы системы после повышения надежности элементов с «10» по «12» (кривая
) и после структурного резервирования (кривая ). Рисунок 9 - Изменение вероятности безотказной работы систем
Выводы:
а) на рисунке представлена зависимость вероятности безотказной работы системы (кривая
). Из графика видно, что 75% - наработка исходной системы составляет часов;б) для повышения надежности и увеличения 75% - наработки системы в полтора раза (до
часов) предложены два способа:повышение надежности элементов «10», «11», «12» и уменьшение их отказов;
нагруженное резервирование основных элементов «10», «11», «12» идентичными по надежности резервными элементами c «16» по «19» (рисунок 8).
в) анализ зависимостей вероятности безотказной работы системы от времени (наработки) (рис.9 ) показывает, что первый способ повышения надежности системы (уменьшение интенсивности отказов элементов) предпочтительнее второго, так как в период наработки до 1,275
106 часов вероятность безотказной работы системы (кривая ) выше, чем при структурном резервировании (кривая ). 
ЗАКЛЮЧЕНИЕ
При выполнении данной курсовой работы были выполнены два задания. Первое задание связано с построением структурной схемы надежности установки подготовки нефти и расчетом надежности данной системы.