ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая организация высшего образования
«МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»
Кафедра экономики и управления Форма обучения: заочная
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙПО ДИСЦИПЛИНЕТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКАГруппа СмМ20Э211СтудентВ.А. КолпаковаМОСКВА 2021Задание 1.Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет.1.1. Чему равна вероятность того, что, вынимая четыре буквы, получим слово РЕКА?Решение:Найдем вероятность выбора первой буквы Р:Количество событий = общему количеству букв = 6.Из них благоприятных событий (подходящих букв) = 1.Вероятность по формуле Лапласа: Р = 1 / 6.Вероятность, что вторая буква Е: Р = 1/5 (из остав. 5ти букв 1 Е);Вероятность того, что третья буква будет К: Р = 1/4 (из остав. 4х букв 1 К);Вероятность того, что четвертая буква будет А: Р = 2/3(из остав. 3х букв 2 А);Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А: Р = (1 / 6) * (1 / 5) * (1 / 4) * (2 / 3) = 1/180=0,005Ответ: Вероятность того, что, вынимая четыре буквы, получим слово РЕКА равна 0,005.1.2. Какова вероятность сложить слово КАРЕТА при вынимании всех букв?Решение:Найдем вероятность выбора первой буквы К:Количество событий = общему количеству букв = 6.Из них благоприятных событий (подходящих букв) = 1.Вероятность по формуле Лапласа: К = 1 / 6.Вероятность, что вторая буква А: Р = 2/5 (из остав. 5ти букв 2 А);Вероятность того, что третья буква будет Р: Р = 1/4 (из остав. 4х букв 1 Р);Вероятность того, что четвертая буква будет Е: Р = 1/3(из остав. 3х букв 1 Е);
Вероятность того, что пятая буква будет Т: Р = 1/2 (из остав. 2х букв 1 Т);Вероятность того, что шестая буква будет А: Р = 1/1(из остав. 1х букв 1 А);Вероятность взаимосвязанных событий, что поочередно вынуты буквы К, А, Р, Е, Т, А: Р = (1 / 6) * (2 / 5) * (1 / 4) * (1 / 3) * (1/2) * (1/1) = 1/360=0,003Ответ: Вероятность того, что, при вынимании всех букв буквы, получим слово КАРЕТА равна 0,003.Задание 2.Дискретная случайная величина ξ задана следующим законом распределения:
????
4
6
10
12
p
0,4
0,1
0,2
0,3
Найти математическое ожидание, дисперсию и среднее квадратическое отклонение.Решение:Математическое ожидание находим по формуле m = ∑ξipi.Математическое ожидание M[ξ].M[ξ] = 4*0,4+6*0,1+10*0,2+12*0,3=7,8Дисперсию находим по формуле d = ∑ξ2ipi - M[ξ]2.Дисперсия D[ξ].D[ξ] = 42*0,4 + 62*0,1 + 102*0,2 + 122*0,3 – = 73,2 – 60,84 = 12,4Среднее квадратическое отклонение σ(ξ).Ответ: M[ξ] = 7.8; D[ξ]=12.4; σ [ξ]=3.516Задание 3.Возможные значения дискретной случайной величины равны: -2, 1, 4. При условии, что заданы математическое ожидание M[ξ] = 1.9, а также M[ξ]2= 7.3, найти вероятности , , которые соответствуют дискретным значениям случайной величины.Решение:Поскольку , а и , то получим систему из трех уравнений:
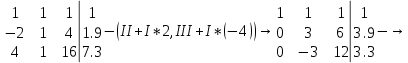
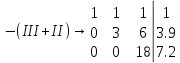
Решим ее методом Гаусса:Ранг матрицы системы равен рангу расширенной матрицы, значит, система совместна. Тогда получим: тогда тогда тогда Ответ:
