_{Методические указания к выполнению контрольной (экзаменационной) работы по дисциплине «Математика. Часть 3»1. Общие указания.}Перед решением контрольной работы следует полностью выписать её условие. Решения задач располагайте в порядке возрастания номеров, указанных в задании.Решения следует излагать, объясняя и мотивируя основные действия по ходу решения. Необходимые рисунки следует помещать в тексте по ходу решения. Ответы в конце решения задачи следует выделять. Желательно использование текстового редактора и редактора формул. В крайнем случае, принимаются сканы отчетливо выполненных рукописных текстов и рисунков.Контрольную, а также и экзаменационную работу, следует посылать отдельным файлом, помещая в начале титульный лист и задание.При необходимости можно использовать справочник по элементарной и высшей математике, прилагаемый к курсу.Работа может быть зачтена даже в случае незначительных ошибок в решении, но может быть возвращена на доработку в случае существенной ошибки.2. Примеры решения задач.Задание 1. 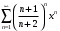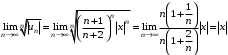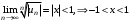Найти область сходимости степенного рядаРешение:Применим к ряду из модулей радикальный признак Коши:Потребуем, чтобы:Проверяем сходимость ряда на концах полученного интервала. Для этого подставляем в исходный ряд вместо значения концов интервала и получаем числовые ряды, сходимость которых поверяем с помощью признаков сходимости числовых рядов.При 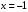, получим ряд: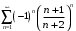Полученный ряд является знакочередующимся, и расходится по признаку Лейбница, т.к.:

---

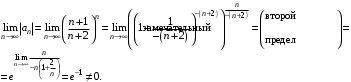
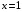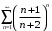
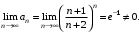
При , получим ряд:Полученный ряд является знакоположительным, и расходится т.к. не выполнен необходимый признак сходимости:Таким образом, на концах промежутка ряд расходится, и в интервал сходимости мы их не включаем.Ответ: Интервал сходимости ряда 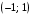.Задание 2. Разложить функцию в ряд Фурье на данном отрезке
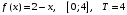
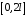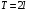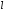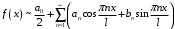
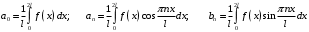
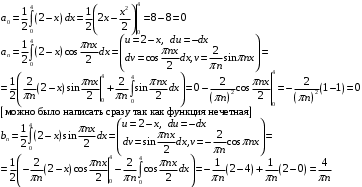
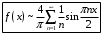
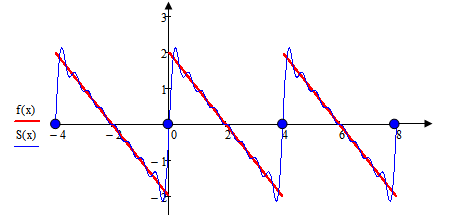
(период Т)_{Решение:}Тригонометрический ряд Фурье на периоде . Период , полупериод .Коэффициенты ищем по формулам:_{Для заданной функции:}Ряд Фурье: График суммы ряда 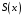в точках непрерывности функции совпадает с графиком 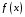, а в точках разрыва первого рода. 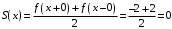(по теореме Дирихле).Ответ: 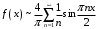.Задание 3. Начертить область на комплексной плоскости по данным условиям: 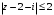, , 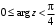, 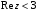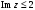.Решение:Модуль комплексного числа :

---

.


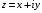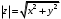
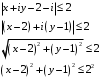
Область внутри круга радиуса 2, с центром в точке (2;1), граница принадлежит области.

Аргумент комплексного числа называется угол между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке: .



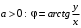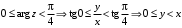
_Прямая 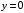– действительная ось принадлежит области.

Действительная часть: 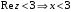полуплоскость правее прямой 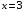, граница области не принадлежит.

Мнимая часть: 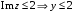полуплоскость ниже прямой 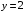, граница области принадлежит.

Начертим область:


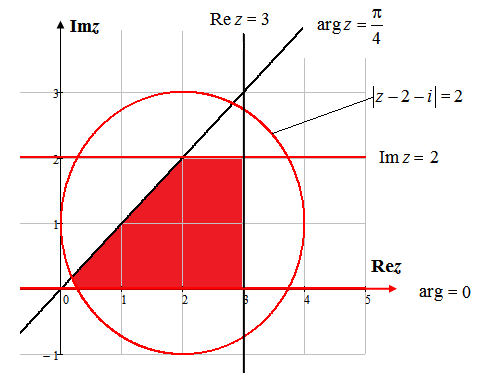
Черные границы области не принадлежат.
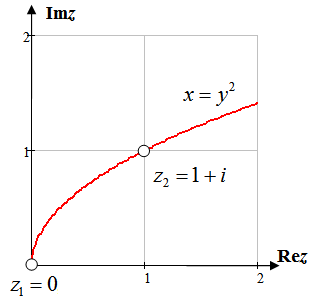
Задание 4. Вычислить интеграл по дуге 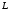от точки 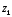до точки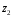

, : , ,
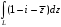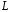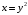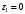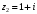
Решение:

Имеем:



.

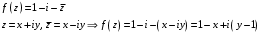
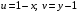Согласно:

,

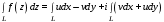получим:







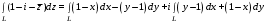
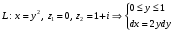
Искомый интеграл:


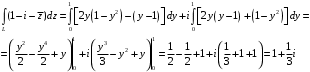
Ответ: .
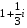Задание 5. Вычислить интеграл по замкнутому контуру с помощью вычетов

---

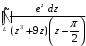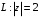
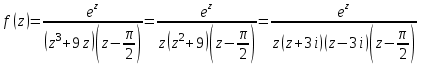
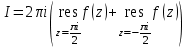
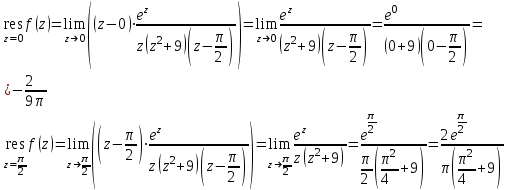
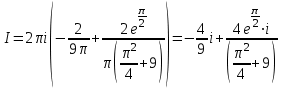
; Решение:Функция:имеет в круге |z|<2 две особые точки: z­₁=0, z₂=/2, являющиеся простыми полюсами. Следовательно, по основной теореме о вычетах:вычисляя вычеты f(z) в указанных точках, имеем:Следовательно, Ответ: 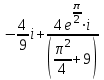2>

---

Смотрите также файлы

• Тема Планирование как инструмент управления проектом. Сущность бизнеспланирования Задание 1.docx

• Методики, авторы, на какие психические процессы направлена.rtf

• Учебное пособие для вузов Б. Ф. Азаров, ив. Карелина, он. Романенко, ли. Хлебородова под ред. Б. Ф. Азарова е изд, перераб и доп.pdf

• Аристотель Стагирит ( 384 322 гг до н э. ).rtf

• .docx