Добавлен: 26.10.2023
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра автоматизированных систем управления (АСУ)
Отчет
По дисциплине «Математика»
Контрольная работа №1
Вариант 5
| | Выполнил: Студент гр. _______________ / «____»_______________2023г. |
| | Проверил: ______________ / «____»_______________2023г. |
Томск 2023
Содержание
1. Введение……………………………………………………...…………………4
2. Найти неопределённые интегралы ……………………………………………5
2.1. Пример №1…………………………………………………………….…….5
2.2. Пример №2…………………………………………………………….…….5
2.3. Пример №3…………………………………………………………….…….5
2.4. Пример №4…………………………………………………………….…….5
2.5. Пример №5…………………………………………………………….…….5
2.6. Пример №6…………………………………………………………….…….6
2.7. Пример №7…………………………………………………………….…….7
2.8. Пример №8…………………………………………………………….…….7
2.9. Пример №9…………………………………………………………….…….7
3. Вычислить определённые интегралы…….…………………...………………9
3.1. Пример №10...…………………………...…………………………….…….9
3.2. Пример №11...………………………………………………...……….…...10
4. Вычислить несобственные интегралы или установить их расходимость.....10
4.1. Пример №12...…………………………...…………………………….…...10
4.2. Пример №13...………………………………………………...……….…...11
5. Выяснить сходимость несобственных интегралов………………………......12
5.1. Пример №14...…………………………...…………………………….…...12
5.2. Пример №15...………………………………………………...……….…...12
6. Найти площадь области, ограниченной линиями……………………………13
6.1. Пример №16...…………………………...…………………………….…...13
7. Найти длину дуги кривой.……………………………………….……………14
7.1. Пример №17...…………………………...…………………………….…...14
8. Заключение………………..……………………………...………………..…..16
9. Список использованной литературы…………………...……...……………..17
Введение
Контрольная работа №1 по дисциплине «Математика» выполняется после изучения глав «Неопределённый интеграл» и «Определённый интеграл». Контрольная работа содержит 17 задач.
Найти неопределённые интегралы.
Пример №1.
Решение:
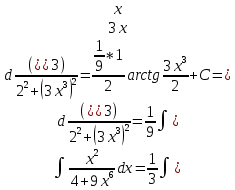
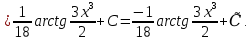
Пример №2.
Решение:
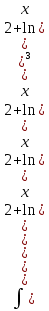
Пример №3.
Решение:
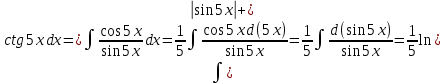
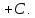
Пример №4.
Решение:
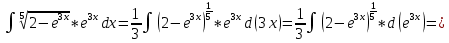
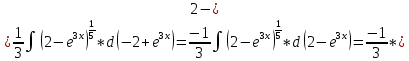
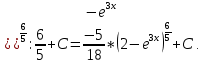
Пример №5.
Решение:
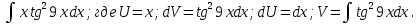
Находим V:
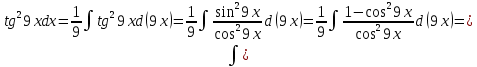
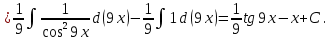
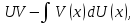
Следовательно:
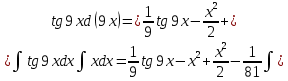
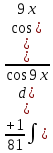
Пример №6.
Решение:
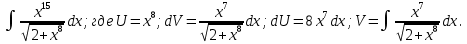
Находим V:
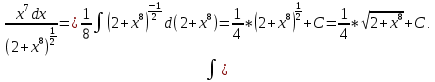
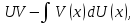
Следовательно:
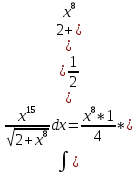
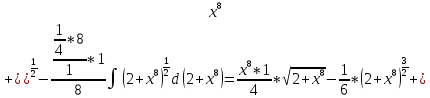
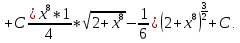
Пример №7.
Решение:
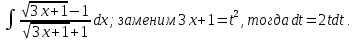
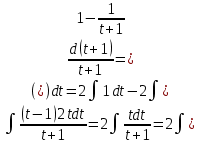
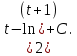
Следовательно:
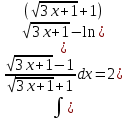
Пример №8.
Решение:
Преобразуем подынтегральную функцию:
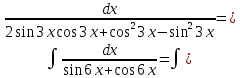
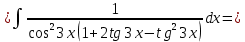
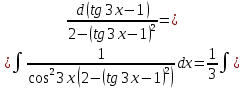
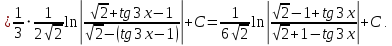
Пример №9.
Решение:
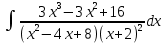
Разложим подынтегральную функцию на сумму простейших дробей:
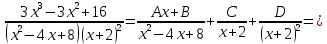
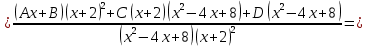
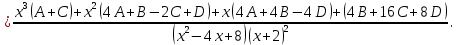
Коэффициенты
,
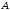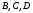найдем из условия: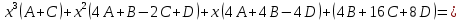
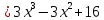. Приравняем коэффициенты с одинаковыми степенями при x:
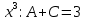
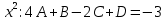
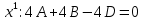
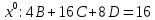
Откуда
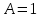
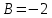
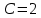
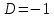
Таким образом,
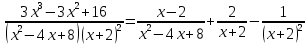
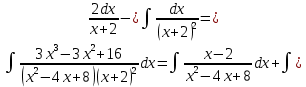
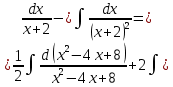
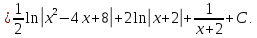
Вычислить определённые интегралы.
Пример №10.
Решение:
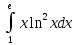
Применим формулу интегрирования по частям
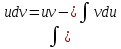
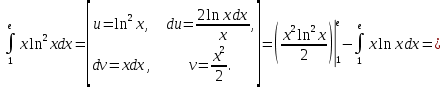
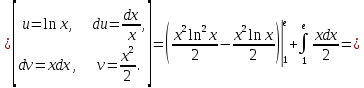
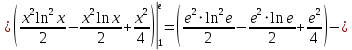
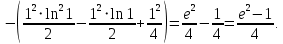
Пример №11.
Решение:
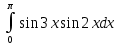
Применим тригонометрическую формулу произведения синусов:
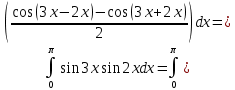
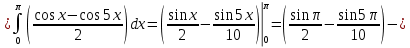
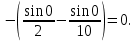
Вычислить несобственные интегралы или установить их расходимость.
Пример №12.
Решение:
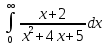
Это несобственный интеграл I рода (с бесконечным пределом интегрирования). Согласно определению несобственного интеграла I рода
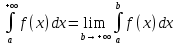
имеем
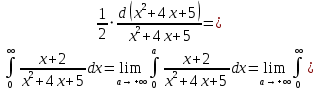
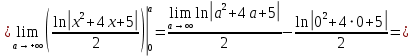
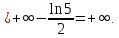
Ответ: интеграл расходится.
Пример №13.
Решение:
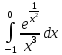
Это несобственный интеграл II рода. Согласно определению несобственного интеграла II рода
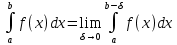
имеем
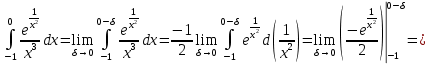
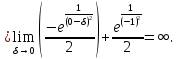Ответ: интеграл расходится.Выяснить сходимость несобственных интегралов.
Пример №14.
Решение:
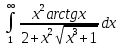
Так как на промежутке
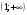имеет место неравенство: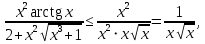
то имеем сопоставление интегралов в виде частного и общего признаков сравнения:
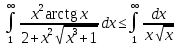
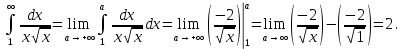
Поскольку интеграл в правой части неравенства сходится, то исследуемый интеграл тоже сходится согласно общему признаку сравнения несобственных интегралов.
Ответ: интеграл сходится.
Пример №15.
Решение:
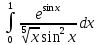
Так как при
:
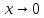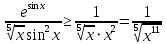то имеем сопоставление интегралов в виде частного и общего признаков сравнения: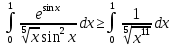 
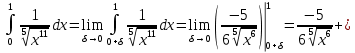
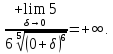
Поскольку данный интеграл расходится, то исследуемый интеграл тоже расходится согласно общему признаку сравнения несобственных интегралов.
Ответ: интеграл расходится.
Найти площадь области, ограниченной линиями.
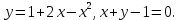
Пример №16.
Решение:
Координаты точек пересечения линий находим из системы:
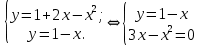
Отсюда:
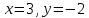и 
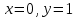.Строим заданные линии на плоскости ХOУ.
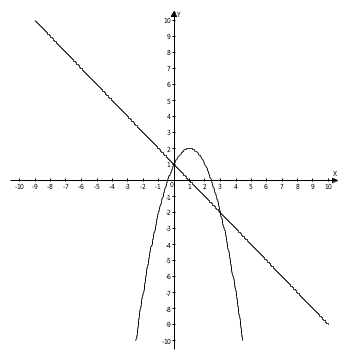
Составляем определенный интеграл:
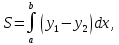
где
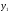– линия, ограничивающая область сверху; 
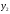– линия, ограничивающая область снизу; 
– наименьшее значение переменной x в области;