Файл: 1. Степень с рациональным показателем. Определение корня nой степени и его свойства.docx

1 . Степень с рациональным показателем. Определение корня n-ой степени и его свойства.

Степень с рациональным показателем — это степень в показателе которой находится конечная обыкновенная или десятичная дробь. Корнем n-ой степени из неотрицательного числа a (n=2, 3, 4...) называют такое неотрицательное число, при возведении которого в степень n получается число a.

Свойства:

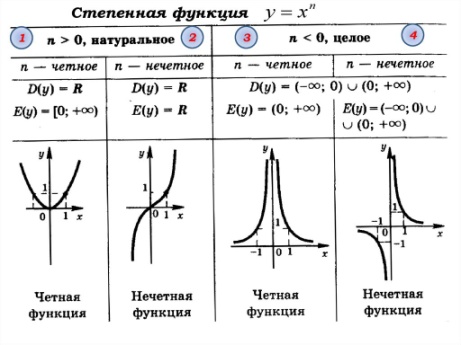
2 Степенная функция. График степенной функции, ее свойства.

Степенная функция – это функция вида f (x) = x^a, где: a – показатель степени, является действительным числом, a ≠ 0; x – основание степени, это свободная переменная.







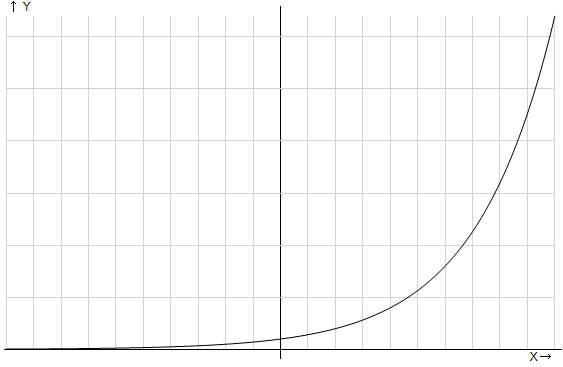
3 Показательная функция. Ее свойства, общий вид графика показательной функции (a > 1).





Нет минимума и максимума

Возрастает

4 Показательная функция. Ее свойства, общий вид графика показательной функции (0 < 1)



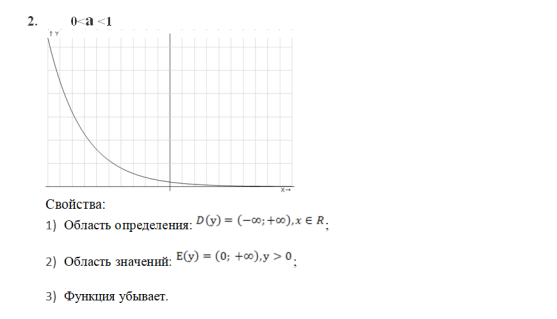
5 . Логарифм. Определение. Свойства.

Логарифмом числа b по основанию a называется показатель степени, в которую нужно возвести основание a, чтобы получить число b.





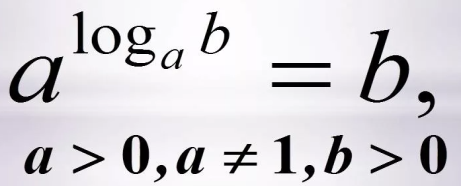
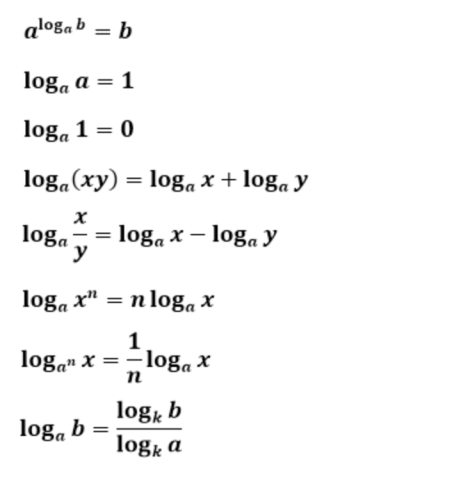
6 . Логарифмическая функция. Ее свойства, график (a > 1). Логарифмическая функция — это такая функция, которая записана в виде: y= log a x, где a и x больше нуля, при этом a≠1. 





7. Логарифмическая функция. Ее свойства, график (0 <а<1)



8 Определение основных понятий комбинаторики: перестановки, сочетания, размещения





Сочетаниями называют различные неупорядоченные комбинации элементов, которые выбраны из множества различных элементов, и которые отличаются друг от друга хотя бы одним элементом.



9 Определение события, вероятности события. Сложение и умножение вероятностей.

Сложение : P (A + B) = P (A) + P (B).

Умножение :  P (A × B) = P (A) × P a (B).

Вероятностью события называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. 

10 Формула Бернулли



11 Тригонометрические функции. Определение синуса, косинуса, тангенса, котангенса. y=sin x

У=cosx


У=tgx





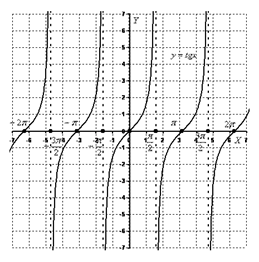
У=сtg







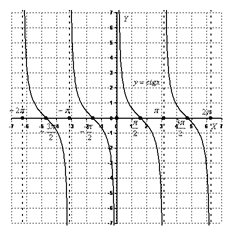
12 Радианная мера угла. Переход от градусной меры к радианной и наоборот.



13 Знаки синуса, косинуса, тангенса, котангенса. Синус, косинус, тангенс, котангенс углов α и −α..





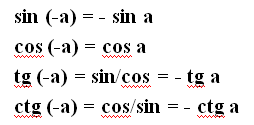
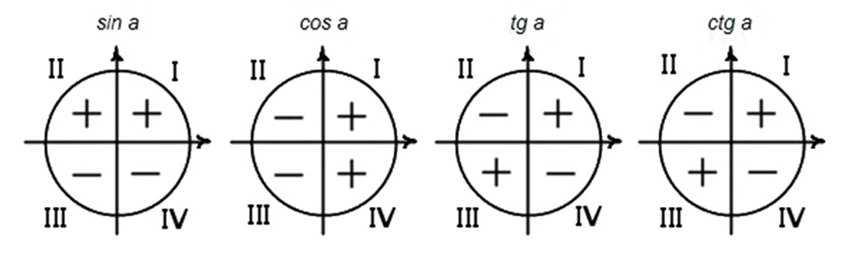
Синус – у (-)

Косинус-х (+)

14 Зависимость между тригонометрическими функциями одного угла.





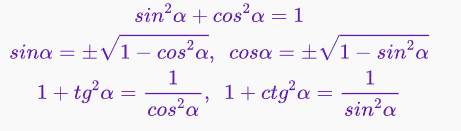
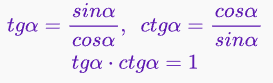
15 . Формулы двойного угла. Формулы сложения.

Формулы двойного угла











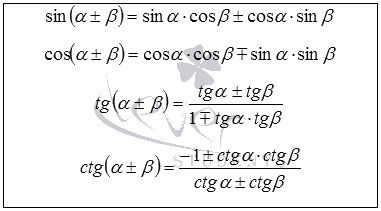
16. Правило приведения.



17 Уравнение cos x = α. Общий случай. Частные случаи.





18 Уравнение sin x = α. Общий случай. Частные случаи.



в

19У равнение tg x = α. Уравнение ctg x = α









20 Понятие arctg α. Arctg отрицательного значения. Понятие arcctg α. Arcctg отрицательного значения



21 Понятие arctg α. Arctg отрицательного значения. Понятие arcctg α. Arcctg отрицательного значения.

Арккотангенс числа a – это такое число альфа, которое принадлежит (0;П), котангенс которого равен a. Арктангенс числа a – это такое число альфа, которое принадлежит (-П/2;П/2), тангенс которого равен a.
arctg a = альфа, если tg альфа = a
альфа принадлежит (-П/2;П/2)

arctg (-a) = – arcctg a
x = arctg a + Пn
n принадлежит Z

arcctg a = альфа, если ctg альфа = a
альфа принадлежит (0;П)

arcctg (-a) = П – arcctg a
x = arcctg a + Пn
n принадлежит Z

22 Функция y = cos x, ее свойства, график





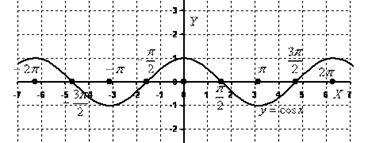
23 Функция y = sin x, ее свойства, график.





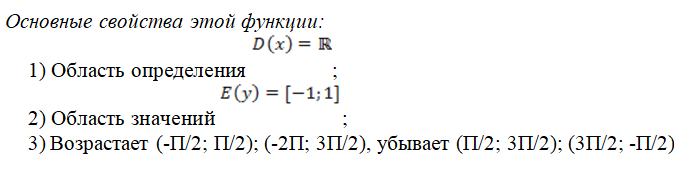
24. Функция y = tg x, ее свойства, график.





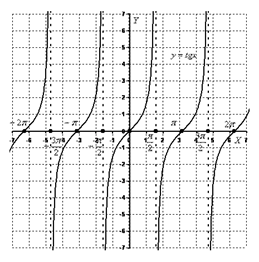
25 Функция y = ctg x, ее свойства, график.





26 . Производная функции, определение.

Производная функции – это предел отношения приращения функции к приращению аргумента, при условии, что приращение аргумента стремится к нулю.



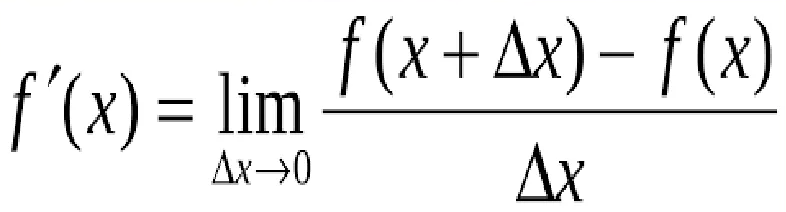
27 Правила дифференцирования





28 Геометрический смысл производной. Уравнение касательной к графику функции.





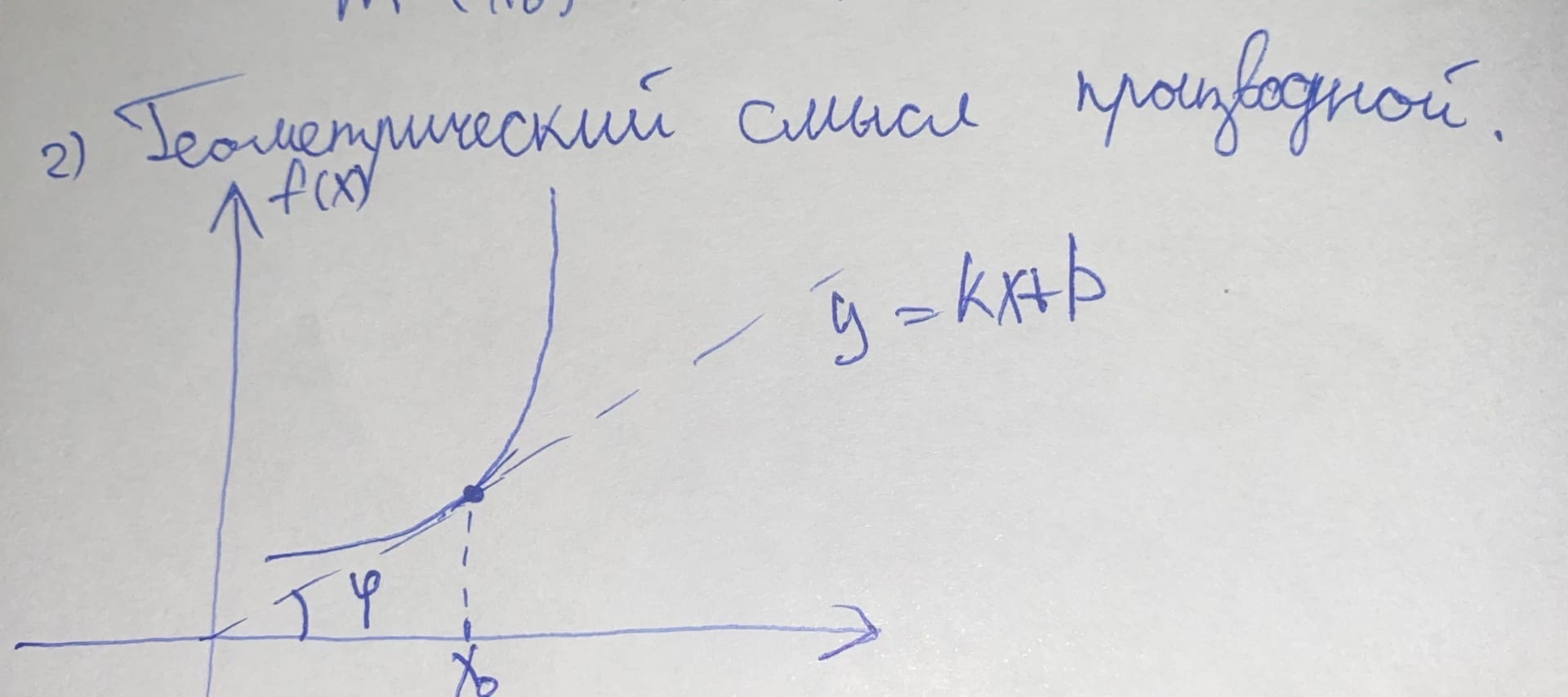
29. Исследование функции на убывание и возрастание





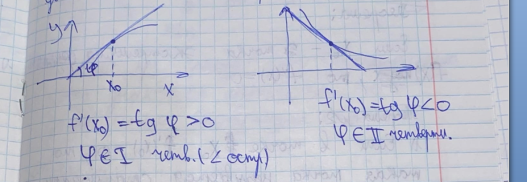
30 Точки экстремума и экстремумы функции. Исследование на точки экстремума и экстремум функции.





31 Предмет стереометрии. Аксиомы стереометрии. Следствия из аксиом стереометрии Основными фигурами стереометрии являются точка, прямая, плоскость. Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д. Аксиомы : 1) Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 



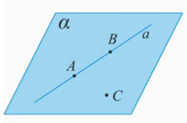
2) Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 





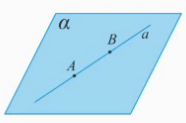
3) Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят, что плоскости пересекаются по прямой. 



32 Параллельные прямые в пространстве. Теорема о параллельных прямых.







33 Параллельность прямой и плоскости. Признак параллельности прямой и плоскости.



34 Взаимное расположение прямых в пространстве



35 Скрещивающиеся прямые. Признак скрещивающихся прямых

Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.



. 

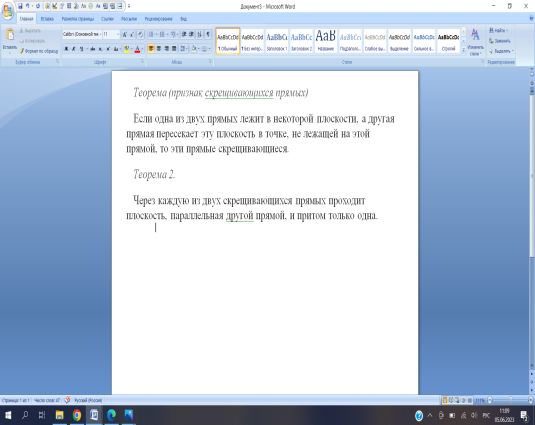
36. Угол между прямыми в пространстве.



37. Параллельные плоскости. Признак параллельности двух плоскостей
Две плоскости называются параллельными, если они не пересекаются.

Если две плоскости α и β параллельны, то пишут так:

 Признак: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум.

38 . Параллельные плоскости. Свойства параллельных плоскостей

1. 
   Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
   
2. 
   Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну
   
3. 
   Отрезки параллельных прямых, ограниченные двумя параллельными плоскостями, равны
   

Параллельные плоскости – плоскости, которые не пересекаются.

39 . Параллелепипед. Элементы параллелепипеда. Свойства параллелепипеда Параллелепипед — многогранник, у которого шесть граней и каждая из них параллелограмм. Элементы: 1.Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. 2.Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. 3.Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. 4.Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями. Свойства параллелепипеда: 1)противоположные грани параллелепипеда равны и параллельны 2)Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам 3)Боковые грани прямого параллелепипеда — прямоугольники

40 Перпендикулярные прямые в пространстве. Лемма о перпендикулярности двух параллельных прямых к третьей прямой



,



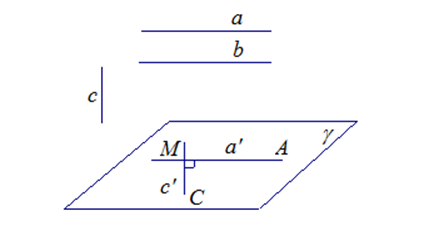
41 Перпендикулярность прямой и плоскости. Признак перпендикулярности прямой и плоскости

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.







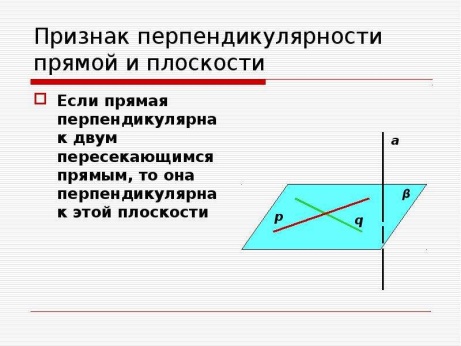
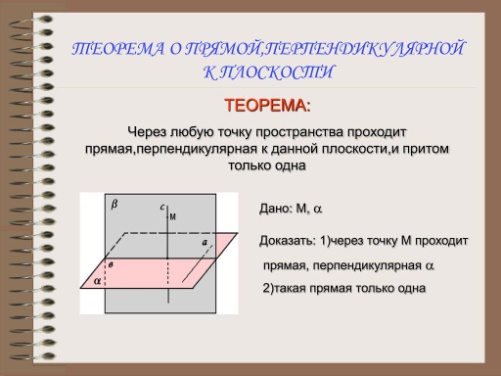
42 Перпендикуляр и наклонная. Расстояние от точки до плоскости, между параллельными плоскостями, прямой и параллельной ей плоскостью, между скрещивающимися прямыми.



43 Угол между прямой и плоскостью



44 Параллельные плоскости. Признак параллельности двух плоскостей.





45 Теорема о трех перпендикулярах. Двугранный угол. Перпендикулярность плоскостей



46 . Прямоугольный параллелепипед. Свойства прямоугольного параллелепипеда.





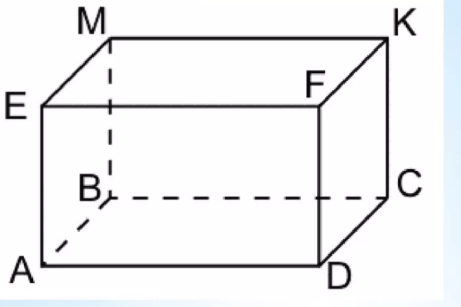
Свойства прямоугольного параллелепипеда:

1. 
   Все грани являются прямоугольниками.
   
2. 
   Противолежащие грани параллельны и равны друг другу.
   
3. 
   Две любые противолежащие грани могут быть приняты за основания.
   
4. 
   Грани пересекаются под углом 90°.
   
5. 
   Пересекающиеся ребра образуют прямой угол.
   

Объе




47 Декартова система координат на плоскости. Определение вектора, модуля вектор.

Для описания точек геометрических объектов с помощью чисел и написания уравнений задают систему координат. Существуют различные системы координат: декартова, полярная, криволинейная и другие. Будем рассматривать наиболее употребительную — декартову систему координат на плоскости.

Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.



48 Равенство векторов. Сложение векторов. Умножение вектора на число

Равенство векторов - Векторы называются равными, если они сонаправлены и их длины равны. 

Сложение (сумма) векторов «a + b» — это операция вычисления вектора c, все элементы которого равны попарной сумме соответствующих элементов векторов a и b, то есть каждый элемент вектора c равен: c=a+b.



49 Вычисление координат вектора, скалярного произведения векторов. Угол между векторами.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.

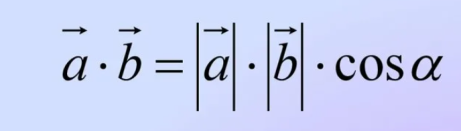
Углом между векторами называется угол между изображающими их направленными отрезками, отложенными от одной точки пространства.

50 Понятие многогранника. Правильные многогранники





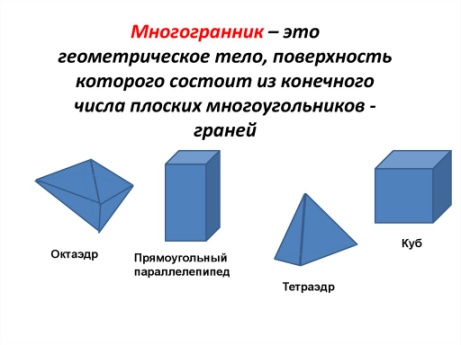
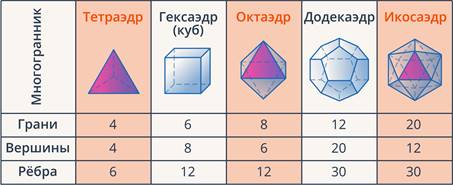
Правильный многогранник – выпуклый многогранник, все грани которого равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

51 Призма. Прямая и правильная призма.

При́зма - многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани — параллелограммами, имеющими общие стороны с этими многоугольниками.

А) Прямая призма — это призма, у которой боковые рёбра перпендикулярны плоскости основания, откуда следует, что все боковые грани являются прямоугольниками.

Б) Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.

52 Призма. Площадь боковой и полной поверхности призмы. Объем призмы
Объем - V = S*h





Призма имеет два основания. 

53 Пирамида. Правильная пирамида

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.


Пирамида называется правильной, если:

• 
  ее основание – правильный многоугольник;
  
• 
  отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
  

54 Пирамида. Площадь боковой и полной поверхности пирамиды. Объем пирамиды

Пирамида — многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

S полн = S бок + S осн

Площадь боковой поверхности :



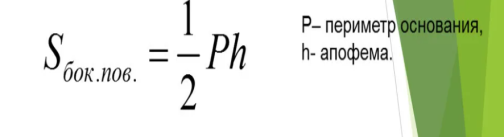
V= 1/3​Sh- объем

,,

55. Цилиндр. Основные сечения цилиндра.

Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

Осевое сечение цилиндра – прямоугольник, образованный в результате пересечения фигуры плоскостью, проходящей через ее ось.





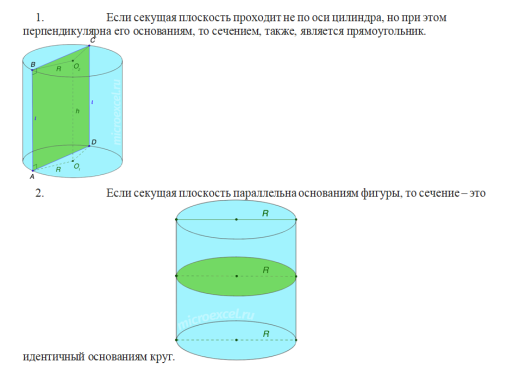
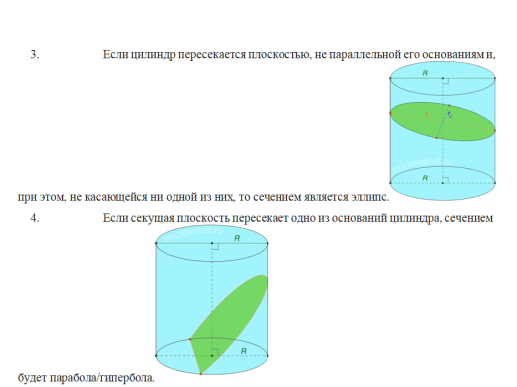
56 Цилиндр. Площадь поверхности и объем цилиндра





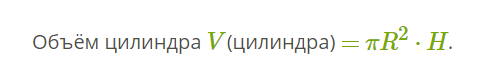
Цилиндр — геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.

57. Конус. Сечения конуса.

Конус — тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.



58 Конус. Площадь боковой и полной поверхности и объем конуса.

 S бок= πRl, где R – радиус основания, l – длина образующей. 

Площадь полной поверхности конуса находится по формуле: S кон= πRl + πR 2, где R – радиус основания, l – длина образующей

Объем конуса :

r- радиус , h-высота



59 Сфера, шар. Объем шара, площадь сферы



Площадь сферы





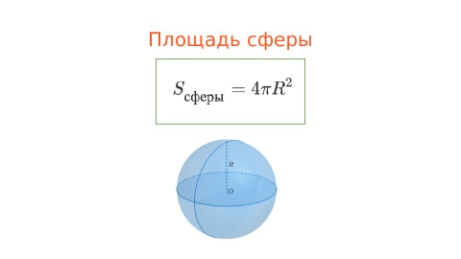
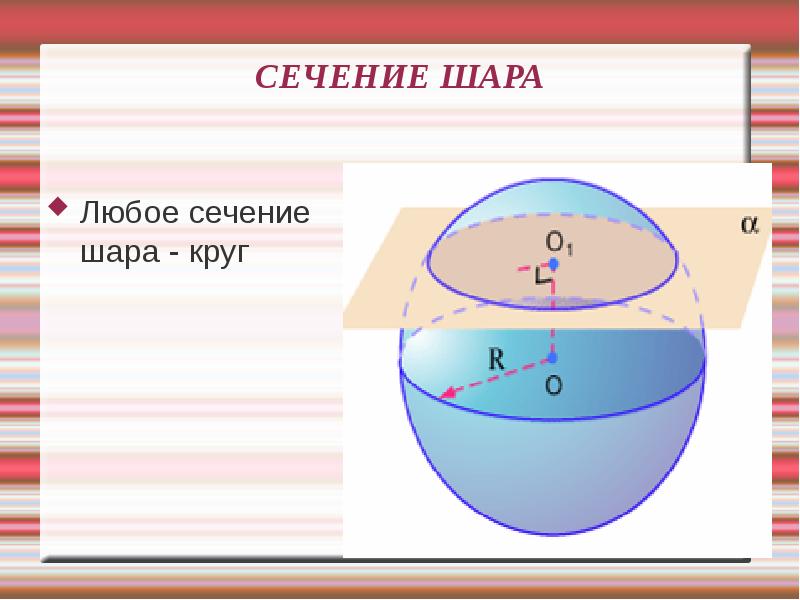
60 Сфера, шар. Сечения шара.

Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не большем данного R (R > 0). Данная точка называется центром шара, а данное расстояние R — радиусом шара.

Сферой называется множество всех точек пространства, находящихся от данной точки на расстоянии, равном данному R. Данные точка и расстояние R называются соответственно центром и радиусом сферы.