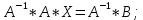Файл: Математические методы анализа процессов добычи нефти и газа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 198
Скачиваний: 7
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
Санкт-Петербургский горный университет
Кафедра разработки и эксплуатации нефтяных и газовых месторождений
МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ПРОЦЕССОВ ДОБЫЧИ НЕФТИ И ГАЗА
Методические указания к самостоятельным работам для студентов специальности 21.05.06
САНКТ-ПЕТЕРБУРГ
2019
УДК 622.276
МАТЕМАТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ПРОЦЕССОВ ДОБЫЧИ НЕФТИ И ГАЗА: Методические указания к самостоятельным работам / Санкт-Петербургский горный университет. Сост. Л.Р.Сагирова, А.Н.Паляницина. СПб, 2019. 14с.
Методические указания «Математические метода анализа процессов добычи нефти и газа» предназначены для самостоятельной подготовки студентов специальности 21.05.06 «Нефтегазовые техника и технологии», а также слушателей системы дополнительного профессионального образования в соответствии с учебным планом и программой дисциплины «Математические методы анализа процессов добычи нефти и газа».
Для обеспечения единого методического подхода к составлению проектных решений данные указания необходимо использовать при выполнении курсовых проектов студентами специальности 21.05.06 «Нефтегазовые техника и технологии».
Научный редактор: Зав. кафедрой РНГМ Горного университета, д.т.н., профессор М.К. Рогачев
Рецензент: к.т.н. Р.Р Гумеров главный специалист ООО «Газпромнефть НТЦ»
© Санкт-Петербургский
горный университет, 2019
ВВЕДЕНИЕ
Гидродинамическое моделирование это один из основных методов управления разработкой месторождения. Моделирование разработки нефтяных месторождений позволяет уточнить геологическое строение и фильтрационно-емкостные свойства нефтяного пласта при воспроизведении истории разработки. Одной из важнейших задач гидродинамического моделирования является прогнозирование технологических показателей разработки в средне- и долгосрочной перспективах, а также оптимизация систем разработки при различных методах воздействия на продуктивный пласт.
Разработка месторождений углеводородов представляет собой комплексную проблему, для успешного решения которой требуется привлечение знаний и опыта, накопленных в различных областях науки и инженерной практики. Применение комплексного мультидисциплинарного подхода стало особенно актуальным на современном этапе, характеризующемся, с одной стороны, существенным ухудшением структуры запасов нефти газа, а с другой – созданием принципиально новых технологий. Эти технологии распространены в области исследования и моделирования геологического строения пласта, бурения и заканчивания скважин, использованием новых быстродействующих компьютеров для проведения сложных вычислений, геологического и гидродинамического моделирования.
1. РАСЧЕТНО_ГРАФИЧЕСКОЕ ЗАДАНИЕ
Рассчитать распределение давления нефти в двухмерной модели пласта (Рис.1, Рис.2) используя неявный метод конечноразностного решения для 5 временных шагов.
| 1 | 2 | 3 | 4 |
| 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 |
Рис. 1 - Нумерация ячеек модели
| 30 | 30 | 30 | 30 |
| 30 | 40 | 40 | 40 |
| 30 | 40 | 40 | 50 |
| 30 | 40 | 50 | 40 |
Рис. 2 - Распределение проницаемости, мД
Граничные условия на границе залежи – отсутствие перетока. Свойства пласта и флюидов представлены в таблице 1.
Начальные и граничные условия представлены в таблице 2.
Таблица 1
Свойства пласта и нефти
| Ширина ячейки по оси х, м | 100 |
| Ширина ячейки по оси y, м | 100 |
| Толщина пласта, м | 50 |
| Объемный коэффициент нефти, м3/м3 | 1 |
| Вязкость нефти, мПас | 4 |
| Общая сжимаемость, 1/Па | 2.2∙10-9 |
| Пористость, % | 18 |
| Временной шаг, сут | 10 |
Таблица 2
Начальные и граничные условия
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 1 | 16 | 25 | 40 | 20 |
| 2 | 2 | 15 | 24 | 35 | 25 |
| 3 | 3 | 14 | 23 | 30 | 30 |
| 4 | 4 | 13 | 22 | 25 | 35 |
| 5 | 5 | 12 | 21 | 20 | 40 |
| 6 | 9 | 8 | 20 | 40 | 40 |
| 7 | 8 | 9 | 21 | 35 | 35 |
| 8 | 12 | 5 | 22 | 30 | 30 |
| 9 | 13 | 4 | 23 | 25 | 25 |
| 10 | 14 | 3 | 24 | 20 | 20 |
| 11 | 15 | 2 | 25 | 40 | 20 |
| 12 | 16 | 1 | 24 | 35 | 25 |
| 13 | 1 | 16 | 23 | 30 | 30 |
| 14 | 2 | 15 | 22 | 25 | 35 |
| 15 | 3 | 14 | 21 | 20 | 40 |
| 16 | 4 | 13 | 20 | 40 | 40 |
| 17 | 5 | 12 | 21 | 35 | 35 |
| 18 | 9 | 8 | 22 | 30 | 30 |
| 19 | 8 | 9 | 23 | 25 | 25 |
| 20 | 12 | 5 | 24 | 20 | 20 |
| 21 | 13 | 4 | 25 | 40 | 20 |
| 22 | 14 | 3 | 24 | 35 | 25 |
| 23 | 15 | 2 | 23 | 30 | 30 |
| 24 | 16 | 1 | 22 | 25 | 35 |
где: 1 – Номер варианта;
2 – Расположение добывающей скважины;
3 – Расположение нагнетательной скважины;
4 – Начальное пластовое давление, Мпа;
5 – Дебит добывающей скважины в поверхностных условиях, куб. м/сут;
6 – Расход нагнетательной скважины в поверхностных условиях, куб. м/сут.
Уравнение фильтрации для одномерного пласта:
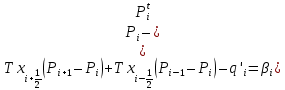 ,
, i=1, ……., N (1)
Уравнение фильтрации для двумерного пласта:
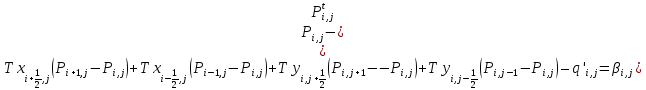
i=1, ……., N (2)
На рисунке 3 представлена модель двумерного пласта с корректной нумерацией ячеек.
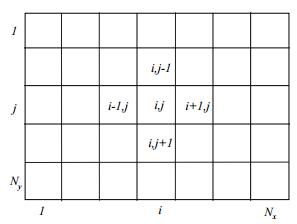
Рис. 3. Модель двумерного пласта
Уравнение фильтрации для двумерного пласта после преобразования принимает вид:
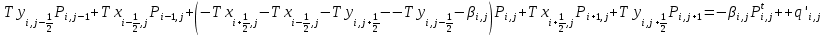 ; (3)
; (3)Для упрощения записи введем в уравнение коэффициенты выражения 4-10:
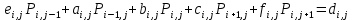 ; (4)
; (4)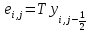 ; (5)
; (5)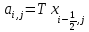 ; (6)
; (6)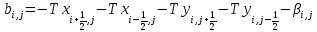 ; (7)
; (7)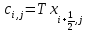 ; (8)
; (8)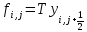 ; ; (9)
; ; (9)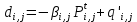 . ; (10)
. ; (10)Расчет конечно – разностной проводимости
Выражения для расчета конечно-разностной (11-14) проводимости для всех граней:
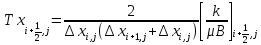 ; (11)
; (11)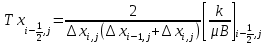 ; (12)
; (12) ; (13)
; (13)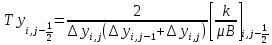 ; (14)
; (14)Для нахождения конечно-разностной проводимости на всех гранях ячеек нам необходимо разделить данный параметр на составляющие:
-
Геометрическая составляющая (выражение 15):
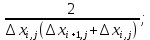
(15)
-
Проницаемость (k); -
Подвижность (выражение 16):
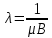 (16)
(16)Рассчитываем геометрическую составляющую, проницаемость на всех гранях ячеек, а также подвижность.
Гармоническая аппроксимация проницаемости:
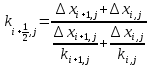 ; (17)
; (17)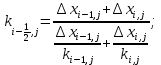 (18)
(18)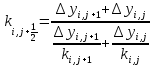 ; (19)
; (19)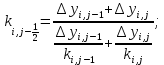 (20)
(20)Арифметическая аппроксимация подвижности рассчитывается из выражений 21-25:
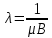 (21)
(21)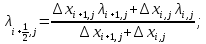 (22)
(22)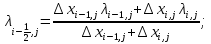 (23)
(23)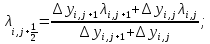 (24)
(24)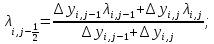 (25)
(25)Коэффициент упругоемкости пласта определяется из формулы 26:
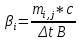 (26)
(26)Удельный дебит скважины при условии постоянного расхода:
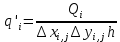 (27)
(27)Далее решаем данную задачу методом обратной матрицы.
Метод обратной матрицы используется при решении систем линейных алгебраических уравнений, если число неизвестных равно числу уравнений. Обратная матрица может быть найдена только для квадратной матрицы.
Суть метода.
Пусть задана система n линейных уравнений с nнеизвестными:
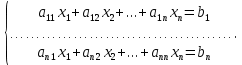 (28)
(28)Эту систему можно записать в виде матричного уравнения A*X=B,
где A=
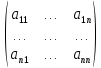 - матрица системы
- матрица системыX=
 – столбец неизвестных,
– столбец неизвестных,B=
 – столбец свободных коэффициентов.
– столбец свободных коэффициентов.Из полученного матричного уравнения необходимо выразить X. Для этого умножим обе части матричного уравнения слева на
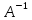 , получим:
, получим: