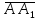Контрольная работа №3.Задание 1.Даны четыре точки пространства:А=(-4;2;6), В=(2;-3;0), С=(-10;5;8) D=(-5;2;4)В пирамиде ABCD найти№1 Длину ребра АВ;№2 Общее уравнение грани АВС;№3 Уравнение грани АВС в отрезках;№4 Уравнение плоскости, проходящей через вершину D параллельно грани АВС;№5 Угол между ребрами АВ и ВС;№6 Величину двугранного угла при ребре ВС;№7 Угол между ребром АВ и гранью ВСD№8 Каноническое и параметрическое уравнение ребра АВ№9 Уравнение высоты опущенной из вершины А на плоскости ВСD;№10 Длину высоты , опущенной из вершины D на плоскости АВС;№11 Площадь грани АВС;№12 Объем пирамиды по высоте и площади основания;№13 Объем пирамиды с помощью смешанного произведения;№1.Найти длину ребра АВА=(-4;2;6), В=(2;-3;0)d=|ĀВ|=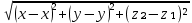d=|ĀB|= 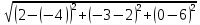= = 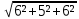= =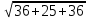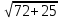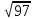d= 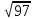=9,85№2.Найти общее уравнение грани АВС. Решить уравнение плоскости в пространстве по трем точкам. 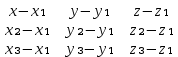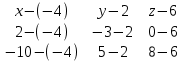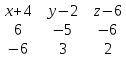=0A=(-4; 2; 6) В=(2; -3; -0) С=(-10; 5; 8) =0 =0((x+4)*(-5)*2+(y-2)*(-6)*(-6)+(6*3*(z-6))-((z-6)*(-5)(-6)+(y-2)*6*2+(x+4)*3(-6))=0-10(x+4)+36(y-2)+18(z-6)-(30(z-6)+12(y-2)-18(x+4))=0-10x-40+36y-72+18z-108-(30z-108+12y-24-18x-72=0)-10x+36y+18z-220-30z-12y+18x276=08x+24y-12z+56=0(8(x+4)+24(y-2)-12(z-6)=0) 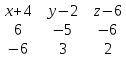=-10(x+4)+36(y-2)+18(z-6)-(30(z-6)+12(y-2)-18(x+4))=-10(x+4)+36(y-2)+18(z-6)-30(z-6)-12(y-12)+18(x+4)=8(x+4)+24(y-2)-12(z-6)=0№3 Уравнение грани АВС в отрезках + +

---

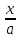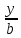=1 8x+24y-12z+56=0

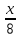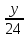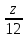+ - =1 a=8, b=24, c=-12

№4. Уравнение плоскости, проходящей через вершину D параллельно грани АВС.

Решение: 8(x+4)+24(y-2)-12(z-6)=0

Уравнение плоскости

8(x+4)+24(y-2)-12(z-6)=0

D=(-5; 2; -4)

Составим уравнение связки плоскостей, проходящих через точку D=(-5; 2; -4)

А(x+5)+B(y-2)+C(Z+4)=0

Плоскости параллельны, если пропорциональны коэффициенты при x,y,z.

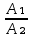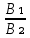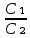= = =K, то А₁=А; В₁=В; С₁=С; А₂=8; В₂=24; С₂=-12.

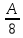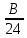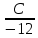= = = K, пусть K=1, то A=8, B=24, C=-12, уравнение плоскости. Проходящей через вершину D параллельно грани ABC

8(x+5)+24(y-2)-12(z+4)=0 или 8(x+5)+24(y-2)-12(z+4)=8x+40+24y-48-12z-48=8x+24y12z-56=8x+24y-12z-56=0

№5. Угол между ребрами AB и BC

Решение:

Cos( ^ )=

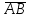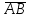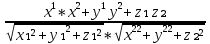
A=(-4; 2; 6) B=(2; -3; 0) C=(-10; 5; 8)

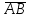= (2-(-4); -3-2; 0-6) 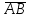= (6; -5; -6)

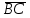= (-10-12; 5-(-3); 8-0) 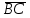= (-12; 8; 8)

Cos( ^ ) = = = = = =

---

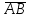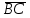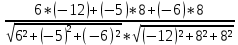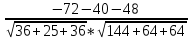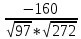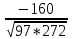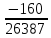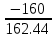
=-0.98,

arccos(-0.98)=(AB^BC)=2.94°

№6. Величину двугранного угла при ребре BC.

Решение: D

Двугранный угол при ребре ВС – есть угол между

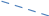плоскостями (АВС) и (DВС). Найдем их A B

уравнение.

C

A=(-4;2;6), B=(2;-3;0), C=(-10; 5; 8), D= (-5; 2; -4)

(ABC): 8x+24y-12z+56=0 общий вид уравнения

(DBC): 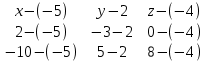=0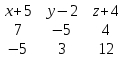 =0

=0

((x+5)*(-5)*12+(y-2)*4*(-5)+(z+4)*7*3)-((z+4)*(-5)*(-5)+(y-2)*7*12+(x+5)*4*3)=-60*(x+5)-20(y-2)+21(z+4)-(25(z+4)84(y-2)+12(x+5))=-60(x+5)-20(y-2)+21(z+4)-25(z+4)+84(y-2)+12(x+5)=-48(x+5)+64(y-2)-4(z+4)=-48x-240+64y-128-4z-16=-48x+64y-4z-264=0

(DBC): -48x+64y-4z-264=0

(ABC): 8x+24y-12z+56=0

n₁=(8;24;-12) – проекция вектора перпендикулярного плоскости DBC.

Величина двугранного угла – есть величина линейного угла между проекциями n₁ и n₂.

Cos(n₁^n₂)= ;

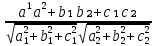Cos( 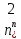)= =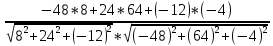 = = 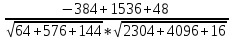= = 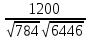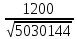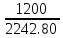0.54

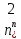arccos0.54=1.00

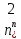1

№7 Угол между ребром АВ и гранью BCD

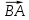=(-4-2; 2-(-3); 6-0).

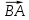=(-6; 5; 6)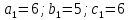

---

(BCD):-48x+64y-4z-264=0



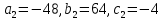
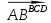( )=arcsin4

Sin4=

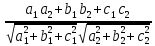
Sin4= 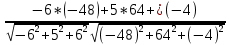= = 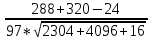= = 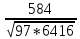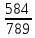0.7402

Arcsin4 0.7402=

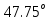
4=47.

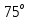
№8 Каноническое и параметрическое уравнения ребра AB.

A=(-4; 2; 6) B=(2; -3; 0)

Решение:

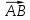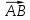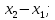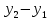=(2-(-4); -3-2; 0-6), =(6; -5; -6), тогда проекции вектора m= n= ; p=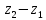

= =

= =

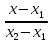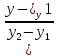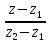
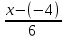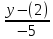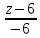
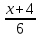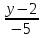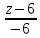= = – каноническое уравнение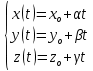

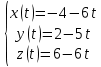- параметрическое уравнение

=

=

=

---

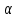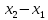
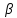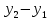
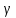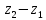
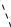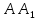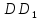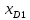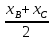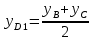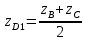
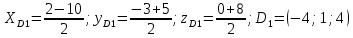
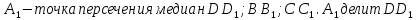
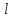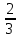
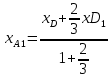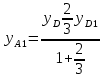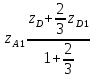
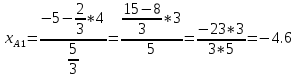
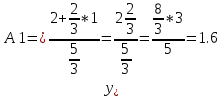
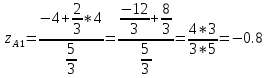
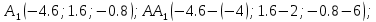
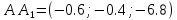
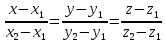
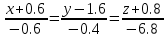
№9 Уравнение высоты, из вершины А на плоскость BCDAA=(-4; 2; 6) Решение: D B ⊥(BCD) CB=(2; -3; 0) C=(-10; 5; 8) D=(-5; 2; -4) – медиана, то = ; ; 2:1 считая от D.λ= ; ; №10(

---

Смотрите также файлы

• Лабораторная работа Командные файлы Цель научиться создавать командные файлы Краткие теоретические сведения.docx

• Установленный лимит остатка денежных средств в кассе 2000 рублей.docx

• В словари за частями речи.doc

• Темы докладов к лекциям 1 и 2.docx

• Тема 11. 9.doc