Файл: Контрольная работа 3. Задание Даны четыре точки пространства А(426), В(230), С(1058) D(524).docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 49
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
)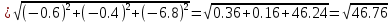 = 6.84
= 6.84
№11.
Площадь грани ABC, A(-4; 2; 6); B=(2;-3;0); C=(-10; 5; 8)
 Решение: D
Решение: D

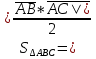 B
B
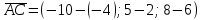 A C
A C
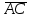 =(-6(
=(-6(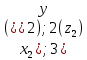 )
)
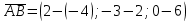
 =(6(
=(6(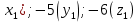 )
)
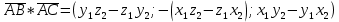
|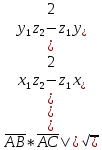
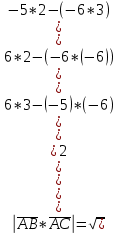 =
=
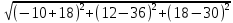 =
=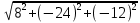 =
=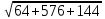 =
=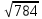 =28
=28
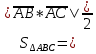 =
=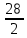 =14
=14
№13. Найти объем пирамиды с помощью смешанного произведения с вершинами A(-4; 2; 6), B(2; -3; 0), C(-10; 5; 8), D(-5; 2; -4).
Решение:
Составим образующие пирамиду векторы, взяв точку А начальной:
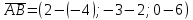
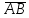 =(6; -5; -6)
=(6; -5; -6)
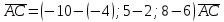 =(-6; 3; 2)
=(-6; 3; 2)
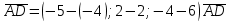 =(-1; 0; -10)
=(-1; 0; -10)
Найдем смешанное произведение векторов
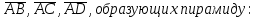
(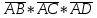 )=
)=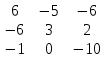 = (6*3*(-10)+(-5)*2*(-1)+(-6)*0*(-6))-
= (6*3*(-10)+(-5)*2*(-1)+(-6)*0*(-6))-
-(-6*3*(-1)+(-5)*(-6)*(-10)+2*0*6)=(-180+10+0)-(18-300+0)=-180+10-18+300=120-8=112
Знак «+» показывает, что при данном порядке векторов тройка правая
V=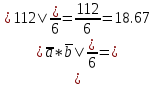
№12.
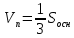 *h
*h
h=A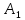 из n 9.10
из n 9.10
h=6.84
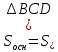
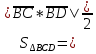 B=(2; -3; 0) C=(-10; 5; 8) D=(-5; 2; -4)
B=(2; -3; 0) C=(-10; 5; 8) D=(-5; 2; -4)
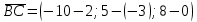
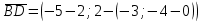
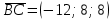
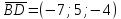
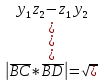
|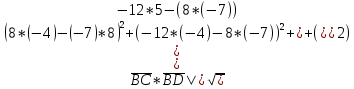 =
=
=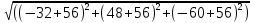 =
=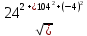 =
=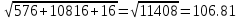
S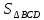 =
=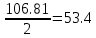
Vnn=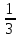
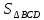 =
=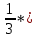 53.4*6.84=121.75
53.4*6.84=121.75
Задание №2.
Изобразить кривую, заданную уравнением
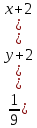 . Определить для кривой полуоси фокусное расстояние, эксцентриситет, координаты центра и фокусов.
. Определить для кривой полуоси фокусное расстояние, эксцентриситет, координаты центра и фокусов.
Решение:
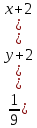
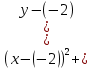
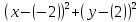 =
=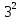 - окружность
- окружность
С(-2; -2) – центр окружности r=3
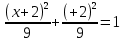
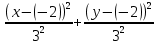 =1 эллипс
=1 эллипс
а=3, b=3 – полуоси
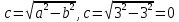 – фокусное расстояние
– фокусное расстояние
(-2; -2) - центр
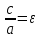
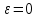 –эксцентрисистент окружности частный дну эллипса. Фокус совпадает с центром.
–эксцентрисистент окружности частный дну эллипса. Фокус совпадает с центром.
Полуоси равны 3*2=6.
Задание №3.
Изобразить кривую, заданную уравнением
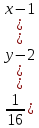 . Определить вид кривой полуоси, фокусное расстояние, эксцентриситет, координаты центра и фокуса.
. Определить вид кривой полуоси, фокусное расстояние, эксцентриситет, координаты центра и фокуса.
Решение:
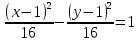
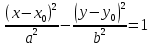 - уравнение гиперболы
- уравнение гиперболы
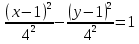 – гипербола
– гипербола
a=b=4 – полуоси
с=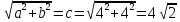 – фокусное расстояние, (1; 1) – центр.
– фокусное расстояние, (1; 1) – центр.
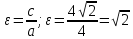 – эксцентриситет гиперболы
– эксцентриситет гиперболы
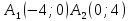 – точки пересечения с осью 0x. Ось ординат гипербола не пересекает.
– точки пересечения с осью 0x. Ось ординат гипербола не пересекает.
y=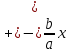 – асимптоты гиперболы
– асимптоты гиперболы
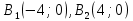 -линейные точки пересечения с осью 0y
-линейные точки пересечения с осью 0y


 y
y







 4
4 









 -6 -4
-6 -4  0
0 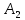 6 x
6 x
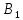
X=6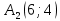
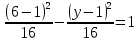
25-(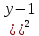 =16
=16
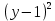 =9
=9
y-1=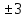
y=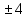
Задание №4.
Привести уравнение кривой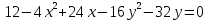 к каноническому виду. Построить линию, заданную уравнением.
к каноническому виду. Построить линию, заданную уравнением.
Решение:
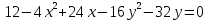
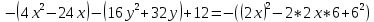 -
-
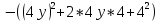 +12+36+16=
+12+36+16=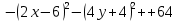 =
=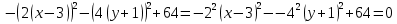
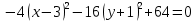
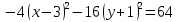 (
(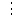 (-64))
(-64))
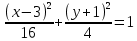 – эллипс
– эллипс
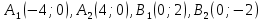
вершины эллипса
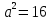 , a=4
, a=4
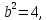 b=2
b=2
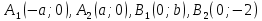 – вершины эллипса.
– вершины эллипса.
Задание №5.
Привести уравнение кривой
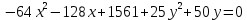 к каноническому виду. Построить линию, заданную уравнением.
к каноническому виду. Построить линию, заданную уравнением.
Решение:
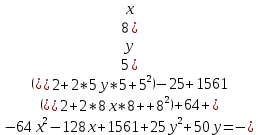 =
=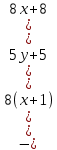
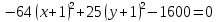
-64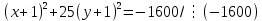
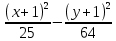 =1
=1
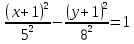 – гипербола
– гипербола
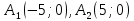 – пересечение с 0x
– пересечение с 0x
 – линии пересечения с 0y
– линии пересечения с 0y
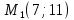
X=7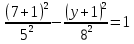
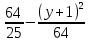 =1
=1
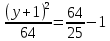
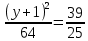
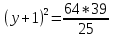
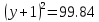
y+1=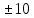
y=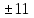
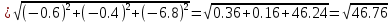 = 6.84
= 6.84№11.
Площадь грани ABC, A(-4; 2; 6); B=(2;-3;0); C=(-10; 5; 8)
 Решение: D
Решение: D
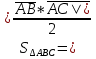 B
B
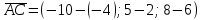 A C
A C  =(-6(
=(-6(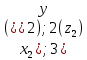 )
)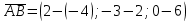
 =(6(
=(6(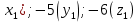 )
)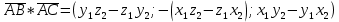
|
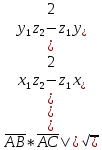
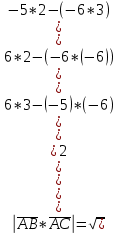 =
=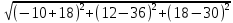 =
=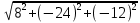 =
=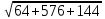 =
=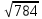 =28
=28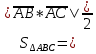 =
=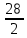 =14
=14№13. Найти объем пирамиды с помощью смешанного произведения с вершинами A(-4; 2; 6), B(2; -3; 0), C(-10; 5; 8), D(-5; 2; -4).
Решение:
Составим образующие пирамиду векторы, взяв точку А начальной:
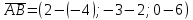
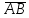 =(6; -5; -6)
=(6; -5; -6)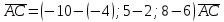 =(-6; 3; 2)
=(-6; 3; 2)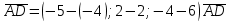 =(-1; 0; -10)
=(-1; 0; -10)Найдем смешанное произведение векторов
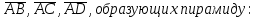
(
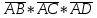 )=
)=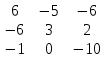 = (6*3*(-10)+(-5)*2*(-1)+(-6)*0*(-6))-
= (6*3*(-10)+(-5)*2*(-1)+(-6)*0*(-6))--(-6*3*(-1)+(-5)*(-6)*(-10)+2*0*6)=(-180+10+0)-(18-300+0)=-180+10-18+300=120-8=112
Знак «+» показывает, что при данном порядке векторов тройка правая
V=
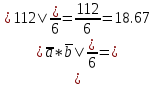
№12.
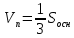 *h
*hh=A
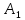 из n 9.10
из n 9.10h=6.84
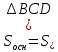
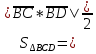 B=(2; -3; 0) C=(-10; 5; 8) D=(-5; 2; -4)
B=(2; -3; 0) C=(-10; 5; 8) D=(-5; 2; -4)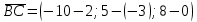
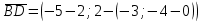
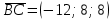
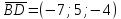
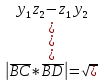
|
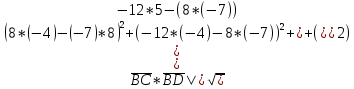 =
==
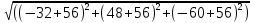 =
=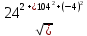 =
=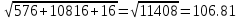
S
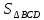 =
=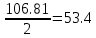
Vnn=
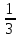
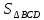 =
=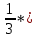 53.4*6.84=121.75
53.4*6.84=121.75Задание №2.
Изобразить кривую, заданную уравнением
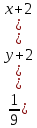 . Определить для кривой полуоси фокусное расстояние, эксцентриситет, координаты центра и фокусов.
. Определить для кривой полуоси фокусное расстояние, эксцентриситет, координаты центра и фокусов.Решение:
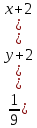
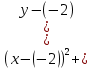
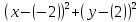 =
=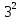 - окружность
- окружностьС(-2; -2) – центр окружности r=3
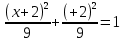
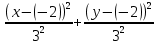 =1 эллипс
=1 эллипса=3, b=3 – полуоси
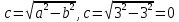 – фокусное расстояние
– фокусное расстояние(-2; -2) - центр
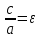
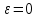 –эксцентрисистент окружности частный дну эллипса. Фокус совпадает с центром.
–эксцентрисистент окружности частный дну эллипса. Фокус совпадает с центром.Полуоси равны 3*2=6.
Задание №3.
Изобразить кривую, заданную уравнением
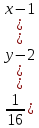 . Определить вид кривой полуоси, фокусное расстояние, эксцентриситет, координаты центра и фокуса.
. Определить вид кривой полуоси, фокусное расстояние, эксцентриситет, координаты центра и фокуса.Решение:
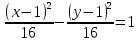
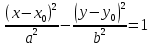 - уравнение гиперболы
- уравнение гиперболы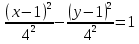 – гипербола
– гиперболаa=b=4 – полуоси
с=
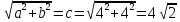 – фокусное расстояние, (1; 1) – центр.
– фокусное расстояние, (1; 1) – центр.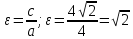 – эксцентриситет гиперболы
– эксцентриситет гиперболы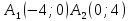 – точки пересечения с осью 0x. Ось ординат гипербола не пересекает.
– точки пересечения с осью 0x. Ось ординат гипербола не пересекает.y=
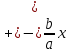 – асимптоты гиперболы
– асимптоты гиперболы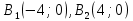 -линейные точки пересечения с осью 0y
-линейные точки пересечения с осью 0y

 y
y






 4
4 









 -6 -4
-6 -4  0
0  6 x
6 x
X=6
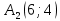
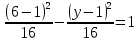
25-(
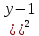 =16
=16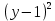 =9
=9y-1=
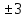
y=
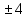
Задание №4.
Привести уравнение кривой
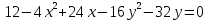 к каноническому виду. Построить линию, заданную уравнением.
к каноническому виду. Построить линию, заданную уравнением.Решение:
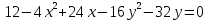
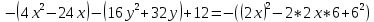 -
-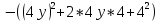 +12+36+16=
+12+36+16=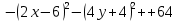 =
=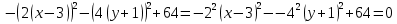
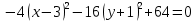
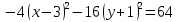 (
(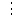 (-64))
(-64))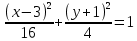 – эллипс
– эллипс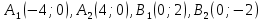
вершины эллипса
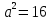 , a=4
, a=4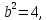 b=2
b=2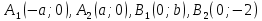 – вершины эллипса.
– вершины эллипса.Задание №5.
Привести уравнение кривой
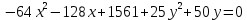 к каноническому виду. Построить линию, заданную уравнением.
к каноническому виду. Построить линию, заданную уравнением.Решение:
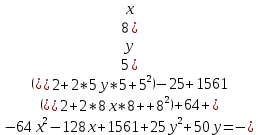 =
=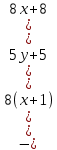
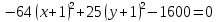
-64
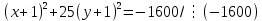
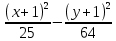 =1
=1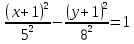 – гипербола
– гипербола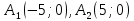 – пересечение с 0x
– пересечение с 0x – линии пересечения с 0y
– линии пересечения с 0y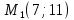
X=7
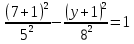
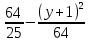 =1
=1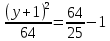
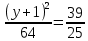
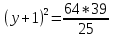
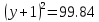
y+1=
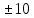
y=