Лекция №1
Множества и операции над ними.

Понятие множества

Людям постоянно приходится иметь дело с различными совокупностями предметов, что повлекло за собой возникновение понятия числа, а затем и понятия множества, которое является одним из основных простейших математических понятий.

Теория множеств – это раздел математики, в котором изучаются общие свойства множеств.

Основатель научной теории множеств – немецкий математик

Георг Кантор.

Определение. Множеством называется совокупность, набор и т. д. однотипных элементов, воспринимаемых как единое целое.

Множества обозначают большими латинскими буквами. Например,
А = {Коля, Петя, Маша, Ира}, В = {1, 2, 7}, С = {1, 2, 3, 4, …, n, …}.

Все предметы, составляющие множества, называются элементами множества. Элементы множества обозначают маленькими латинскими буквами. Например, если элемент х принадлежит множеству К, то пишут
х 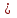К, если элемент х не принадлежит множеству К, то пишут х 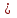К.

Есть множество, в котором нет ни одного элемента. Его называют пустым множеством и обозначают Ø.

Множество может быть конечным, если оно состоит из конечного числа элементов, и бесконечным, если оно содержит бесконечно много элементов. Примером конечного множества может служить множество дней недели, примером бесконечного множества – множество натуральных чисел.

Из школьного курса вам известны примеры бесконечных числовых множеств – множеств натуральных(N), целых(Z), рациональных(Q), иррациональных(I) и действительных чисел (R).

Множество может быть задано:

• 
  перечислением. Например, К = {2, 4, 20, 40};
  
• 
  характеристическим свойством, т.е. свойством, характерным только для элементов этого множества. Например, .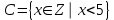
  

Из элементов множества А = {Коля, Петя, Маша, Ира}, например, можно составить новое множество М = {Петя, Маша}. Оно характеризуется тем, что все элементы М принадлежат множеству

---

А. Говорят, что М – подмножество множества А и пишут М А.

Множество М является подмножеством множества А, если всякий элемент множества М является элементом множества А и обозначают
М А.
Например, множество всех первокурсников является подмножеством множества всех студентов.


Для любого множества А справедливо:

1. 
   Само множество является своим подмножеством, т.е. А А.
   
2. 
   Пустое множество является подмножеством любого множества, т.е. Ø А.
   

Пример:

Сколько можно составить подмножеств множества В?

1. 
   В = {0, 1}, тогда {0} В, {1} В, Ø В, {0, 1} В – четыре.
   
2. 
   В = {1, 2, 3}, тогда {1} В, {2} В, {3} В, {1, 2} В, {1, 3} В,
   {2, 3} В, Ø В, {1, 2, 3} В – восемь.
   

Можно доказать, что если в множестве n элементов, то оно имеет
2ⁿ подмножеств.

Множества считаются равными, если они состоят из одних и тех же элементов. А также множества А и В равны, если А В и В А.

Пусть А={2, 1, 3}, a В = {1, 2, 3} тогда А= В.
Примеры.

1) Пусть А – множество канцелярских товаров в аудитории, В –множество шариковых ручек в аудитории, тогда B ⊂ A.

2) Перечислим все подмножества множества A = {1; 2; 3}:

---

{1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3}, {1; 2; 3}, ∅ .

Замечания.

1. Если A = B , то B 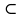A, A⊂ B.

2. Пустое множество является подмножеством любого множества: ∅ ⊂ A.

3. Знак ⊂ можно ставить только между множествами: B ⊂ A,

∅ ⊂ A.

4. Знак ∈ можно ставить только между элементом множества и

самим множеством: a∈{a; b; c}.

Операции над множествами, их свойства

Пусть все рассматриваемые множества являются подмножествами некоторого фиксированного множества, которое назовём универсальным и обозначим буквой U. Для геометрической иллюстрации операций над множествами воспользуемся диаграммами Эйлера – Венна, на которых универсальное множество изображают в виде прямоугольника, а остальные множества – в виде овалов, в частности кругов. Введём операции над множествами.
1. Бинарные операции

1.1. Пересечение множеств.

Пересечением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат как множеству А, так и множеству В и обозначают: A∩B. Таким образом, по определению, можно записать:
А∩В={x | (x ∈A) 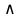(x∈ B)}


С помощью диаграмм Эйлера - Венна пересечение множеств обозначают:


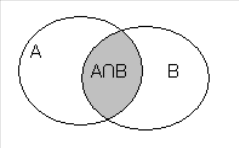
Рисунок 1. Пересечение множеств.

1. Пересечение любых множеств А и В всегда существует, и оно единственно.

2. Говорят, что пересечение множеств А и В пусто, если они не имеют общих элементов и пишут: А∩В=Ø.

3. А∩Ø=Ø.


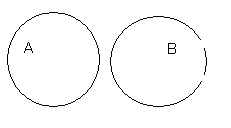
Рисунок 2. Пустое пересечение множеств


1.2. Объединение множеств.

Объединением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств А
и В и обозначают AUB. Таким образом, по определению:

A U B={x | (x ∈ А) (х ∈ В)}

С помощью диаграмм Эйлера - Венна объединение

множеств обозначают:

---

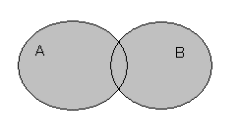
Рисунок 3. Объединение множеств А и В

1. Объединение любых множеств А и В всегда существует, и оно единственно.

2. AUØ=A.


1.3. Разность множеств.



Разностью множеств А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В.
Разность множеств А и В обозначают А\В. Таким образом, по определению:

A\B={x|(x ∈ A) (x B)}

С помощью диаграмм Эйлера - Венна разность множеств

обозначают:


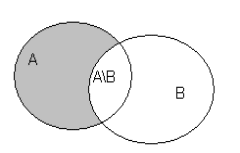
Рисунок 4. Разность множеств А и В

С помощью кругов Эйлера можно доказать следующие свойства множеств, справедливые для произвольных множеств А, В, С и D:

1) 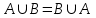(коммутативность объединения);

2) 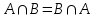(коммутативность пересечения);

3) 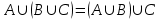(ассоциативность объединения);

4) 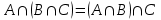(ассоциативность пересечения);

5) 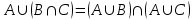(дистрибутивность объединения);

6) 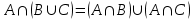(дистрибутивность пересечения);

1.4. Декартово произведение множеств.
Декартовым (или прямым) произведением множеств А и В называется — множество, элементами которого являются все возможные упорядоченные пары элементов исходных двух множеств А и В:

АхВ ={(x,y)|(x ∈ A) (y ∈ B)}

Пример:

если А={a₁,a₂} и B={b₁,b₂,b₃},
то АхВ ={(a₁,b₁), (a₁,b₂), (a₁,b₃), (a₂,b₁), (a₂,b₂), (a₂,b₃)}
2. Унарные операции.

2.1. Дополнение множества
Разностьмежду универсальным множеством U и множеством В называется дополнением множества В.

---

Обозначается CВ=U\В={x | x В)}


Рисунок 5. Дополнение множества В до универсального множества.

Пусть В А. Дополнением множества В до множества А называется множество, содержащее все элементы множества А, которые не принадлежат множеству В.

CB={x|(x ∈ A) (x B)}

Вычитание множества А и В в случаях, когда одно из них является подмножеством другого, называется дополнением множества В до
множества А.

С помощью диаграмм Эйлера-Венна дополнение множества В до множества А обозначают:

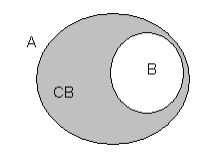
Рисунок 6. Дополнение множества В до множества А.

2.2. Мощность множества

Обозначим число элементов конечного множества А символом n(А) – это мощностьданного множества.

Например, если A={m ,p, r, s}, то можно записать, что n(А)=4, и сказать, что мощность множества А равна 4 или в множестве А четыре элемента.

Правило суммы.



- Если множество А содержит m элементов, а множество В - n элементов, и эти множества не пересекаются, то AUB содержит m+n элементов.

n(AUB)=n(A)+n(B), когда А∩В=Ø


- Если пересечение конечных множеств А∩В 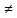Ø, то число элементов в объединении множеств равно разности между суммой чисел элементов множеств А и В и числом элементов в пересечении этих множеств.

n(AUB)=n(A)+n(B)-n(A∩B) при А∩В 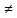Ø

Пример:

В бригаде 25 человек. Среди них 20 моложе 30 лет, 15 старше 20 лет. Может ли так быть?

Решение: Может! Пусть А –множество членов бригады моложе 30 лет. В –множество членов бригады старше 20 лет. С –множество всех членов бригады. С = А 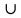В. Так как 20+15 >25, то А В ≠ Ø.

---

Смотрите также файлы

• Вопросы Укажите основные этапы эконометрического исследования.docx

• Группы орфограмм 5 класса.docx

• Введение Организационноуправленческие причины моббинга.docx

• Противомикробные и противопаразитарные средства.docx

• Тема Вирусы Зоря Таисия дкд106.pptx