Файл: Лекция 1 Множества и операции над ними. Понятие множества.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Из рисунка видно, что А В составляет
В составляет
15 10 20 (15+20) – 25 =10 человек.
Тогда А состоит из 15 – 10 =5 членов,
Примеры решения задач
1. Прочтите записи и перечислите элементы каждого из множеств:
A = {x |x ∈ N,x < 5};
D = {x |x ∈ Z,−5< x ≤ 2};
E = {x |x ∈ Z,−3 ≤ x ≤ 2};
F = {x |x ∈ N,4 ≤ x < 8}
Решение.
А={1, 2, 3, 4}
D={-4, -3, -2, -1, 0, 1, 2}
E={-3, -2, -1, 0, 1, 2}
F={4,5,6,7}
2. Установите, какое из подмножеств А или В является подмножеством другого множества, если:
1) А={1; 2; 3; ... 10}, В={2; 4; 6 ;8};
2) А={2; 4; 6; 8; 10}, В - множество чисел первого десятка;
Решение.
1) В А;
А;
2) А В.
В.
3. Найдите пересечение множества А различных букв, входящих в слово “педагогика”, и множества В, букв, входящих в слово “математика”.
Найдите объединение множеств А и В.
Решение.
1) А∩В={а; е; и; к};
2) А В ={м; а; т; е; к; п; д; г; о}.
В ={м; а; т; е; к; п; д; г; о}.
4. Найти разности А\В и В\А множеств А и В, если:
1) A=[3; 5], B=[4; 8];
2) A={x|x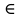 R, 1
R, 1
Решение.
1) А\В=[3; 4[ и В\А=]5; 8];
2) А\В=]1; 2[ и В\А=]4; 8].
5. Найти дополнение множества В до множества А, если В А:
А:
1) A={x|x R, -∞
2) A=[3; ∞), B=[5; 6].
Решение.
1) B =(-∞;1[и]2;5[;
2) B =[3;5[и] 6; ∞).
6. Найдите множества А и В, если:
AХB={(c; a), (c; y), (т; a), (т; y), (o; a), (o; y), (л; а), (л; у)}.
Решение.
А={c; т; o; л; };
В={a; y}.
Задачи для самостоятельного решения
1. Изобразите на числовой прямой множество:
x|x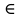 N, x
N, x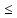 3
3
2. Изобразите на числовой прямой множество:
x|x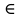 Z, - 2
Z, - 2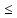 x
x 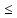 2
2
3. Изобразите на числовой прямой множество:
а) М= {х |x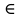
N , x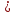 3} ; б) S={х |x
3} ; б) S={х |x  Z, -2
Z, -2
4. Изобразите на числовой прямой множество:
М={х |x N , x
N , x 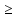 -7}
-7}
5. Найдите пересечение числового отрезка [-1; 7] с числовым
отрезком [7; 9].
6. Найдите объединение числового отрезка [-11; 0] с числовым
отрезком [3; +∞].
7. Из 25 учащихся класса 15 увлекаются математикой, а 12 –
русским языком. Каким может быть число учащихся,
увлекающихся обоими предметами? Увлекающихся хотя бы
одним предметом?
 В составляет
В составляет 15 10 20 (15+20) – 25 =10 человек.
Тогда А состоит из 15 – 10 =5 членов,
Примеры решения задач
1. Прочтите записи и перечислите элементы каждого из множеств:
A = {x |x ∈ N,x < 5};
D = {x |x ∈ Z,−5< x ≤ 2};
E = {x |x ∈ Z,−3 ≤ x ≤ 2};
F = {x |x ∈ N,4 ≤ x < 8}
Решение.
А={1, 2, 3, 4}
D={-4, -3, -2, -1, 0, 1, 2}
E={-3, -2, -1, 0, 1, 2}
F={4,5,6,7}
2. Установите, какое из подмножеств А или В является подмножеством другого множества, если:
1) А={1; 2; 3; ... 10}, В={2; 4; 6 ;8};
2) А={2; 4; 6; 8; 10}, В - множество чисел первого десятка;
Решение.
1) В
 А;
А;2) А
 В.
В.3. Найдите пересечение множества А различных букв, входящих в слово “педагогика”, и множества В, букв, входящих в слово “математика”.
Найдите объединение множеств А и В.
Решение.
1) А∩В={а; е; и; к};
2) А
 В ={м; а; т; е; к; п; д; г; о}.
В ={м; а; т; е; к; п; д; г; о}.4. Найти разности А\В и В\А множеств А и В, если:
1) A=[3; 5], B=[4; 8];
2) A={x|x
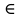 R, 1
R, 1Решение.
1) А\В=[3; 4[ и В\А=]5; 8];
2) А\В=]1; 2[ и В\А=]4; 8].
5. Найти дополнение множества В до множества А, если В
 А:
А:1) A={x|x R, -∞
2) A=[3; ∞), B=[5; 6].
Решение.
1) B =(-∞;1[и]2;5[;
2) B =[3;5[и] 6; ∞).
6. Найдите множества А и В, если:
AХB={(c; a), (c; y), (т; a), (т; y), (o; a), (o; y), (л; а), (л; у)}.
Решение.
А={c; т; o; л; };
В={a; y}.
Задачи для самостоятельного решения
1. Изобразите на числовой прямой множество:
x|x
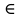 N, x
N, x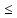 3
32. Изобразите на числовой прямой множество:
x|x
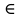 Z, - 2
Z, - 2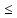 x
x 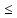 2
23. Изобразите на числовой прямой множество:
а) М= {х |x
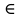
N , x
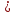 3} ; б) S={х |x
3} ; б) S={х |x  Z, -2
Z, -24. Изобразите на числовой прямой множество:
М={х |x
 N , x
N , x 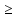 -7}
-7}5. Найдите пересечение числового отрезка [-1; 7] с числовым
отрезком [7; 9].
6. Найдите объединение числового отрезка [-11; 0] с числовым
отрезком [3; +∞].
7. Из 25 учащихся класса 15 увлекаются математикой, а 12 –
русским языком. Каким может быть число учащихся,
увлекающихся обоими предметами? Увлекающихся хотя бы
одним предметом?