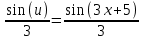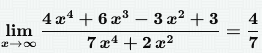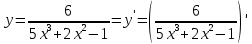Файл: Решение Неопределённость Домножаем на сопряжённое Сопряжённое для числителя.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 16
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Решение:
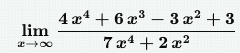Неопределённость ∞ - ∞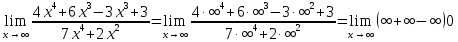
Делим числитель и знаменатель на
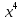
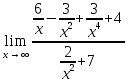
Сокращаем слагаемые
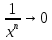при x 
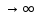
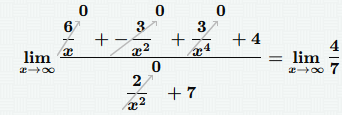
Предел от константы lim C = C
=
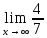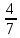
Н
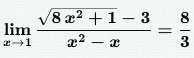айденный предел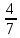 б)
Решение:
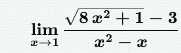Неопределённость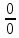 
=
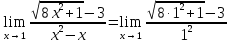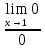
Домножаем на сопряжённое
Сопряжённое для числителя
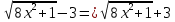
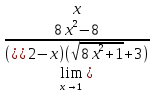
Разложение на множители
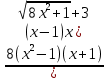
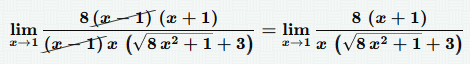
Подставляем значение x = 1 в функцию
и находим предел
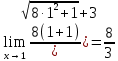
в)
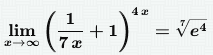
Решение:
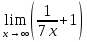
4x Неопределённость 1∞
4x = 
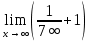4∞ =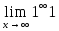 
Преобразование 4x = 7x
7x 
Второй замечательный предел
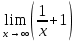x= e, где 
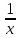→0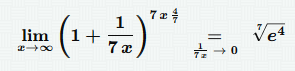
Найденный предел
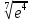
Постоянный множитель (cu)’= c·u’
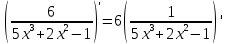
Деление
=
=
=
=
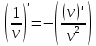
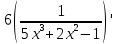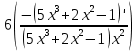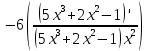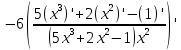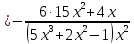Искомая производнаяб) y=cos(3x-sinx)
Заменим u=3x-sinx
Производная косинус есть минус синус cos(u)=-sin(u)
Дифференцируем 3x-sin(x) почленно:
-
3x Производная произведения константы на функцию есть произведение этой константы на производную данной функции. Применим x получим 1. Получим 3 -
- sin(x) Производная произведения константы на функцию есть произведение этой константы на производную данной функции. Производная синуса есть косинус. Получим –cos(x) -
В результате 3-cos(x) -
В результате последовательности правил –(3-cos(x))sin(3x-sin(x)) -
Упрощаем: (cos(x)-3)sin(3x-sin(x)
в)
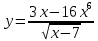
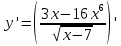
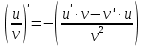
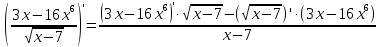
Линейность (au-bv)’=a·u’-b·v’ и сложная функция
=
=
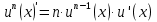
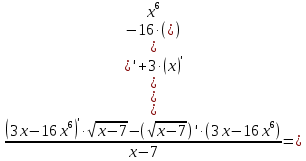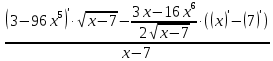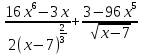
a)
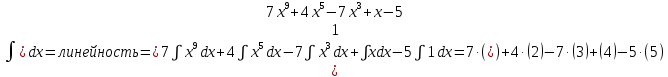
(1) Интеграл от степенной функции ʃ
=
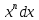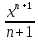при n=9ʃ
=
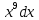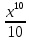
(2) Интеграл от степенной функции ʃ
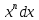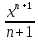= при n=5ʃ
=
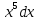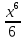
(3) Интеграл от степенной функции ʃ
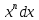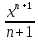= при n=3ʃ
=
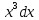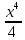
(4) Интеграл от степенной функции ʃ
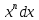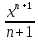= при n=1ʃ x
=
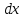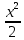
(5) ʃ
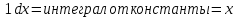
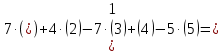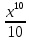7· +4·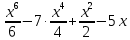
б) ʃ
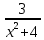
dx
Используем подстановку
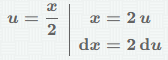
ʃ
dx = 3ʃ
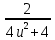duВыносим общий множитель и преобразовываем
3ʃ
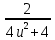du = 3ʃ
= 
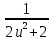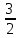·arctg(u) =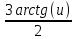 
Производим обратную замену
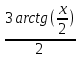
в) ʃcos(3x+5)dx
Используем подстановку
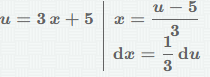
ʃcos(3x+5)dx = ʃ
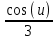du =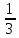 
·sin(u) =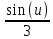 
Производим обратную замену
