ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 89
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Тамбовский государственный технический университет»

Институт заочного обучения
Кафедра "Материалы и технология"
Контрольная работа по предмету: «Кристаллография»
Вариант № 6
Выполнил: студент группы БМТ-211з
Власов Ю. Н.
Проверил: д.т.н., профессор
Мордасов Д. М.
Тамбов 2023
Задание 1. Линейные и угловые соотношения в пространственной решетке
1.1. Вычислить угол φ между кристаллографическими плоскостями (h1 k1 l1) и (h2 k2 l2) в кубическом кристалле и построить эти плоскости.
Дано:
(h1 k1 l1) = (1 2 3); (h2 k2 l2) = (3 2 0)
Решение:
cos φ =
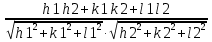 =
= 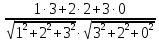 =
= =
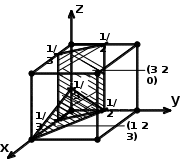 0, 518519
0, 518519φ = arccos (0, 518519) ≈ 59º
(h1 k1 l1) = (1 2 3) = 1;
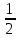 ;
; 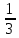
(h2 k2 l2) = (3 2 0) =
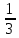 ;
; 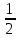 ; 0
; 0Ответ: φ ≈ 59º
1.2. Вычислить угол φ между кристаллографическими направлениями
[u1 v1 w1] и [u2 v2 w2] в кубическом кристалле и построить эти направления.
Дано:
[u1 v1 w1] = [2 1 3]; [u2 v2 w2] = [3 0 2]
Решение:
cos φ =
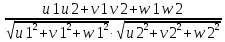 =
= 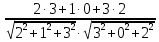 =
= = 0, 888889
φ = arccos (0, 888889) ≈ 27
Поделим на наибольшее число, чтобы поместить в единичную кубическую решетку
[
 u1 v1 w1] = [2 1 3] = [
u1 v1 w1] = [2 1 3] = [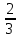
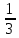 1]
1][u2 v2 w2] = [3 0 2] = [1 0
 ]
]Ответ: φ ≈ 27º
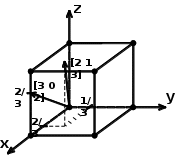
1.3. Определить принадлежность направления с индексами [uvw] плоскости (hkl) в кубическом кристалле и построить плоскость и направление.
Дано:
[u v w] = [
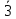 0 2]; (h k l) = (2 1 3)
0 2]; (h k l) = (2 1 3)Решение:
Условием принадлежности является равенство 0.
uh + vk + wl = 0
-
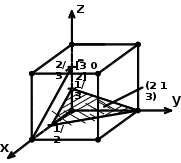 3·2 + 0·1 + 2·3 = 0
3·2 + 0·1 + 2·3 = 0Равенство нулю выполняется, следовательно, направление принадлежит плоскости.
(h k l) = (2 1 3) =
 ; 1;
; 1; 
[u v w] = [
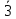 0 2] = [
0 2] = [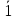 0
0  ]
] Ответ: Направление принадлежит плоскости
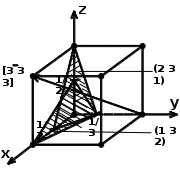
1.4. Найти индексы [u v w] линии пересечения двух плоскостей (h1 k1 l1) и (h2 k2 l2) в кубическом кристалле. Построить плоскости, указать линию их пересечения.
Дано:
(h1 k1 l1) = (2 3 1); (h2 k2 l2) = (1 3 2)
Решение:
Составим систему уравнений, неизвестные индексы которых и будут индексами линии пересечения плоскостей:
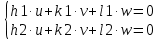
Δ
 =
= 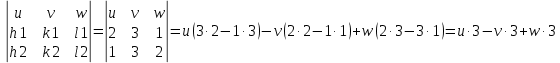
[u v w] = [3
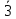 3]
3](h1 k1 l1) = (2 3 1) =
 ;
;  ; 1
; 1(h2 k2 l2) = (1 3 2) = 1;
 ;
; 
[u v w] = = [3
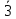 3] = [1
3] = [1 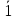
1]
Ответ: [u v w] = [3
 3]
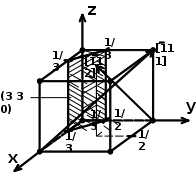
3]1.5. Найти индексы плоскости в кубическом кристалле, в которой лежат направления [u1v1w1] и [u2v2w2]. Проверить расчет построением направлений и плоскости в кубической ячейке.
Дано:
[u1v1w1] = [
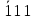 ]; [u2v2w2] = [
]; [u2v2w2] = [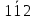 ]
]Решение:
Составим систему уравнений, неизвестные индексы которых и будут индексами плоскости.
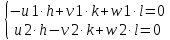
Δ
 =
= 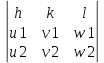 =
= 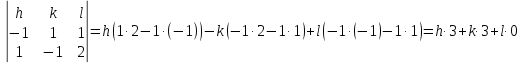
(h k l) = (3
 0)
0) [u1v1w1] = [
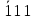 ]
] [u2v2w2] = [
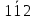 ] = [
] = [ 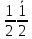 1]
1](h k l) = (3
 0) =
0) =  ;
;
 ; 0
; 0Ответ: (h k l) = (3 3 0)
Задание 2. Симметрические преобразования в кристаллах
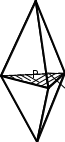
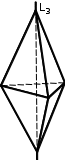
Задание: Определить вид симметрии кристалла - тригональная дипирамидаи изобразить графически элементы симметрии.
Тригональная дипирамида относится средней категории тригональной сингонии, т.е. в ней есть ось симметрии третьего порядка, единичное направление одно и совпадает с осью. Форму дипирамиды можно рассматривать как две пирамиды, сложенные основаниями. Вершины двух пирамид лежат на одной оси симметрии и при повороте на 120° кристалл самосовмещается. Нижние грани находятся точно под верхними и связаны с ними плоскостью симметрии, совпадающей с плоскостью общего основания. Центр симметрии отсутствует.
Таким образом, вид симметрии тригональной дипирамиды: L3P