Файл: Варианты ответов 1.doc

Скачать файл (1,18Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 26.10.2023

Просмотров: 484

Скачиваний: 18

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

№	Вопросы	Варианты ответов
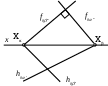
67.	Проекции перпендикуляра к плоскости располагаются следующим образом:	1) горизонтальная проекция перпендикуляра перпендикулярна проекции прямой, находящейся в плоскости, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции этой прямой 2) горизонтальная проекция перпендикуляра проходит через горизонтальный след прямой, лежащей в плоскости, а фронтальная проекция перпендикуляра проходит через фронтальный след этой прямой 3) проекции перпендикуляра перпендикулярны проекциям любой прямой, лежащей в этой плоскости 4) проекции перпендикуляра перпендикулярны проекциям прямых частного положения, лежащим в этой плоскости 5) горизонтальная проекция перпендикуляра перпендикулярна горизонтальному следу плоскости, а фронтальная проекция перпендикуляра перпендикулярна фронтальному следу плоскости
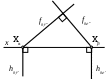
68.	Если фронтальные следы плоскостей  и  взаимно перпендикулярны, то эти плоскости	1) также взаимно перпендикулярны 2) пересекаются 3) параллельны 4) перпендикулярны плоскости ₂ 5) занимают частное положение по отношению к плоскостям проекций
69.	Если фронтальные следы плоскостей  и  взаимно перпендикулярны, то эти плоскости	1) также взаимно перпендикулярны 2) пересекаются 3) параллельны 4) перпендикулярны плоскости ₁ 5) проходят через одну из осей проекций

№	Вопросы	Варианты ответов
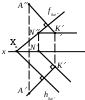
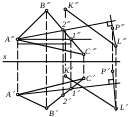
70.	Прямая АК	1) перпендикулярна плоскости ₂ 2) перпендикулярна плоскости ₁ 3) параллельна плоскости  4) перпендикулярна плоскости  5) занимает произвольное положение относительно плоскости 
71.	Плоскости  и 	1) взаимно перпендикулярны 2) перпендикулярны прямой КМ₂ 3) взаимно параллельны 4) перпендикулярны плоскости ₁ 5) невозможно установить их взаимное положение
72.	Две плоскости являются взаимно перпендикулярными, если	1) одна из плоскостей проходит через прямую, перпендикулярную другой плоскости 2) они содержат взаимно перпендикулярные прямые 3) их следы также взаимно перпендикулярны 4) хотя бы одна пара одноименных следов этих плоскостей перпендикулярна друг другу 5) обе плоскости перпендикулярны третьей плоскости
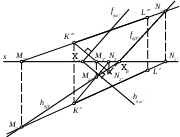
73.	Плоскость, заданная двумя пересекающимися прямыми KL и PL	1) перпендикулярна плоскости  АВС 2) перпендикулярна прямой А2 3) параллельна плоскости  АВС 4) перпендикулярна плоскости ₁ 5) занимает произвольное положение относительно плоскости  АВС

№	Вопросы	Варианты ответов
74.	Способ вращения заключается	1) во введении одной или нескольких дополнительных плоскостей проекций при неизменном положении геометрического элемента 2) в изменении положения в пространстве геометрического элемента путем его вращения вокруг оси проекций 3) в изменении положения в пространстве геометрического элемента путем его вращения вокруг некоторой неподвижной оси при неизменном положении плоскостей проекций 4) в приведении геометрических элементов, расположенных в общем положении, в частное 5) в последовательном вращении геометрических элементов вокруг некоторой неподвижной оси вместе с плоскостями проекций
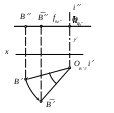
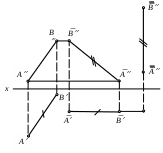
75.	Точка В	1) вращается вокруг оси i, перпендикулярной плоскости ₂ 2) вращается вокруг оси i, перпендикулярной плоскости ₁ 3) вращается вокруг оси i, параллельной плоскости ₁ 4) вращается вокруг оси i, параллельной плоскости ₂ 5) вращается вокруг оси проекций x
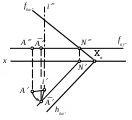
76.	Определите действия, совершенные с точкой А.	1) Вращением вокруг оси i, перпендикулярной плоскости ₁, точка А совмещена с плоскостью . 2) Вращением вокруг оси i, перпендикулярной плоскости ₁, точка А совмещена с плоскостью проекций ₂. 3) Вращением вокруг оси i, перпендикулярной плоскости ₁, точка А совмещена с плоскостью . 4) Вращением вокруг оси i, параллельной плоскости ₁, точка А совмещена с плоскостью . 5) Вращением вокруг оси i, перпендикулярной плоскости ₂, точка А совмещена с плоскостью .

№	Вопросы	Варианты ответов
77.	При вращении точки вокруг некоторой неподвижной прямой она перемещается	1) по прямой, параллельной оси x 2) по дуге окружности, находящейся в плоскости проекций 3) в плоскости, параллельной оси вращения 4) по прямой, перпендикулярной оси вращения 5) в плоскости, перпендикулярной оси вращения
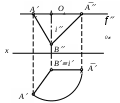
78.	Положение отрезка АВ преобразовано	1) в положение, параллельное плоскости ₂ 2) в положение, параллельное плоскости ₁ 3) в положение, перпендикулярное плоскости ₂ 4) в положение, перпендикулярное плоскости ₁ 5) в произвольное положение
79.	При вращении точек, расположенных на оси вращения, считается, что	1) они вращаются вместе с осью проекций 2) они не изменяют своего положения 3) они перемещаются по оси вращения 4) они вращаются вокруг другой неподвижной оси 5) невозможно преобразовать их положение
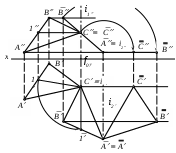
80.	Для построения треугольника , истинной величины треугольника АВС, первоначальное положение изменялось путем вращения вокруг осей:	1) i₁₁, i₂₂ 2) i₁  ₂, i₂  ₁ 3) i₁  ₁, i₂  ₂ 4) i₁  ₂, i₂  ₁ 5) i₁  ₁, i₂  ₂

№	Вопросы	Варианты ответов
81.	Поворот вокруг оси, перпендикулярной плоскости проекций без указания на чертеже осей вращения называется	1) вращением вокруг горизонтали 2) переменой плоскостей проекций 3) параллельным переносом 4) методом совмещения 5) плоскопараллельным перемещением
82.	Определите действия, проведенные с отрезком АВ.	1) Методом плоскопараллельного перемещения отрезок АВ преобразован в положение, перпендикулярное плоскости ₁. 2) Методом совмещения отрезок АВ преобразован в положение, перпендикулярное плоскости ₁. 3) Методом вращения вокруг горизонтали отрезок АВ преобразован в положение, перпендикулярное плоскости ₁. 4) Методом плоскопараллельного перемещения отрезок АВ преобразован в положение, параллельное плоскости ₁. 5) Методом вращения отрезок АВ преобразован в произвольное положение.
83.	Можно ли способом вращения определить угол наклона прямой к плоскости ₁?	1) Да, если прямая вращается вокруг оси, перпендикулярной плоскости ₂, до положения, параллельного ₁. 2) Да, если прямая вращается до совмещения с плоскостью ₁. 3) Да, если прямая вращается вокруг оси, перпендикулярной плоскости ₁, до положения, параллельного ₂. 4) Да, если это прямая частного положения. 5) Нет, невозможно.
84.	Плоскость вращения точки, если ось вращения является горизонталью, является плоскостью	1) общего положения 2) фронтально-проецирующей 3) горизонтальной 4) фронтальной 5) горизонтально-проецирующей