ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 486
Скачиваний: 18
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| № | Вопросы | Варианты ответов |
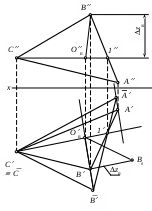
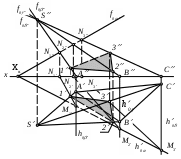
| Методом вращения вокруг горизонтали C1 определена истинная величина треугольника АВС. Истинная величина радиуса вращения точки В равна | 1) отрезку ВОВ 2) отрезку ВОВ 3) отрезку ВВ0 4) отрезку ОВВ0 5) zB |
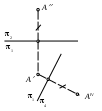
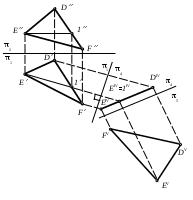
| На рисунке определена истинная ве личина угла между прямой LT и плоскостью . Это угол | 1) 1 2) 2 3) 3 4) 4 5) 5 |
| № | Вопросы | Варианты ответов |
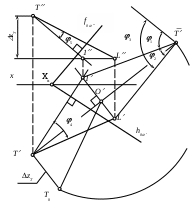
| На рисунке определена истинная величина угла между плоскостью и плоскостью треугольника АВС. Это угол | 1) 1 2) 2 3) 3 4) 4 5) 5 |
88. | Вращение плоскости вокруг ее следа до совмещения с соответствующей плоскостью проекций называется | 1) способом вращения вокруг оси, параллельной плоскости проекций 2) способом вращения вокруг оси, перпендикулярной плоскости проекций 3) способом перемены плоскостей проекций 4) способом совмещения 5) плоскопараллельным перемещением |
| Д 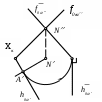 ля того, чтобы произвольно расположенную плоскость перевести во фронтально-проецирующую, за ось вращения следует принять прямую, ля того, чтобы произвольно расположенную плоскость перевести во фронтально-проецирующую, за ось вращения следует принять прямую,  | 1) перпендикулярную плоскости проекций 3 2) перпендикулярную плоскости проекций 2 3) перпендикулярную плоскости проекций 1 4) параллельную плоскости проекций 1 5) параллельную плоскости проекций 2 |
| № | Вопросы | Варианты ответов |
| Точка А, принадлежащая плоскости , совмещена с горизонтальной плоскостью проекций. ПрямаяАА является | 1) горизонтальной проекцией горизонтали, проходящей через точку А 2) горизонтальным следом плоскости вращения точки А 3) перпендикуляром, опущенным из точки А к плоскости 4) осью вращения точки А 5) линией проекционной связи |
91. | Метод перемены плоскостей проекций заключается | 1) во введении одной или нескольких дополнительных плоскостей проекций при неизменном положении геометрического элемента 2) в изменении положения в пространстве геометрического элемента путем его вращения вокруг оси проекций 3) в изменении положения в пространстве геометрического элемента путем его вращения вокруг некоторой неподвижной оси при неизменном положении плоскостей проекций 4) в приведении геометрических элементов, расположенных в общем положении, в частное 5) в последовательном вращении геометрических элементов вокруг некоторой неподвижной оси вместе с плоскостями проекций |
| Точка АIV – проекция точки А на плоскости 4. Прямая ААIV является | 1) горизонтальной проекцией горизонтали, проходящей через точку А 2) горизонтальным следом плоскости вращения точки А 3) перпендикуляром, опущенным из точки А к плоскости 4) осью вращения точки А 5) линией проекционной связи |
| № | Вопросы | Варианты ответов |
93. | Какому обязательному условию должна отвечать плоскость 4, вводимая в качестве дополнительной плоскости проекций в систему плоскостей 1 и 2? | 1) 4 1 и 4 2 2) 4 1 3) 4 1 или 4 2 4) 4 2 5) 4 1 или 4 2 |
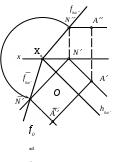
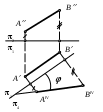
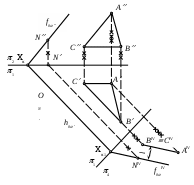
| Проекция АIVBIV является натуральной величиной отрезка АВ, а угол – | 1) углом наклона прямой АВ к плоскости проекций 2 2) углом между прямой АВ и осью х 3) углом наклона прямой АВ к плоскости проекций 1 4) углом наклона прямой АВ к плоскости проекций 4 5) углом межу проекциями АВ и АIVBIV |
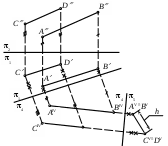
| Отрезок KIVDIV определяет | 1) истинную величину расстояния от точки К до плоскости проекций 1 2) истинную величину расстояния от точки К до плоскости проекций 2 3) истинную величину расстояния от точки К до прямой АС 4) истинную величину расстояния от точки К до плоскости треугольника АВС 5) истинную величину расстояния от точки К до прямой ВС |
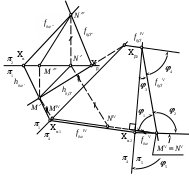
| Расстояние h выражает истинную величину расстояния | 1) между двумя скрещивающимися прямыми АВ и CD 2) между двумя параллельными прямыми АВ и CD 3) между прямой АВ и плоскостью проекций 2 4) между прямой CD и плоскостью проекций 2 5) между прямой АВ и плоскостью, проходящей через прямую CD |
| № | Вопросы | Варианты ответов |
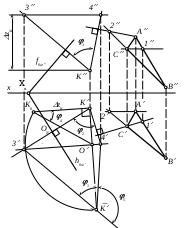
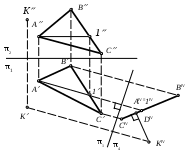
| Для нахождения истинной величины треугольника АВС методом перемены плоскостей проекций введены две дополнительные плоскости 4 и 5 по следующей схеме: | 1) 4 2 и 4 (Е1); 5 2 и 5 ( АВС) 2) 4 1 и 4 (Е1); 5 4 и 5 ( АВС) 3) 4 1 и 4 (Е1); 5 4 и 5 ( АВС) 4) 4 1 и 4 (Е1); 5 4 и 5 ( АВС) 5) 4 1 и 5 1 |
| Расстояние l выражает истинную величину расстояния | 1) между двумя параллельными плоскостями – плоскостью и плоскостью треугольника АВС 2) между двумя скрещивающимися плоскостями – плоскостью и плоскостью треугольника АВС 3) между двумя параллельными прямыми f0IV и BC 4) между прямой АВ и плоскостью 5) между плоскостью и плоскостью проекций 1 |
| № | Вопросы | Варианты ответов |
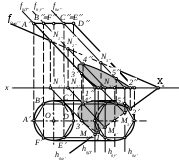
| Истинной величиной угла между плоскостями и является угол | 1) 1 2) 2 3) 3 4) 4 5) 5 |
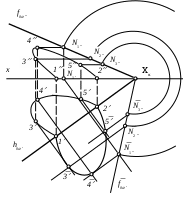
| Истинная величина части эллипса 1-3-4-5-2 найдена | 1) способом вращения вокруг оси, перпендикулярной плоскости проекций 2) методом перемены плоскостей проекций 3) способом совмещения 4) способом вращения вокруг горизонтали 5) способом плоскопараллельного перемещения |
| № | Вопросы | Варианты ответов |
| Для построения сечения пирамиды SABC плоскостью использован | 1) способ «граней», т.е. найдены линии пересечения граней пирамиды с плоскостью 2) способ «ребер», т.е. найдены точки встречи ребер пирамиды с плоскостью 3) метод нормального сечения, т.е. пирамида рассечена вспомогательной плоскостью, перпендикулярной ее ребрам 4) способ треугольников 5) метод раскатки |
102. | В общем случае, построение сечения линейчатой поверхности (конуса или цилиндра) проводится путем | 1) аппроксимации ее поверхности многогранной (пирамидальной или призматической) 2) проведения вспомогательных секущих плоскостей 3) замены данных плоскостей проекций на плоскости, по отношению к которым линейчатая поверхность будет занимать некоторое частное положение 4) совмещения ее поверхности с плоскостью проекций 5) преобразования проекций |
| В направлении на плоскость 2 невидимой частью сечения поверхности цилиндра плоскостью будет кривая | 1) 1-3 2) 1-3-4-5-2 3) 3-4-5-2 4) 4-5-2 5) 5-2 |
| № | Вопросы | Варианты ответов |
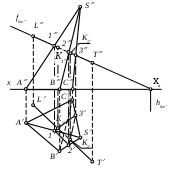
| Определите правильный алгоритм нахождения точек пересечения К1 и К2 прямой LT с поверхностью пирамиды SABC. | 1) Через прямую проведена вспомогательная фронтально-проецирующая плоскость , построено сечение 123 этой вспомогательной плоскостью и найдены искомые точки в пересечении прямой LT с контурами построенного сечения. 2) Через ребра пирамиды проведены вспомогательные плоскости, построено сечение 123 и найдены искомые точки в пересечении прямой LT с контурами построенного сечения. 3) Построена линия пересечения плоскости с пирамидой SABC, в плоскости выбрана произвольная прямой LT и найдены искомые точки в пересечении прямой LT с построенной линией пересечения. 4) Определены грани, в которых прямая LT пересекает поверхность пирамиды SABC и построены точки пересечения прямой LT с этими гранями. 5) В гранях пирамиды SABC построены вспомогательные прямые 12, 23 и 34 и найдены точки пересечения этих прямых с заданной прямой LT. |
105. | В чем заключается общность способов построения точек пересечения прямой линии с поверхностью многогранника и прямой линии с плоскостью. | 1) Применяется один из способов преобразования проекций. 2) Через прямую и ребра пирамиды проводится вспомогательная секущая плоскость частного положения. 3) Применяется способ вспомогательных секущих плоскостей, проходящих через ребра многогранника. 4) Вводится дополнительная плоскость проекций, перпендикулярная плоскости 1 или 2. 5) Через прямую проводится вспомогательная плоскость (частного положения) и строится фигура, образуемая в пересечении этой плоскости с заданным геометрическим элементом. |