Лабораторная работа № 3Определение моментов инерции телс помощью трифилярного подвесаи проверка теоремы ШтейнераЦель работы

1. 
   Определение моментов инерции некоторых тел методом крутильных колебаний с помощью трифиллярного подвеса;
   
2. 
   Проверка теоремы Штейнера.
   

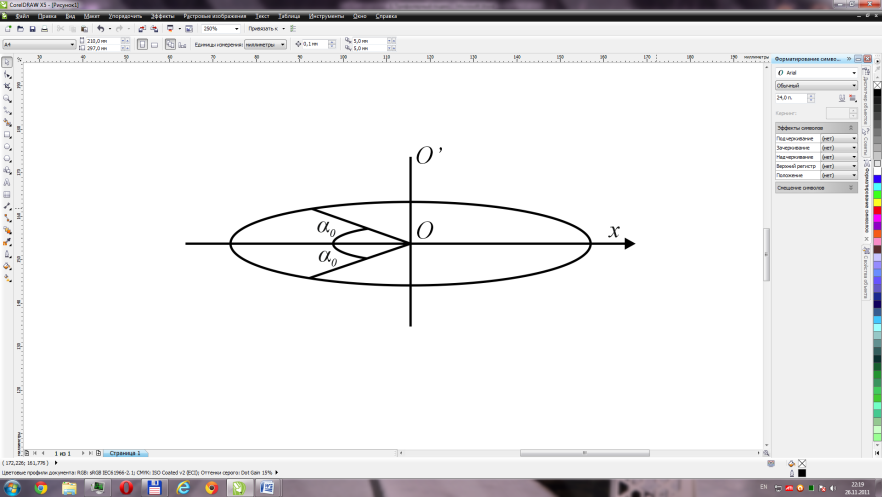
Приборы и принадлежности Трифиллярный подвес, секундомер, линейка, штангенциркуль, исследуемые тела (два диска-груза).Краткая теорияОдним из методов измерения моментов инерции твердых тел является метод трифиллярного подвеса, совершающего крутильные колебания.Поэтому, вначале определим, какие колебания называются крутильными, затем ознакомимся с устройством трифиллярного подвеса.Рис. 1. Крутильные колебанияГармоническими крутильными колебаниями тела называются периодические движения относительно оси, проходящей через центр масс этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса (рис. 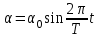1):(1)где 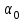– амплитуда колебаний; 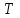– период колебаний.Устройство трифиллярного подвесаТрифиллярный подвес состоит из подвижного диска платформы Р (в дальнейшем просто платформа) массой

---

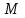
, радиуса 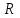, подвешенного на трех симметрично расположенных нитях (рис 2.a). Наверху эти нити симметрично закреплены по краям диска Р' меньшего радиуса .

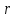При повороте верхнего диска P' на небольшой угол вокруг вертикальной оси OO' все три нити принимают наклонное положение. Центр тяжести системы несколько приподнимается по оси вращения OO' (рис. 2.b).



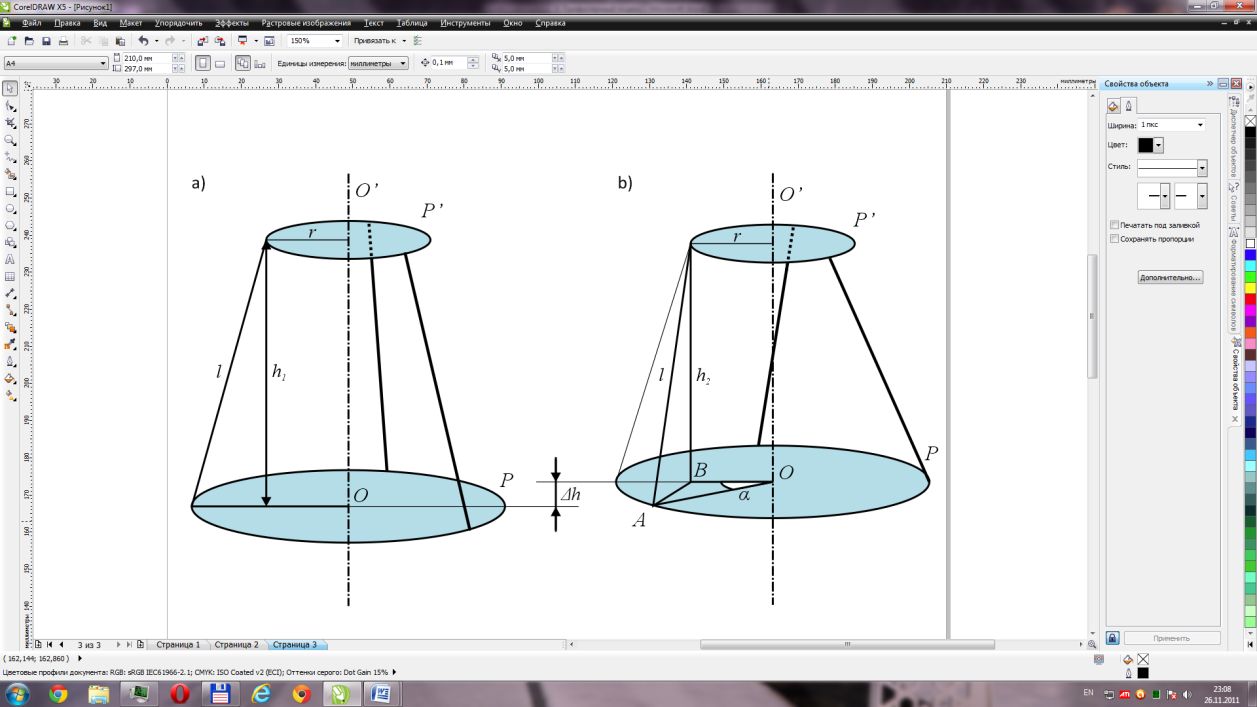
Рис. 2. Трифилярный подвес

Период крутильных колебаний и момент инерции плат­формы

Пусть при вращении платформа поднимется на высоту 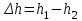, тогда приращение ее потенциальной энергии равно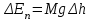



где 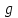– ускорение свободного падения.

При вращении платформы в обратную сторону потенциальная энергия переходит в кинетическую энергию вращательного движения

,

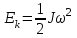где 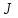– момент инерции платформы;

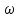– ее угловая скорость.

В момент прохождения положения равновесия кинетическая энергия максимальна. Если пренебречь трением, то на основании закона сохранения энергии можно записать для колеблющейся платформы

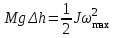(2)

Угловую скорость платформы можно найти, взяв производную по времени от (см. (1))



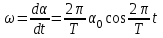
Очевидно, что

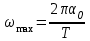(3)

Найдем величину 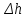при поворотах платформы на угол ₀, считая, что 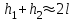( 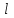– длина нити)

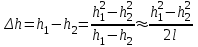(4)

Из рис. 2 а, b

---

видно, что



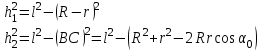
Подставляя значения 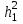и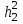 в формулу (4) получим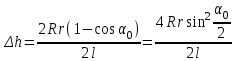



Ввиду малости угла ₀ синус заменим аргументом

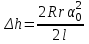(5)

Подставляя выражения (3) и (5) в формулу (2), получим окончательно

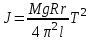(6)

Поскольку параметры прибора , , во время опыта не меняются, формулу (6) удобно применять в виде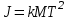

(7)

где

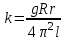
Аддитивность моментов инерции

Аддитивность (лат. additivus – прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям.

Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей. Примеры аддитивных величин: энергия, импульс, энтропия, мощность, давление, электрический заряд.

Общий момент инерции нескольких тел равен сумме моментов инерции отдельных тел, если центр масс каждого из них лежит на оси вращения.

Если на платформу поместить некоторое тело массой 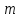, так, чтобы равномерное натяжение нитей не нарушалось, то момент инерции этой системы находят по формуле (6) или (7), где вместо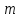 будет сумма масс  .

---

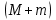А так как момент инерции величина аддитивная, т.е. 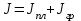, то можно определить момент инерции исследуемого тела: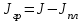



где 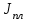, 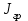– момент инерции платформы и груза.

Теорема Штейнера

Момент инерции тела относительно произвольной оси AA’ равен сумме момента инерции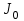 тела относительно оси BB’, параллельной данной и проходящей через центр масс тела С, и произведения массы тела на квадрат расстояния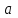 между осями (рис. 3)

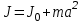(8)

В соответствии с теоремой Штейнера момент инерции диска относительно оси AA’, равен моменту инерции относительно оси BB’, проходящей через центр масс, 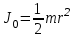плюс

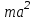
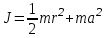(9)

Таким образом, с удалением центра масс тела от оси вращения его момент инерции относительно этой оси возрастает. Момент инерции системы тел зависит не только от его массы, но и от распределения масс в системе относительно оси вращения.



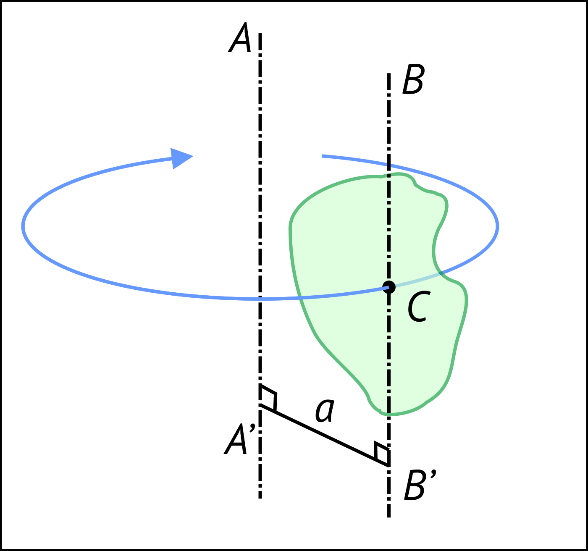
Рис. 3. Теорема Штейнера

Ход работы

1. 
   Определение момента инерции ненагруженной платформы
   
   1. 
      Поворотом на небольшой угол 3°–5° верхнего диска сообщить платформе колебательное движение. Измерить время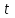 для N₁полных колебаний и вычислить период одного колебания:
      

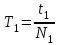
где 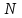– число полных колебаний.Таблица 1.1

№	N1	t1, c	T1, c
1	10
2	10
3	10
Среднее значение

---

2. 
   Определив величины , , , , определить теоретическое значение момента инерции платформы по формуле для сплошного однородного диска (цилиндра), а также экспериментальное значение:
   

Таблица 1.2

Экспериментальное значение момента инерции платформы	Теоретическое значение момента инерции платформы

3. 
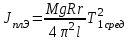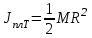   Сравнить с экспериментальное значение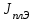 с теоретическим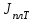
   
1. 
   Определение момента инерции исследуемого тела
   
   1. 
      Расположить два груза, имеющих форму диска, на платформе так, чтобы центр масс каждого из них лежал на оси вращения системы (в центре платформы).
      
   2. 
      Повторить измерения п.1.1. и определить период колебаний .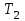
      

Таблица 2.1

№	N2	t2, c	T2, c
1	10
2	15
3	20
Среднее значение

3. 
   Определить момент инерции платформы с грузами в центре по формуле (6):
   

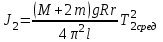,где – масса одного груза.

---

Смотрите также файлы

• Бекітемін 7 жббм директоры А. Ш. Абдишева 2023 ж.docx

• Модель жизненного цикла организации Л. Грейнера.ppt

• Анализ расчетов с поставщиками и покупателями в ооо Агрос Кстовского муниципального округа Нижегородской области.docx

• Выпускная квалификационная работа посвящена теме Разработка кадрового документооборота при найме персонала в организации.docx

• Программа для работы с электронными таблицами от Microsoft, входящая в группу продуктов Office для бизнесприложений. Microsoft Excel позволяет пользователям форматировать, упорядочивать и вычислять данные в электронной таблице.docx