Файл: Программа для работы с электронными таблицами от Microsoft, входящая в группу продуктов Office для бизнесприложений. Microsoft Excel позволяет пользователям форматировать, упорядочивать и вычислять данные в электронной таблице.docx

Решение задач линейной алгебры с помощью пакета Ms Excel

Оглавление

Введение

Excel — это программа для работы с электронными таблицами от Microsoft, входящая в группу продуктов Office для бизнес-приложений. Microsoft Excel позволяет пользователям форматировать, упорядочивать и вычислять данные в электронной таблице.

Организуя данные с помощью программного обеспечения, такого как Excel, аналитики данных и другие пользователи могут упростить просмотр информации по мере добавления или изменения данных. Excel содержит большое количество полей, называемых ячейками, которые упорядочены по строкам и столбцам. В эти ячейки помещаются данные.  

Excel является частью пакетов Microsoft Office и Office 365 и совместим с другими приложениями пакета Office. Программное обеспечение для работы с электронными таблицами доступно для платформ Windows, macOS, Android и iOS.

Microsoft Excel: линейная алгебра

Microsoft Excel — программа для работы с электронными таблицами, разработанная компанией Microsoft и входящая в состав программных продуктов. Электронная таблица представляет собой сетку, в которой данные и расчеты организованы в столбцы и строки. Пересечение столбца и строки называется ячейкой. Электронная таблица позволяет пользователям хранить, упорядочивать, обрабатывать и анализировать данные в ячейках электронной таблицы. На момент публикации это программное обеспечение находится в версии 2016 года.

Excel чаще всего используется в бизнес-настройках. Например, он используется в бизнес-анализе, управлении человеческими ресурсами , управлении операциями и составлении отчетов об эффективности. Excel использует большую коллекцию ячеек, отформатированных для организации данных и управления ими, а также для решения математических функций. Пользователи могут упорядочивать данные в электронной таблице, используя графические инструменты, сводные таблицы и формулы. Приложение для работы с электронными таблицами также имеет язык программирования макросов под названием Visual Basic для приложений [1].

Microsoft Excel широко и все чаще используется в качестве инструмента, помогающего инженерам проводить и воспроизводить сложные вычисления и анализ, проектировать сложные системы и управлять большими наборами данных. В этом курсе представлены некоторые темы инженерного анализа и способы их формулирования, реализации и решения в Microsoft Excel.

---

Этот курс представляет фундаментальные принципы и инженерные приложения задач линейной алгебры, а также демонстрирует инструменты, методы и стратегии Excel, которые можно использовать для их формулирования и решения [4].

Система линейных уравнений

Определение 1 : Набор из n линейных уравнений.



в k неизвестных x _j  можно рассматривать как матричное уравнение AX = C , где A — матрица размера n  ×  k [ a _ij ], X —  вектор-столбец размера k × 1 [ x _j ], а C —  вектор-столбец размера n × 1 [ с _j ].

Свойство 1 : Если A — квадратная матрица (т. е. количество уравнений равно количеству неизвестных), уравнение AX = C имеет единственное решение тогда и только тогда, когда A обратимо (т. е. det A ≠ 0), и в в этом случае единственное решение дается выражением X = A ^-1 C.

Свойство 2  ( правило Крамера ): если квадратная матрица A обратима, единственное решение AX = C определяется выражением



где A _j  - это A  с j -м столбцом, замененным элементами C .

Пример 1 : Решите следующую линейную систему, используя правило Крамера:



На рисунке 2 мы вычисляем det A  и det A _j  для каждого j .

Рисунок 1 – Вычисление определителя по правилу Крамера

Отсюда следует, что x  = -6/9 = -2/3, y = 3/9 = 1/3 и z  = 0/9 = 0.

В соответствии со свойством 1 мы можем получить тот же результат, вычислив A ^-1 C , что можно выполнить в Excel, используя формулу =ММНОЖ(МИНВЕРС( A ), C ). Для примера 1 это дает



Определение 2 [3]: Когда C из определения 1 не является нулевой матрицей, то линейные уравнения называются гетерогенными . При С = О  линейные уравнения называются 

---

однородными . В этом случае О  есть решение уравнения АХ = О , называемое тривиальным решением .

Свойство 3 : Если A  обратимо, то X = Ο  — единственное решение AX = Ο .

Доказательство . Это следует из свойства 1.

Наблюдение : когда А  необратимо (т. е. det А  = 0), любое скалярное число, кратное нетривиальному решению однородного уравнения АХ = О , также является решением. Чтобы найти такое решение, мы можем использовать метод исключения Гаусса, метод, аналогичный тому, который мы использовали для вычисления определителя квадратной матрицы на основе свойства 5 определителей и линейных уравнений . Этот подход работает для любого A  (квадратного или нет, обратимого или нет).

Определение 3 : Если A  — матрица размера n  ×  k , а B  — матрица размера n  ×  m , то расширенная матрица  A | B — матрица размера n  × ( k + m ), первые k столбцов которой идентичны столбцам  матрицы A  , а оставшиеся m  столбцов идентичны столбцам матрицы B.

Свойство 4 : Если A' и C' получены из A и C на основе любого из следующих преобразований, то уравнения AX = C  и A'X = C'  имеют одинаковые решения.

1. 
   Перестановка любых двух строк
   
2. 
   Умножение любой строки на константу
   
3. 
   Добавление любой строки, умноженной на константу, к другой строке
   

Наблюдение : Обычно мы применяем приведенные выше преобразования к расширенной матрице A | С .

Определение 4. Метод исключения Гаусса — это способ решения линейных уравнений, основанный на преобразованиях, описанных в свойстве 9. Предположим, что A  и C такие, как описано в определении 1.

         Шаг 0 – установить i  = 1 и j  = 1

Теперь мы применяем следующую серию преобразований к расширенной матрице (шаг 1 - шаг p  , где p  меньшее из n  и k ):

Шаг i _–  часть 1: Найдите r ≥  i такое, чтобы абсолютное значение rj  было наибольшим. Если a _rj  ≈ 0 (т. е. | a _rj | < ϵ, где ϵ — некоторое предопределенное малое значение), то при j = n процедура завершается; в противном случае замените j на j + 1 и повторите шаг i. Если не a _rj  ≈ 0 и 

---

r > k , то поменять местами строки r и i (правило 1).

Шаг i – _часть  2: Разделите все записи в строке i  на ij  (правило 2).

Шаг i _—  часть 3: Для каждой строки r ниже строки i добавьте — rj  , умноженное на строку i, до строки r (правило 3). Это гарантирует, что a _rc  = 0 для всех r > i и c ≤ j .

Наблюдение : Для неоднородных уравнений (т.е. C  ≠  Ο ) есть три возможности: существует бесконечное число решений, нет решений или есть единственное решение. Для однородных уравнений (т. е. С = О ) возможны две возможности: существует бесконечное число решений или существует единственное решение, а именно тривиальное решение, где X = О.

Пример 2. Решите следующую линейную систему с помощью исключения Гаусса:



На рис. 2 показаны этапы процесса исключения Гаусса для примера 2.

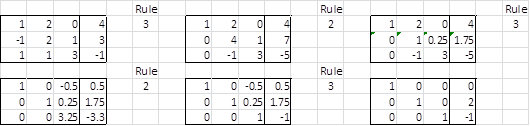Рисунок 2 – Решение линейных уравнений методом исключения Гаусса

Поскольку A преобразуется в единичную матрицу, мы знаем, что преобразование C является единственным решением системы линейных уравнений, а именно x = 0, y = 2 и z = -1. Обратите внимание, что мы получаем тот же результат, вычисляя X = A ^-1  C .

Пример 3. Решите следующую однородную линейную систему с помощью исключения Гаусса:



Путем исключения Гаусса из рисунка 3 мы видим, что единственным решением является тривиальное решение:

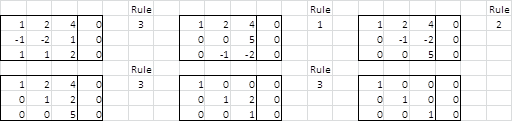Рисунок 3 – Решение однородного линейного уравнения

Пример 4. Решите следующую однородную линейную систему с помощью исключения Гаусса:



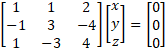
На этот раз метод исключения Гаусса создает строку со всеми нулями (см. рис. 4), а число ненулевых строк = 2 < 3 неизвестных. Таким образом, существует бесконечное множество решений.

---

Рисунок 4 – Поиск решений однородных линейных уравнений

Решения могут принимать вид x = -2,5 t , y = 0,5 t , z = t для любого значения t .

Наблюдение : Как видно из приведенных выше примеров, однородное уравнение AX = O , где A — матрица размера m  ×  n , имеет единственное решение, когда после выполнения исключения Гаусса остается n ненулевых строк. В противном случае уравнение имеет бесконечное число решений.

Реальные статистические функции Excel : Для выполнения процедуры исключения Гаусса предусмотрены следующие функции массива.

ELIM (R1, prec ): функция массива, которая выводит результаты исключения Гаусса для расширенной матрицы, найденной в массиве R1. Форма выхода такая же, как форма R1.

LINEQU (R1, prec ): функция массива, которая возвращает вектор-столбец n  × 1 с уникальным решением уравнений, определяемых расширенной матрицей m  × ( n +1), найденной в массиве R1; возвращает вектор, состоящий из #N/A! если решения нет и вектор, состоящий из #ЧИСЛО! если существует бесконечное число решений.

По умолчанию каждая из этих функций предполагает, что запись с абсолютным значением меньше 0,0001 эквивалентна нулю. Это необходимо, поскольку малые значения не обрабатываются как нуль в алгоритме исключения Гаусса, описанном выше. Вы можете изменить это значение по умолчанию на другое, вставив второй параметр в любую из этих функций: например, ELIM(R1, prec ) или LINEQU(R1, prec ). Таким образом, ELIM(R1) = ELIM(R1, 0,0001).

Инструмент анализа данных реальной статистики : инструмент анализа данных «Решение набора линейных уравнений», содержащийся в пакете ресурсов «Реальная статистика», обеспечивает эквивалентную функциональность для LINEQU и ELIM. Чтобы использовать этот инструмент, введите Ctrl-m и выберите в меню «Решить набор линейных уравнений». Когда появится диалоговое окно, заполните Входной диапазон (тем же диапазоном, что и R1 выше). Выбор «Показать только решение»

---