Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: очно-заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Эконометрика



Группа М21Э371в
Студент
П.А. Чуглина


МОСКВА 2023

1.Укажите основные этапы эконометрического исследования.

Ответ: Основные этапы эконометрического исследования:

- постановка проблемы (используется экономическая теория);

- подготовка информации (используется статистика);

- формулировка вида моделей количественных показателей экономики и их взаимосвязей (используются экономическая теория и математика);

- оценка параметров и анализ качества моделей (используются математика, и, в частности, математическая статистика);

-анализ и прогнозы количественных показателей экономики с помощью «удачных», с точки зрения статистических критериев, моделей, экономическое толкование результатов (используются экономическая теория и математика).


2.Назовите виды аналитических зависимостей, наиболее часто используются при построении моделей.


Ответ: Наиболее часто используются линейная и степенная функции.

В линейной модели параметры bi при факторах хi характеризуют величину среднего изменения зависимой переменной y с изменением соответствующего фактора хi на единицу, в то время как значения остальных факторов остаются неизмененными.

В степенной модели параметры bj при факторах хi являются коэффициентами эластичности. Они показывают, на сколько процентов в среднем изменяется зависимая переменная y при изменении соответствующего фактора хi на 1 % в условиях неизменности действия других факторов. Этот вид уравнения регрессии получил наибольшее 

---

распространение в производственных функциях, в исследованиях спроса и потребления.


3.Охарактеризуйте функции, которые чаще всего используются для построения уравнения парной регрессии.


Ответ: В парной регрессии выбор вида математической функции ŷх = f(x) может быть осуществлен тремя методами:

1. графическим;

2. аналитическим, т.е. исходя из теории изучаемой взаимосвязи;

3. экспериментальным.

Класс математических функций для описания связи двух переменных достаточно широк. Основными являются следующие:

1. ŷх = a + b*x;

2. ŷх = a + b/x;

3. ŷх = a*xb;

4. ŷх = a + b*x + c*x2;

5. ŷх = a + b*x + c*x2 + d*x3;

6. ŷх = a*bx.


4.Укажите, по какой формуле вычисляется выборочный коэффициент парной корреляции r_xy .


Ответ: Выборочный коэффициент корреляции является одним из основных показателей тесноты связи между двумя переменными. При изучении зависимости переменной Y от переменной Х выборочный коэффициент корреляции обозначается как rxy. При изучении зависимости переменной Х от переменной Y выборочный коэффициент корреляции обозначается как ryx.

Выборочный коэффициент корреляции является оценкой коэффициента корреляции Pxy генеральной совокупности.

Выборочный парный коэффициент корреляции ryx:



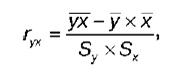
где ух – среднее арифметическое произведения факторной и результативной переменных:



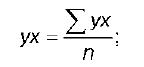
S y – выборочное среднеквадратическое отклонение результативной переменной у , показывающее, на сколько единиц в среднем отклоняются значения результативной переменной уот ее среднего значения y–:



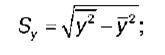
у 2 – среднее значение из квадратов значений результативной переменной у :

---

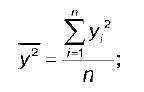
Выборочный коэффициент корреляции обладает следующими свойствами:

1) по абсолютной величине выборочный коэффициент корреляции не превосходит единицы: | r yx | ≤ 1, или –1 ≤ ryx ≤ 1;

2) если ryx = 0, т. е. выборочный коэффициент корреляции равен нулю, то переменные Y и Х не связаны статистической зависимостью. В этом случае проведение регрессионного анализа между исследуемыми переменными считается нецелесообразным;

3) если |ryx| = 1, т. е. выборочный коэффициент корреляции по абсолютной величине равен единице, то наблюдаемые значения исследуемых переменных связаны линейной функциональной зависимостью;

4) если выборочный коэффициент корреляции принадлежит интервалу от нуля до единицы, то связь между исследуемыми переменными прямая; если же выборочный коэффициент корреляции принадлежит интервалу от нуля до минус единицы, то связь между исследуемыми переменными обратная.
5.Объясните сущность метода анализа динамического ряда.


Ответ: Комплексный анализ динамических рядов, как правило, включает не только расчет характеристик интенсивности изменения уровней ряда при переходе от одного момента или промежутка времени к другому (абсолютных приростов, коэффициентов и темпов роста и прироста), а также нахождение обобщенных средних характеристик (среднего уровня ряда, средних темпов роста и прироста), но и выявление основных закономерностей в развитии динамического ряда. Определение тенденции развития, построение модели, описывающей изменение явления во времени, прогнозирование явления - все это важнейшие задачи при изучении динамических рядов экономических и социальных показателей.

На формирование уровней динамического ряда влияет множество различных факторов, которые по характеру воздействия можно объединить в три группы:

1. 
   действующие долговременно и определяющие основную тенденцию развития явления;
   
2. 
   действующие периодически - сезонные и циклические колебания;
   
3. 
   вызывающие случайные колебания уровней динамического ряда.
   

---

Соответственно, для анализа закономерности изменения уровней ряда динамики во времени применяют следующую модель:



где Тt - основная тенденция ряда (тренд);

St - циклические (в частности, сезонные) колебания;

еt - случайные колебания.

В аддитивной модели ряд динамики представлен как сумма перечисленных компонент [yt = Tt + St + et], в мультипликативной модели - как их произведение [   ]. В дальнейшем будем исходить из предположения мультипликативной формы связи между компонентами ряда динамики.

Тенденцией развития, или трендом, называется сформировавшееся направление развития явления во времени под воздействием постоянно действующих факторов. Судить о наличии тенденции в динамическом ряду на основе его визуального анализа можно лишь тогда, когда четко видно, что при переходе от одного момента времени к другому уровни ряда возрастают или убывают. Однако, как правило, нельзя сразу сказать, есть или нет тенденция в изменении уровней динамического ряда. Для этого применяются специальные методы.

К методам выявления основной тенденции развития динамического ряда (Тt) относятся:

• 
  метод укрупнения интервалов;
  
• 
  метод скользящей средней;
  
• 
  аналитическое выравнивание динамических рядов.
  

Задачи:

1. 
   Рассчитать коэффициенты для различных видов зависимостей. Исходные данные в табл.3
   

Таблица 3. Регрессионный анализ.

Значения вел X № варианта	10	20	30	40	50
1	7,38	18,15	44,64	109,79	270,06
2	30	50	70	90	110
3	23,94	58,95	99,87	145,16	194,01
4	126,19	54,92	33,77	23,91	18,29
5	166,44	55,41	18,44	6,14	2,04

---

Решение:

Система нормальных уравнений.


 Линейная зависимость

Для расчёта параметров регрессии построим расчётную таблицу

х	у	x2	y2	x*y
10	7,38	100	54,4644	73,8
20	18,15	400	329,4225	363
30	44,64	900	1992,7296	1339,2
40	109,79	1600	12053,8441	4391,6
50	270,06	2500	72932,4036	13503
150	450,02	5500	87362,8642	19670,6

Для наших данных система уравнений имеет вид
   Домножим 1-е уравнение системы на (-30), получим систему, которую решим методом алгебраического сложения.
   Откуда   Найдём   :
       Уравнение линейной регрессии:

---

Смотрите также файлы

• Народничество.docx

• Диплом о присвоении дополнительной квалификации Мастер делового администрирования Master of Business Administration (mba).docx

• Система социального обеспечения всегда занимала важное место в жизни государства и общества.docx

• 1 Ханьчжоу Бей 4 1 Проектирование моста 4.doc

• Что такое глобальные проблемы Глава Демографическая проблема Глава Экологические проблемы.docx