Практическое задание 6

Тема 2.5. Сложное движение точки и твердого тела

Задание

Круглая пластина (рис. 6.1) радиусом 0,1(С + 1) (м) вращается вокруг неподвижной оси, проходящей перпендикулярно рисунку через нижнюю точку О по закону Пt² – Гt (рад). По окружности пластины движется точка М из точки А. Закон ее относительного движения – длина дуги между точками А и М равна 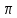(П + 1)t² (м). Определите абсолютную скорость и ускорение точки М в момент времени 1 с.



Рис. 6.1

Рекомендации по выполнению задания 6

1. 
   Выделите точку, совершающую сложное движение.
   
2. 
   Проведите анализ движения точки – выделите относительное, переносное, абсолютное движения.
   
3. 
   Изобразите точку на рисунке в заданный момент времени.
   
4. 
   Определите относительную скорость точки:
   
   1. 
      Постройте траекторию точки в относительном движении.
      
   2. 
      Постройте вектор относительной скорости точки, определите его модуль.
      
5. 
   Определите переносную скорость точки:
   
   1. 
      Постройте траекторию точки тела, совпадающей с исследуемой точкой в заданный момент времени в переносном движении точки.
      
   2. 
      Постройте вектор переносной скорости точки, определите его модуль.
      
6. 
   Определите абсолютную скорость точки:
   
   1. 
      Постройте вектор абсолютной скорости точки либо по касательной к траектории в абсолютном движении, либо как диагональ параллелограмма, построенного на векторах относительной скорости точки и переносной скорости точки.
      
   2. 
      Определите модуль либо по теореме Пифагора, либо по теореме косинусов.
      
7. 
   Определите относительное ускорение точки:
   
   1. 
      Постройте траекторию точки в относительном движении.
      
   2. 
      Постройте вектор относительного ускорения точки, определите его модуль.
      
8. 
   Определите переносное ускорение точки:
   
   1. 
      Постройте траекторию точки тела, совпадающей с исследуемой точкой в заданный момент времени в переносном движении.
      
   2. 
      Постройте вектор переносного ускорения точки, определите его модуль.
      
9. 
   Определите абсолютное ускорение точки:
   
   1. 
      Постройте вектор абсолютного ускорения точки как геометрической суммы трех ускорений – относительного, переносного и поворотного.
      
   2. 
      Определите модуль абсолютного ускорения точки.
      

---

Бланк выполнения задания 6

1. Записываются данные задания.

2. Представляется рисунок, на котором показана точка, совершающая сложное движение на теле, в заданный момент времени.

3. Находятся все скорости точки.

4. Находятся все ускорения точки.

5. На рисунке показываются все векторы скоростей и ускорений точки.

6. Записывается ответ.

---

Смотрите также файлы

• Уголовноисполнительная политика это часть государственной политики в сфере борьбы с преступностью.docx

• Методические указания Профиль Безопасность технологических процессов и производств.docx

• Вид работы Курсовая работа Название дисциплины Гражданское право Тема Доверенность правовая характеристика Фамилия студента Попова Имя студента.doc

• Вы зашли под именем Белозерцева Наталья Михайловна (Выход) анпоо "нспк".pdf

• Кейс 3 Задание Постройте дерево целей организации на предстоящую перспективу и определите тип инновационной стратегии организации с описанием факторов, влияющих на ее выбор. Решение.docx