Файл: Лабораторная работа 2 По дисциплине Теория языков программирования и методы трансляции Выполнил Группа.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 11
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство связи
Сибирский Государственный Университет Телекоммуникаций и Информатики
Межрегиональный центр переподготовки специалистов
Лабораторная работа №2
По дисциплине:
«Теория языков программирования и методы трансляции»
Выполнил:
Группа:
Вариант: № 5
Проверил: Бах Ольга Анатольевна
Новосибирск, 2018 г
Постановка задачи
Моделирование работы ДКА
Пусть регулярный язык задаётся конечным автоматом – ДКА (теоретический материал разделов 1.5, 2.2). Написать программу, которая будет проверять по заданному автомату вводимую цепочку и делать вывод о том, принадлежит ли она рассматриваемому регулярному языку. В случае отрицательного ответа необходимо давать пояснение, по какой причине цепочка не принадлежит языку – например, “в цепочке присутствуют посторонние символы”, “после прочтения цепочки автомат не пришёл в конечное состояние” и т.п. Исходный автомат вводить с клавиатуры в соответствии с определённым форматом. Ввод цепочек также производить с клавиатуры.
Дополнительно:
Предоставить пользователю возможность не только вводить данные с клавиатуры, но и загружать автомат из файла (выбор – в соответствующем пункте меню или нажатием кнопки в исходном окне программы). При этом следует накладывать определённые ограничения на формат файла и производить соответствующие проверки во избежание загрузки некорректных данных.
Также по желанию пользователя результаты помимо вывода на экран сохранять в файле. Выбор – аналогично загрузке данных.
Описание входных данных программы и её результатов
На вход программы подаётся ДКА (множество состояний, алфавит языка, начальное состояние, множество заключительных состояний, функция переходов в виде таблицы) и проверяемая цепочка символов (может вводиться многократно, т.е. возможно проверить любое количество цепочек). При этом в проверяемую цепочку могут входить и символы, не принадлежащие алфавиту языка; цепочка может быть и пустой.
Программа предоставляет пользователю возможность изменять начальное и конечные состояния с сохранением введённой функции переходов для заданного автомата.
Описание основных переменных, а также основных блоков и подпрограмм
Q - множество состояний.
V - множество символов алфавита.
F - множество конечных состояний.
T - таблица переходов задается двухмерным индексным массивом.
int F - множество конечных состояний.
T[MAX_SYMB_COUNT][MAX_SYMB_COUNT] - таблица пере-ходов.
q0 - начальное состояние.
nQ - число состояний.
nV - число символов в алфавите.
nF - число заключительных состояний.
function SymbolSearch ищет символ, указатель которого ей передается в качестве параметра Symb.
function SymbolIdentify читает строку по указателю Str и ищет сов-падения с символами, находящимися в массиве M[][MAX_SYMB_LENGHT].
function VerifyString без параметров. Запрашивает ввод цепочки и осуществляет проверку введенной цепочки по алгоритму решения задачи.
Алгоритм решения задачи
На первом этапе устанавливается начальное состояние автомата и указатель (головка) на первый символ цепочки. Алгоритм проверки цепочки заключается в чтении символа из входной цепочки и, в зависимости от полученной пары состояние/символ, по таблице перехода определяется новое состояние автомата. Этот процесс осуществляется в цикле до тех пор, пока не закончатся символы в цепочке, или будет прочитан неизвестный символ, или для полученной комбинации состояние/символ значение функции не определено. После прочтения всей цепочки проверяется состояние, в которое пришел автомат, если оно принадлежит множеству заключительных, то цепочка считается допущенной.
Текст программы:
(main.cpp)
#include
#include
#include
#include
#include "main.h"
char Q[MAX_SYMB_COUNT][MAX_SYMB_LENGHT], // множество состояний
V[MAX_SYMB_COUNT][MAX_SYMB_LENGHT]; // множество символов алфавита
int F[MAX_SYMB_COUNT], // множество конечных состояний
T[MAX_SYMB_COUNT][MAX_SYMB_COUNT], // таблица переходов
q0, // начальное состояние
nQ, // число состояний
nV, // число символов в алфавите
nF; // число заключительных состояний
int main()
{
while(true)
{
system("cls");
puts("1 - Ввод ДКА");
puts("2 - Выход");
switch(_getch())
{
case '1':
{
EnterAutomate();
bool end = false;
while(!end)
{
system("cls");
puts("1 - Проверить цепочку");
puts("2 - Изменить начальное состояние");
puts("3 - Изменить множество конечных состояний");
puts("4 - Назад");
switch(_getch())
{
case '1':
{
int Result = VerifyString();
ResultMessage(Result);
}
break;
case '2':
{
system("cls");
puts("Начальное состояние");
q0 = ControlEnterSymbol(Q, nQ);
}
break;
case '3':
{
system("cls");
puts("Ввод конечных состояний");
EnterFinalStates();
}
break;
case '4':
end = true;
}
}
}
break;
case '2':return 1;
}
}
}
// Функция ищет символ Symb в массиве M и возвращает его индекс, если символ не найден, функция вернет размер массива
int SymbolSearch(char M[][MAX_SYMB_LENGHT], int Size, char *Symb)
{
int i = 0;
while (i< Size)
{
if (strcmp(M[i], Symb) == 0) break;
i++;
}
return i;
}
// Функция вводит символы разделенные запятыми из строки Str в массив M, возвращает количество веденных символов
int EnterScores(char M[][MAX_SYMB_LENGHT], int max)
{
char Str[MAX_STR_LENGHT];
char *pNextToken = NULL;
int i = 0;
printf("Введите через запятую множество:\n>> ");
gets_s(Str, MAX_STR_LENGHT-1);
char * pToken = strtok_s(Str, ", ", &pNextToken);
while (pToken)
{
strcpy_s(M[i], pToken);
i++;
if(i == max) break;
pToken = strtok_s('\0', ", ", &pNextToken);
}
return i;
}
// Ввод символа
// Ввод будет запрашиваться пока не будет введен символ принадлежащий множеству М
// Функция возвращает индекс введенного символа
int ControlEnterSymbol(char M[][MAX_SYMB_LENGHT], int Size)
{
char Str[MAX_SYMB_LENGHT];
int index;
while (true)
{
printf(">> ");
gets_s(Str, MAX_SYMB_LENGHT-1);
if ((index = SymbolSearch(M, Size, Str)) == Size)
printf("%s - недопустимый символ!\n", Str);
else break;
}
return index;
}
// Ввод множества конечных состояний
void EnterFinalStates()
{
bool end = false;
char Symb[MAX_SYMB_COUNT][MAX_SYMB_LENGHT];
while (!end)
{
end = true;
int i = 0;
nF = EnterScores(Symb, MAX_SYMB_LENGHT);
while(i < nF)
{
if ((F[i] = SymbolSearch(Q, nQ, Symb[i])) == nQ)
{
printf("Символ %s не принадлежит множеству состояний!\n", Symb[i]);
end = false;
}
i++;
}
}
}
//Функция вывода таблицы переходов
void TableView()
{
for ( int i=0; i
printf("\t%s", V[i]);
printf( "\n");
for (int i=0; i
{
printf("%s", Q[i]);
for (int j=0; j
{
printf("\t");
if (T[i][j] != -1) printf("%s", Q[T[i][j]]);
else printf("-");
}
printf ( "\n" );
}
}
// Ввод таблицы переходов
void EnterTable ()
{
char Str[MAX_SYMB_LENGHT];
memset(T, -1, sizeof(int)*MAX_SYMB_COUNT*MAX_SYMB_COUNT);
for (int i=0; i
for (int j=0; j
{
system("cls");
puts("Ввод таблицы переходов");
TableView();
while (true)
{
printf("f(%s, %s) = ", Q[i], V[j]);
gets_s(Str, MAX_SYMB_LENGHT-1);
if(Str[0] == '\0') break;
if((T[i][j] = SymbolSearch(Q, nQ, Str)) == nQ)
printf("Символ %s не принадлежит множеству состояний!\n", Str);
else break;
}
}
system("cls");
puts("Ввод таблицы переходов");
TableView();
puts("Ввод таблицы переходов завершен!");
system("pause");
}
// Функция ввода ДКА
int EnterAutomate()
{
system("cls");
puts("Ввод состояний");
nQ = EnterScores(Q, MAX_SYMB_COUNT);
puts("Ввод алфавита языка");
nV = EnterScores(V, MAX_SYMB_COUNT);
puts("Начальное состояние");
q0 = ControlEnterSymbol(Q, nQ);
puts("Ввод конечных состояний");
EnterFinalStates();
EnterTable ();
return 1;
}
// Идентификация первого символа в строке
int SymbolIdentify(char M[][MAX_SYMB_LENGHT], int Size, char **Str)
{
char Symb[MAX_SYMB_LENGHT];
int ind = Size;
char *pNextSymb = *Str;
for(unsigned char i=1; (i<=strlen(*Str))&&(i < MAX_SYMB_LENGHT); i++)
{
strncpy_s(Symb, MAX_SYMB_LENGHT, *Str, i);
if(SymbolSearch(M, Size, Symb) < Size)
{
ind = SymbolSearch(M, Size, Symb);
pNextSymb = *Str + i;
}
}
*Str = pNextSymb;
return ind;
}
// Функция проверки цепочки
int VerifyString()
{
char Str[MAX_STR_LENGHT];
system("cls");
TableView();
puts("Введите цепочку символов для проверки:");
gets_s(Str, MAX_STR_LENGHT-1);
int q = q0; // устанавливаем начальное состояние
int a;
char *w = Str; // устанавливаем указатель на начало строки
while(*w) // пока не дойдем до конца строки
{
printf("(%s, %s)\n", Q[q], w); // выводим МО автомата
if((a = SymbolIdentify(V, nV, &w)) == nV) return UNDEFINED_SYMBOL; // если символ не распознан возвращаем ошибку
q = T[q][a]; // переходим в новое состояние
if(q == -1) return UNDEFINED_STATE; // проверяем состояние, если оно не определено, возвращаем ошибку
}
printf("(%s, lam)\n", Q[q], w);
for(int i=0; i
if(q == F[i]) return SUCCESS; // если оно заключительное, то цепочка прошла проверку
return NO_FINAL_STATE; // если состояние не заключительное, возвращаем ошибку
}
void ResultMessage(int Result)
{
if(Result != SUCCESS)
{
puts("Цепочка не принадлежит языку, определяемому данным автоматом! Причина");
switch(Result)
{
case UNDEFINED_SYMBOL:
puts("Недопустимый символ");
break;
case UNDEFINED_STATE:
puts("Неопределенное значение для функции перехода");
break;
case NO_FINAL_STATE:
puts("Автомат не пришел в конечное состояние");
}
}
else puts("Цепочка принадлежит языку, определяемому данным автоматом");
system("pause");
}
Результаты работы программы
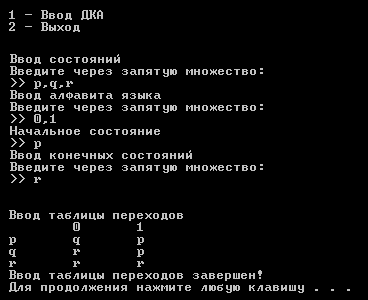
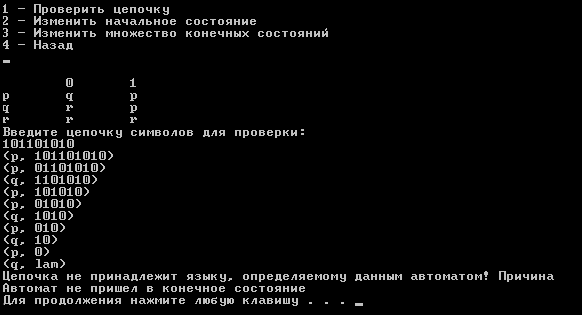
Контрольные вопросы
-
Как поведёт себя программа, если при вводе таблицы переходов ДКА сделать (случайно или преднамеренно) ошибку – например, ввести несуществующее состояние?
Ответ: Если при вводе таблицы переходов ДКА сделать ошибку, то программа предложит повторный ввод.
-
Все ли ячейки таблицы переходов исходного ДКА обязательно должны быть заполнены или можно использовать не полностью определённый ДКА?
Ответ: При вводе пустой строки, ячейка таблицы переходов останется неопределённой и ДКА получится не полностью определённый.
-
В каком случае ДКА распознаёт пустую цепочку как цепочку языка?
Ответ: в случае, если начальное состояние принадлежит множеству конечных состояний.