ЛАБОРАТОРНАЯ РАБОТА № 5.03
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА И СИЛЫ ТРЕНИЯ В ОПОРЕ
Приборы и принадлежности: 1. маховик со шкивом,

2. масштабная линейка,

3. штангенциркуль,

4. секундомер,

5. груз с нитью.
1. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
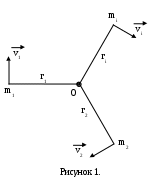
При вращении твердого тела под действием вращающего момента изменяется лишь кинетическая энергия вращения. Вычислим ее как сумму кинетических энергий отдельных элементов абсолютно твердого тела. Разобьем твердое тело на элементы столь малые, что их размерами можно пренебречь, и будем каждый такой элемент принимать за материальную точку с массой равной массе элемента (на рис. 1 показаны только три такие точки). Точки m₁, m₂, m₃,…, m_i, находящиеся на расстояниях r₁, r₂, r₃,…, r_i от оси О, движутся с различными линейными скоростями v₁, v₂, v₃,…, v_i. Обозначая кинетическую энергию всего тела через Т, будем иметь:

(1)

Равномерное вращение твердого тела характеризуется его постоянной угловой скоростью , которая равна отношению угла поворота к соответствующему времени:

, (2)

где  – угол, на который повернулось тело за t секунд.

Линейная скорость точки v связана с угловой скоростью:

v =   r, (3)

где r – расстояние точки от оси вращения.

Примем эту связь к рассмотренным нами точкам:

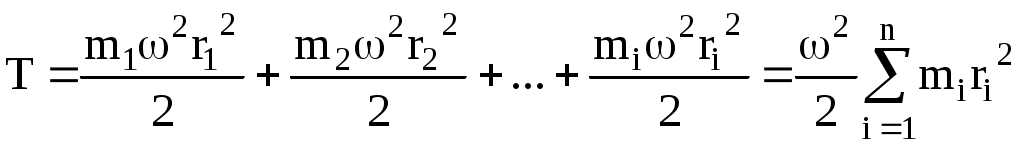. (4)

Величину = J (5)

называют моментом инерции тела относительно оси вращения тела О (рис. 1). С учетом (5) кинетическая энергия вращающегося тела выразится:

(6)

Сопоставим полученное нами выражение (6) для кинетической энергии вращающегося тела с выражением для кинетической энергии тела, движущегося поступательно:



Очевидно, что момент инерции вращающегося тела имеет такое же физическое значение при вращательном движении, как масса тела при его поступательном движении, являющаяся мерой инертности тела. Анализ выражений (5) показывает, что если мы будем иметь только одну вращающуюся точку с массой m, находящуюся на расстоянии r от оси вращения, то ее момент инерции будет равен:

---

J₁ = mr₁². (7)

Все слагаемые в формуле (5) суть моменты инерции отдельных материальных точек. Следовательно, момент инерции тела равен сумме моментов инерции его материальных точек.

Вычисление момента инерции тела – задача очень сложная, так как приходится находить сумму бесконечно большого числа малых слагаемых. Для тел правильной формы эта задача решается методом интегрального исчисления. Существует ряд методов, позволяющих определить момент инерции тела экспериментально. Один из них будет использован в настоящей работе.

Момент инерции твердого тела связан с вращающим моментом, действующим на тело, основным законом динамики:

M = J  , (7)

где  – угловое ускорение, или



где М – сумма моментов сил, действующих на тело;

 – угловая скорость вращения.

Если М = 0, то

или J = const. (9)

Величина J называется моментом количества движения. Таким образом, если на вращающееся тело не действует вращающий момент, то оно будет вращаться неопределенно долго, сохраняя постоянный имеющийся у него момент количества движения.

Можно доказать, что этот закон справедлив и для системы тел. На замкнутую систему тел внешние силы вообще не действуют. Поэтому результирующий (главный) момент сил относительно любой оси тождественно равен нулю. Итак, закон сохранения момента количества движения гласит:

В замкнутой системе тел момент количества движения всей системы относительно любой неподвижной оси не изменяется в процессе движения.

Этот закон может быть обобщен на любую не замкнутую систему тел. Если результирующий момент всех сил, приложенных к системе, относительно какой-либо неподвижной оси тождественно равен нулю, то момент импульса системы относительно той же оси изменяется со временем.

Можно показать, что в замкнутой системе тел, силы взаимодействия между которыми консервативны, отсутствуют взаимные превращения механической энергии в другие виды энергии (не механические). Такие системы называются замкнутыми консервативными, причем для них справедлив закон сохранения энергии в механике:

---

Механическая энергия замкнутой консервативной системы не изменяется в процессе движения, т. е.

T + W_n = const. (10)

В замкнутой системе справедлив принцип сохранения энергии: запас энергии в замкнутой системе остается неизменным при всех происходящих в ней процессах.

Вследствие того, что взаимодействие между телами и частицами является всеобщим (универсальным) свойством материала, понятие замкнутой системы является лишь идеализацией реальной действительности, так как окружающие нас тела всегда взаимодействуют между собой и при этом отдают или получают энергию в тех или иных формах. Однако все бесчисленные эксперименты показывают, что энергия не возникает и не исчезает при всех процессах происходящих в природе, она лишь превращается из одной формы в другую. Поэтому правильнее называть этот всеобщий (универсальный) закон природы законом сохранения и превращения энергии.
2. ТЕОРИЯ МЕТОДА И УСТАНОВКИ
М 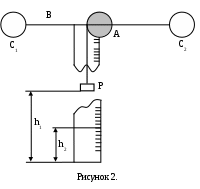омент инерции махового колеса и силу трения в опоре можно определить при помощи прибора, изображенного на рисунке 2. Прибор состоит из махового колеса А, насаженного на вал В. Вал установлен на шарикоподшипниках С₁ и С₂. Маховое колесо приводится во вращательное движение грузом Р. Груз Р на какой-то высоте обладает потенциальной энергией mgh₁, где m – масса груза. Если предоставить грузу Р возможность падать, то потенциальная энергия mgh₁ перейдет в кинетическую энергию поступательного движения , кинетическую энергию вращательного движения и на работу A = fh по преодолению силы трения в опоре. По закону сохранения и превращения энергии:

(11)

где f – сила трения в опоре.

Движения груза равноускоренное без начальной скорости, поэтому ускорение а и скорость v соответственно равны:

---

(12)

где t – время опускания груза с высоты h₁.

Найдем скорость (угловую) махового колеса по формуле:

(13)

где r – радиус вала.

Сила трения вычисляется следующим образом: колесо, вращаясь по инерции, поднимает груз на высоту h₂ > h₁, и потенциальная энергия его на высоте h₂ будет mgh₂. Уменьшение потенциальной энергии при подъеме груза равно работе по преодолению силы трения в опорах С₁ и С₂, т. е.

mgh₁ - mgh₂ = f (h₁ + h₂), откуда

. (14)

Подставляя в формулу (14) значения v, , f, получим окончательное выражение для вычисления момента инерции махового колеса:

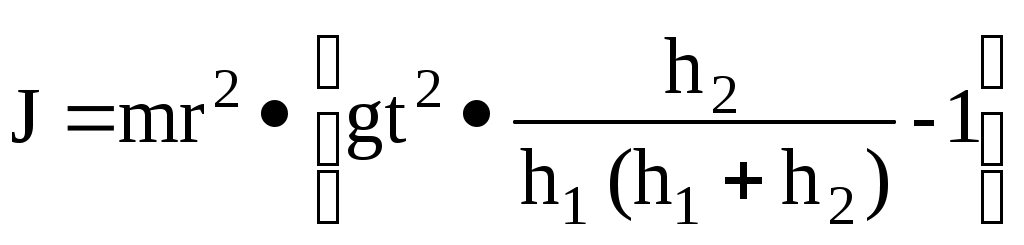. (15)
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Наматываем на вал В нить и поднимаем груз до высоты h₁ (до максимальной).

2. Опускают груз Р и измеряют время падения груза с высоты h₁, включая секундомер.

3. Спустившись, груз по инерции поднимается от пола на определенную высоту h₂, которую и замеряют масштабной линейкой.

4. Не менее трех раз измеряют радиус вала r штангенциркулем.

5. Опыты, описанные в пункте 2, проделывают десять раз, опуская груз Р все десять раз с одной и той же высоты h₁.

6. Опытные данные заносят в таблицу.

7. Взяв груз Р другой массы, повторяют все опыты заново.
4. ОБРАБОТКА РЕЗУЛЬТАТОВ
Сначала находят средние значения времени падения t_ср и средние значения высоты поднятия груза h_ср. Вычисляют среднее значение момента инерции J по формуле (15); величина массы грузов задана.

Затем находят абсолютную погрешность измерения момента инерции J. Для этой цели вычисляют сначала относительную погрешность:

Из формулы (15) получаем:

(16)

Погрешностью можно пренебречь, т. к. она по сравнению с остальными мала. Погрешность h₁ очень мала, ею можно также пренебречь, т. е. h₁ = 0, тогда и

---

. Учитывая все эти замечания, будем иметь:

.

Погрешности m, r, t определяют, исходя из точности приборов, h₂ – как при прямых измерениях. Вычислив относительную погрешность Е, находят

J = E  J.

Записывают окончательный результат:

J_ист = (J_ср  J_ср) кг  м².
ТАБЛИЦА ЗАПИСЕЙ НАБЛЮДЕНИЙ

m = … (кг) r = … (м)

m = … (кг) r = … (м)
Для груза m₁

№ п. п.	h1, м	h2, м	t, c	f, H	J1, кг  м2	J1, кг  м2		J1ист, кг  м2
1
2
…
10
		h1ср	t1ср		J1ср	J1ср

Для груза m₂

№ п. п.	h1, м	h2, м	t, c	f, H	J1, кг  м2	J1, кг  м2		J1ист, кг  м2
1
2
…
10
		h2ср	t2ср		J2ср	J2ср

---

Смотрите также файлы

• 2. Есть ли у вас привычка договаривать фразы, начатые вашим собеседником, поскольку вам кажется, что вы угадали его мысль, а говорит он слишком медленно.docx

• Прохождение программы по итогам 2 триместра 20212022.docx

• 4 3 Разработка модели угроз безопасности информации.docx

• Государственные органы Еврейской автономной области регулирующие сферу туризма и гостеприимства.pptx

• Тема Современные методы лечения поверхностного и среднего кариеса. Задания для проверки исходного уровня 1.docx