ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Что такое ОДУ?
Обыкновенное дифференциальное уравнение (ОДУ) - это уравнение, содержащее неизвестную функцию одного вещественного или комплексного переменного x, его производные и некоторые заданные функции x. Неизвестная функция обычно представлена переменной (часто обозначаемой y), которая, следовательно, зависит от x. Таким образом, x часто называют независимой переменной уравнения.
-
ОДУ каких типов решает MathCAD?
С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, причем как функции, так и аргументы могут быть и действительными, и комплексными.
-
Из каких частей состоит вычислительный блок given-Odesolve?
Применение функции Odesolve требует записи вычислительного блока, состоящего из трех частей:
1) ключевого слова Given (Дано);
2) дифференциального уравнения и начальных или граничных условий к нему;
3) функции оdesolve (x, xk, n) (решение ОДУ), где x – имя переменной, относительно которой решается уравнение; xk – конец интервала интегрирования (начало интервала интегрирования указано ранее, в начальных условиях); n – необязательный внутренний параметр, определяющий число шагов интегрирования, на которых решается дифференциальное уравнение.
-
Каким образом при решении системы ОДУ можно выбрать метод решения?
Одно обыкновенное дифференциальное уравнение или система ОДУ имеет единственное решение, если помимо уравнения определенным образом заданы начальные или граничные условия. Имеется два типа задач, для которых возможно численное решение ОДУ с помощью MathCAD:
- задачи Коши, для которых определены начальные условия на искомые функции, т.е. заданы значения этих функций в начальной точке интервала интегрирования уравнения;
- краевые задачи, для которых заданы определенные соотношения сразу на обеих границах интервала.
Из дифференциальных уравнений в частных производных есть возможность решать только уравнения с двумя независимыми переменными: одномерные параболические и гиперболические уравнения, такие как уравнения теплопроводности
, диффузии, волновые уравнения, а также двухмерные эллиптические уравнения (уравнения Пуассона и Лапласа).
В MathCAD нет универсальной функции для решения дифференциальных уравнений, а есть около двадцати функций для различных видов уравнений, дополнительных условий и методов решения. Эти функции можно найти в библиотеке Insert/Function, категория “Differential Equation Solving (решение дифференциальных уравнений).
-
Какие функции предназначены для решения дифференциальных уравнений и их систем?
Чтобы аналитически продифференцировать выражение по некоторой переменной, выделите в нем эту переменную и выберите команду Symbolics / Variable /Differentiate (Символика / Переменная / Дифференцировать).
-
Какие параметры необходимо задать для решения дифференциальных уравнений и их систем?
Для того чтобы аналитически найти производную функции f (х) в Mathcad:
1. Задайте функцию f (х).
2. Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак >.
3. В появившихся местозаполнителях оператора дифференцирования введите функцию, зависящую от аргумента х, т. е. f(х), и имя самого аргумента х.
4. Введите оператор <->> символьного вычисления для получения ответа
-
Как проинтегрировать дифференциальное уравнение первого порядка?
Дифференциальное уравнение первого порядка в общем случае содержит:
1) независимую переменную;
2) зависимую переменную (функцию);
3) первую производную функции:
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или (и) «игрек», но это не существенно – важно чтобы в ДУ была первая производная, и не было производных высших порядков – y’, y”’ и т.д.
Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество всех функций, которые удовлетворяют данному уравнению. Такое множество функций часто имеет вид
– произвольная постоянная), который называется общим решением дифференциального уравнения.
-
Какие параметры необходимо задать для решения дифференциальных уравнений n порядка?
Mathcad позволяет численно определять производные высших порядков, от 3-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка в точке х, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора производной необходимо применить оператор м-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры нажатием клавиш
-
Какая система называется жесткой?
Жёсткой системой обыкновенных дифференциальных уравнений (ОДУ) называется (нестрого говоря) такая система ОДУ, численное решение которой явными методами (например, методами Рунге — Кутты или Адамса) является неудовлетворительным из-за резкого увеличения числа вычислений (при малом шаге интегрирования) или из-за резкого возрастания погрешности (так называемого, взрыва погрешности) при недостаточно малом шаге. Для жёстких систем характерно то, что для них неявные методы дают лучший результат, обычно несравненно более хороший, чем явные методы.
-
Какие функции используют для решения жесткой системы дифференциальных уравнений?
Еще одна задача, связанная с нахождением частных производных векторной функции, заключается в вычислении якобиана (или определителя матрицы Якоби) — матрицы, составленной из частных производных векторной функции по всем ее аргументам. Эта задача встречается в различных областях математики, например, применительно к жестким дифференциальным уравнениям. Приемы вычисления якобиана векторной функции f (х) векторного аргумента х. В нем для определения частных производных якобиана каждый i-й скалярный компонент f (x)i дифференцируется символьным процессором Mathcad.
-
Какое отличие в написании функций для решения только в конечной точке?
Для того чтобы численно продифференцировать функцию f (х) в некоторой точке, следует использовать оператор численного вывода (вместо символьного):
1. Определите точку х, в которой будет вычислена производная, например, х:=1.
2. Введите оператор дифференцирования и обычным образом введите имена функции и аргумента в место заполнители.
3. Введите оператор = численного вывода результата.
-
Какие выделяют типы уравнений в частных производных?
Уравнения первого порядка. Уравнения первого порядка называются также уравнениями переноса. Это объясняется тем, что такие уравнения описывают процессы переноса частиц в средах, распространения возмущений и т. п.
Его решение представляет интерес не только с практической точки зрения; в еще большей степени это уравнение полезно при разработке и исследовании разностных схем.
Будем считать, что искомая функция
зависит от времени
и одной пространственной переменной х. Тогда линейное уравнение переноса может быть записано в виде
.Здесь
‑ скорость переноса.Уравнения второго порядка. Линейным уравнением в частных производных второго порядка называется соотношение между функцией
или
и ее частными производными вида.
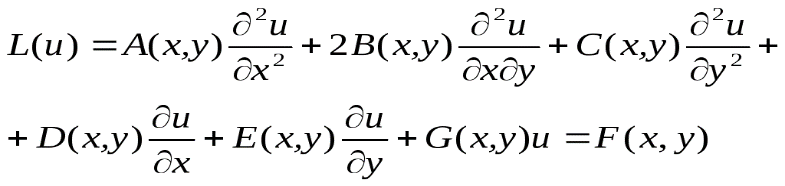(1)Если переменная функция
зависит от
и
, то уравнение может быть записано следующим образом:
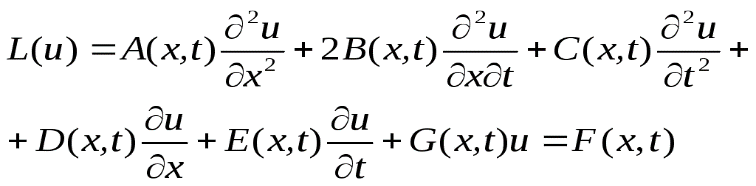(2)-
С помощью каких функций решаются уравнения в частных производных?
Чтобы вычислить производную порядка выше 5-го численно, можно последовательно применить несколько раз оператор м-й производной, подобно тому, как производится отыскание кратных интегралов. Однако следует помнить о том, что численное определение производных высших порядков производится тем же вычислительным методом Риддера, что и для первых производных. Поскольку, как уже было сказано, для первой производной этот метод обеспечивает точность до 7—8 значащих разрядов числа, при повышении порядка производной на каждую единицу точность падает примерно на один разряд.