Добавлен: 26.10.2023
Просмотров: 86
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное автономное профессиональное образовательное учреждение
Челябинской области “Политехнический колледж”
Специальность: Машинист локомотива
Курс: 2
Студент: Черноморец А.Н.
Дисциплина: ОУД.04 Математика
Фракталы: Геометрия красоты
Индивидуальный проект
Руководитель: преподаватель высшей категории Ларкина Е.В.
Оценка:____________________________( )
2023 г.
СОДЕРЖАНИЕ
I. Введение………………………………………………………………………....3
II. Основная часть……………………………………………………………..…..4
2.1 История развития фрактальной геометрии…………………………….……4
2.2 Понятие фрактала………………………………………....…………………..5
2.3 Виды фракталов………………………………………………………….……6
2.4 Практическое применение фракталов……………………………………...9
2.5 Создание собственных фракталов (модели )………………………………11
III. Заключение. ………………………………………………………………….13
Выводы……………………………………………………………………….…..14
Используемая литература………………………………………….……………15
-
Введение.
Геометрию часто называют холодной и сухой. Одна из причин заключается в ее неспособности описать все то, что окружает нас: форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой. С огромной для нас радостью мы узнали, что в современном мире существует новая геометрия – геометрия фракталов.
Открытие фракталов произвело революцию не только в геометрии, но и в физике, химии, биологии, во всех областях нашей жизни.


Актуальность данной работы:
Роль фракталов в современном мире важна. Они постоянно помогают учёным, инженерам, дизайнерам, компьютерщикам.
Объект исследования:
Человек, геометрические абстракции, изобретения созданные человеком, окружающий нас мир.
Предмет исследования:
Форма и строение исследуемых предметов и явлений.
Цель исследования:
Изготовление примера фрактала.
Поставленная цель предусматривает решение следующих задач:
- Изучить информацию о фракталах.
- Рассмотреть различные виды фракталов.
- Познакомиться с новым направлением в математике - Фрактальной геометрией.
- Узнать где возможно применение фракталов.
- Сделать пример своего фрактала доступными методами.
- Сделать необходимые выводы.
Гипотеза: Я предполагаю, что изучив всю информацию о фракталах, я смогу сделать модель фрактала.
Методы исследования: теоретический, экспериментальный, практический, анализ, обобщение.
Практическая и теоретическая значимость:
Использование приобретенных знаний и навыков исследовательской работы, для поддержки разговора, для компьютерной графики, для описания различных объектов с помощью фракталов. Использование материала на уроках и факультативных занятиях по математике и информатике. Эта тема уникальна и касается окружающего нас мира.
Продуктом исследования: является собственная модель фрактала.
II. Основная часть.
2.1 История развития фрактальной геометрии.
Проблема изучения самоподобных объектов, с необычными, с точки зрения классической математики свойствами, была рассмотрена еще в конце XIX – начале XX века в работах Жюлиа, Пуанкаре, Пеано, Кантора, Хаусдорфа и других известных ученых. Но именно Мандельброт был первым, кому удалось объединить разрозненные научные результаты и показать их практическую значимость.
Термин фрактал был впервые использован для описания самоподобных структур в работе франко-американского математика Бенуа Мандельброта "Фракталы" в 1975 году.
Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Бенуа Мандельброта "Фрактальная геометрия природы". Мандельброт положил начало систематическому изучению фракталов. Своими яркими и фундаментальными работами он пробудил всеобщий интерес к фрактальной геометрии.
История фракталов в XIX веке началось именно с изучения геометрических фракталов. Фракталы ярко отражают свойство самоподобия. Наиболее наглядными примерами геометрических фракталов являются:
*Кривая Коха — несамопересекающаяся непрерывная кривая бесконечной длины. Эта кривая не имеет касательной ни в одной точке.
*Губка Менгера — это аналог множества Кантора с тем лишь отличием, что построен этот фрактал в трехмерном пространстве.
*Треугольник или ковер Серпинского также является аналогом множества Кантора на плоскости.
*Фракталы Вейерштрасса и Ван дер Вардена представляют собой недифференцированную непрерывную функцию.
*Траектория броуновский частицы также не дифференцируема.
*Кривая Пеано — это непрерывная кривая, которая проходит через все точки квадрата.
*Дерево Пифагора.
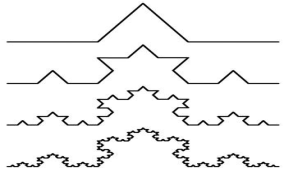
Рассмотрим триадную кривую Коха.
Для построение кривой существует простая рекурсивная процедура образования фрактала кривых на плоскости. В первую очередь необходимо задать произвольную ломаную с конечным числом звеньев, так называемым генератором. Далее каждое звено заменяется образующим элементом, точнее ломаной, подобной генератору. В результате такой замены образуется новое поколение кривой Коха. В первом поколении кривая состоит из четырех прямолинейных звеньев, длина каждого из которых равна 1/3. Чтобы получить третье поколение кривой выполняют тот же алгоритм — каждое звено заменяется на уменьшенный образующий элемент. Таким образом, для получения каждого последующего поколения, все звенья предыдущего заменяются уменьшенным образующим элементов. Тогда, кривая n-го поколения при любом конечном n называется предфракталом. В случае, когда n стремится к бесконечности кривая Коха становится фрактальным объектом.
Обратимся к другому способу построения фрактального объекта. Для его создания необходимо изменить правила построение: пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на образующий элемент таким образом, чтобы угол был сверху. То есть, при такой замене происходит смещение середины звена. Последующие поколения строятся по правилу: первое слева звено заменяется на образующий элемент таким образом, чтобы середина звена смещалась влево от направления движения. Далее замена звеньев чередуется. Предельная фрактальная кривая, построенная по такому правилу, называется драконом Хартера-Хейтуэя.
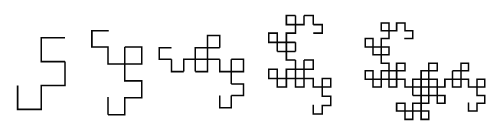
В компьютерной графике геометрические фракталы используются для моделирования изображений деревьев, кустов, горных массивов, береговой линии. Двухмерные геометрические фракталы широко используются для создания объемных текстур.
Бенуа́ Мандельбро́т (1924-2010) — французский и американский математик, создатель фрактальной геометрии. Лауреат премии Вольфа по физике (1993).

Бенуа Мандельброт родился в Варшаве в 1924 году. В 1936 году вся семья эмигрировала во Францию и поселилась в Париже. Здесь Мандельброт попал под влияние своего дяди Шолема Мандельбройта, известного парижского математика, члена группы математиков, известной под общим псевдонимом Николя Бурбаки.
У Бенуа открылся необычный математический дар, который позволил ему сразу после войны стать студентом Политехнической школы Парижа. Оказалось, что у Бенуа великолепное пространственное воображение. Даже алгебраические задачи он решал геометрическим способом. Оригинальность его решений позволила ему поступить в университет.
Окончив университет, Мандельброт переехал в США, где окончил Калифорнийский технологический институт. По возвращении во Францию, он получил докторскую степень в Университете Парижа в 1952 году. В 1958 году Мандельброт окончательно поселился в США, где приступил к работе в научно-исследовательском центре IBM в Йорктауне. Он работал в области лингвистики, теории игр, экономики, аэронавтики, географии, физиологии, астрономии, физики.
2.2 Понятие фрактала.
Фракта́л (лат. fractus — дробленый) — термин, введённый Бенуа Мандельбротом в 1975 году. До сих пор нет строгого математического определения фрактальных множеств. Он смог обобщить и систематизировать «неприятные» множества и построить красивую и интуитивно понятную теорию. Он открыл удивительный мир фракталов, красота и глубина которых порой поражают воображение, вызывают восторг у ученых, художников, философов. Работа Мандельброта была стимулирована передовыми компьютерными технологиями, которые позволили генерировать, визуализировать и исследовать различные множества.


Термин «фрактал» не является математическим понятием и в связи с этим не имеет строгого общепринятого математического определения. Более того, термин фрактал употребляется относительно любых фигур, обладающих какими-либо из нижеперечисленных свойств:
Нетривиальная структура на всех шкалах. Это свойство отличает фракталы таких регулярных фигур, как окружность, эллипс, график гладкой функции и т.п.
Увеличение масштаба фрактала не приводит к упрощению его структуры, то есть на всех шкалах мы увидим одинаково сложную картину, в то время, как при рассмотрении регулярной фигуры в крупном масштабе, она становится подобна фрагменту прямой.
Самоподобие или приближенное самоподобие.
Метрическая или дробная метрическая размеренность, значительно превосходящая топологическую.
Построение возможно лишь с помощью рекурсивной процедуры, то есть определение объекта или действия через себя.
Фрактал - геометрическая фигура, составленная из нескольких частей, каждая из которых подобна всей фигуре целиком. Небольшая часть фрактала содержит информацию обо всем фрактале. Сегодня под словом «фрактал» чаще всего принято подразумевать графическое изображение структуры, которое в более крупном масштабе подобно себе.
Центральной идеей фрактальной концепции является самоподобие как природных феноменов, так и социокультурных явлений, динамика которых раньше считалась хаотической. Самоподобие означает, что в рамках системы некоторые ее участки разного масштаба повторяют конфигурацию системы в целом, т. е. в пределах общей формы заключен бесконечно «тиражируемый» фрактальный паттерн.
2.3 Виды фракталов.
Фракталы можно разделить на регулярные и нерегулярные. Первые являются математической абстракцией, то есть плодом воображения. К примеру, снежинка Коха или треугольник Серпинского. Вторая разновидность фракталов является результатом природных сил или деятельности человека. Нерегулярные фракталы, в отличие от регулярных сохраняют способность к самоподобию в ограниченных пределах.
Любая часть фрактала содержит его уменьшенное изображение. То есть, сколько фрактал не увеличивай, из любой его части на нас будет смотреть его маленькая копия.