Добавлен: 26.10.2023
Просмотров: 88
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Фракталы делятся на группы. Самые большие группы это:
-
геометрические фракталы; -
алгебраические фракталы; -
системы итерируемых функций; -
стохастические фракталы.
-
Геометрические фракталы
Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Обычно при построении этих фракталов поступают так: берется "затравка" - аксиома - набор отрезков, на основании которых будет строиться фрактал. Далее к этой "затравке" применяют набор правил, который преобразует ее в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если мы проведем (по крайней мере, в уме) бесконечное количество преобразований - получим геометрический фрактал.
Классические примеры геометрических фракталов - Снежинка Коха, Лист, Треугольник Серпинского).
В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности объекта) Примерами таких кривых служат:
кривая дракона; кривая Коха; кривая Леви; кривая Минковского; кривая Пеано.
К геометрическим фракталам также относят фракталы, получаемые похожими процедурами, например: множество Кантора; треугольник Серпинского; коврик Серпинского; кладбище Серпинского; губка Менгера; дерево Пифагора.
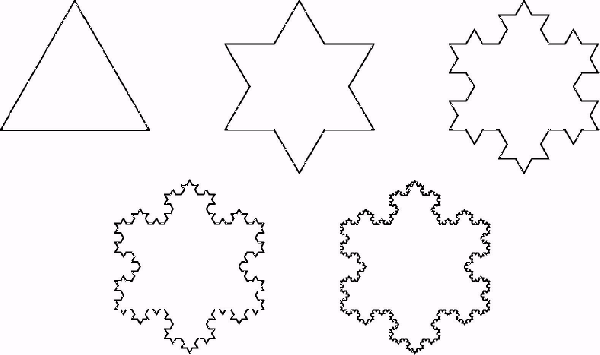
*Снежинка Коха.
Изобретена в 1904 году, немецким математиком Хельге фон Кохом.
Для ее построения берется единичный отрезок, делится на три равные части и среднее звено заменяется равносторонним треугольником без этого звена. На следующем шаге повторяем операцию для каждого из четырёх получившихся отрезков. В результате бесконечного повторения данной процедуры получается фрактальная кривая. *Пятиугольник Дюрера.
Фрактал выглядит как связка пятиугольников, сжатых вместе. Фактически он образован при использовании пятиугольника в качестве инициатора и равнобедренных треугольников, отношение большей стороны к меньшей в которых в точности равно так называемой золотой пропорции. Эти треугольники вырезаются из середины каждого пятиугольника, в результате чего получается фигура, похожая на 5 маленьких пятиугольников, приклеенных к одному большому.
*Треугольник Серпинского.
В 1915 году польский математик Вацлав Серпинский придумал занимательный объект.
Для его построения берется сплошной равносторонний треугольник. На первом шаге из центра удаляется перевернутый равносторонний треугольник. На втором шаге удаляется три перевернутых треугольника из трех оставшихся треугольников и т.д


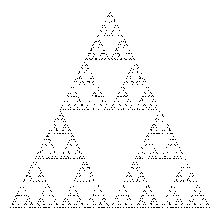

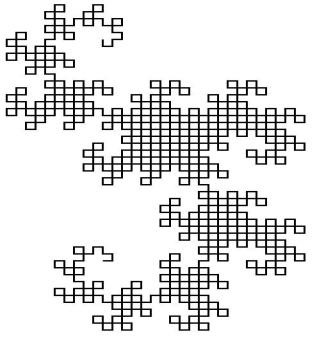
*Кривая Дракона.
Изобретена итальянским математиком Джузеппе Пеано.
Для его построения возьмем отрезок. Повернем его на 90 градусов вокруг одной из вершин и добавим полученный отрезок к исходному. Получим уголок из двух отрезков. Повторим описанную процедуру. Повернем уголок на 90 градусов вокруг вершины и добавим полученную ломаную к исходной.
Повторяя названные действия и уменьшая ломаные, будем получать все более сложные линии, напоминающие фигуру дракона.

*Ковер Серпинского.
Берется квадрат, разбивается на девять равных квадратов, средний из которых выбрасывается, а с остальными повторяется та же операция до бесконечности.


-
Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится - на экран выводится точка. При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:
С течением времени стремится к бесконечности.
Стремится к 0
Принимает несколько фиксированных значений и не выходит за их пределы.
Поведение хаотично, без каких либо тенденций.
Чтобы проиллюстрировать алгебраические фракталы обратимся к классике - множеству Мандельброта.
Для его построения нам необходимы комплексные числа. Комплексное число - это число, состоящее из двух частей - действительной и мнимой, и обозначается оно a+bi. Действительная часть a это обычное число в нашем представлении, а вот мнимая часть bi интересней. i - называют мнимой единицей. Почему мнимой? А потому, что если мы возведем i в квадрат, то получим -1.
Примеры алгебраических фракталов: множество Мандельброта; множество Жюлиа; бассейны Ньютона; биоморфы.
*Множество Мандельброта.
Множества Мандельброта наиболее распространенный среди алгебраических фракталов. Его можно найти во многих научных журналах, обложках книг, открытках, и в компьютерных хранителях экрана. Этот фрактал, напоминающий чесальную машину с прикрепленными к ней пылающими древовидными и круговыми областями.
*Множество Жюлиа.
Множество Жюлиа было изобретено французским математиком Гастоном Жулиа. Не менее известный алгебраический фрактал.
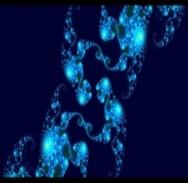
*Бассейны Ньютона.
Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости (для функции действительной переменной
метод Ньютона часто называют методом касательных, который, в данном
случае, обобщается для комплексной плоскости).




*Биоморфы.
(от греч. bios - жизнь и morphe - форма), феноиды (Negri, 1954) - жизненные формы, определяемые систематическим положением видов, их
формами роста и биологическими ритмами. К особым группам биоморф
относятся, например, лишайники, мхи, хвощи, плауны, папоротники.
Основными биоморфами среди высших растений являются деревья,
кустарники, кустарнички, полукустарники и полукустарнички, полутравы и травы.

-
Стохастические фракталы
Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в итерационном процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.
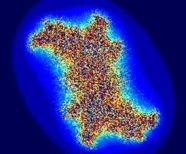
Типичный представитель данного класса фракталов "Плазма". Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок. Если мы теперь скажем, что цвет точки это высота над уровнем моря - получим вместо плазмы - горный массив. Именно на этом принципе моделируются горы в большинстве программ. С помощью алгоритма, похожего на плазму строится карта высот, к ней применяются различные фильтры, накладываем текстуру и пожалуйста фотореалистичные горы готовы.

2.4 Практическое применение фракталов
После открытия теории фракталов Бенуа Мандельбротом стало понятно, что данная теория может очень точно описывать многие явления в окружающем мире. Фрактальная теория и фрактальные алгоритмы сразу же нашли широкое практическое применение в различных областях науки и техники.
Фрактальное сжатие изображений. В 1990 и 1991 годах Майклом Барнсли и Аланом Слоуном была запатентована идея фрактальной архивации. Фрактальное сжатие изображений — алгоритм сжатия изображений с потерями, основанный на применении
систем итерируемых функций к изображениям. (Системы итерируемых функций или просто СИФ - представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое.) Данный алгоритм известен тем, что в некоторых случаях позволяет получить очень высокие коэффициенты сжатия (лучшие примеры — до 1000 раз (при приемлемом визуальном качестве) для реальных фотографий природных объектов, что недоступно для других алгоритмов сжатия изображений в принципе. Самые известные изображения, полученные с использованием СИФ – это Папоротник Барнсли (приложение 5) и Треугольник Серпинского(приложение 3). В настоящее время исследования в этой области продолжаются. Цель- как за меньшее время архивации получить качественное архивируемое изображение.
Фракталы в медицине. Человеческий организм состоит из множества фракталоподобных органов. Это прежде всего бронхи, легкие, кровеносные сосуды, мышцы.(приложение 5).
Так, кровеносные сосуды, многократно делясь и разветвляясь, пронизывая все органы, отражают свою фрактальную природу и имеют общую длину около 100 тыс. км. В первую очередь, фрактальные алгоритмы стали использовать при изучении электрокардиограмм, потому что электрическая активность сердца может быть описана как фрактальный процесс.
Легкие имеют пористую структуру, уникальную тем, что их огромная площадь размещена в очень маленьком пространстве: в среднем общая площадь внутренней поверхности альвеол в моменты выдоха и вдоха изменяется от 40 до 120 м2, само же количество альвеол у взрослого человека достигает порядка 700 млн. Точное описание структуры легких возможно с помощью фрактального изображения.
В настоящее время также ведутся медицинские исследования фрактальной структуры остеопороза- дегенеративного заболевания костной ткани. Возможно, это позволит прервать развитие болезни на начальном этапе. Исследования ведутся и в области рентгеновских изображений, в электрогастроэнтерографии, в офтальмологии и т.д.
Фракталы в музыкепоявились при помощи компьютера. Каждой точке и цвету множества дается определенное музыкальное значения- так создаются мелодии различных множеств.
Фракталы в радиоэлектронике, точнее говоря в конструкции антенн. Радиолюбитель Натан Коэн после посещения лекций Б. Мандельброта стал экспериментировать с формами и размерами антенн, чтобы получить антенну с высокой чувствительностью при маленьких размерах. Опытным путем из обычной проволоки он создал антенну в форме кривой Коха, которая смогла покрывать широкий диапазон частот и была существенно меньше классической антенны. Коэн запатентовал изобретение и основал фирму по изготовлению фрактальных антенн. Технологии фрактальных антенн в настоящее время используются в сотовых телефонах.