Автономная некоммерческая организация высшего образования «МОСКОВСКИЙ МЕЖДУНАРОДНЫЙ УНИВЕРСИТЕТ»

Кафедра экономики и управления Форма обучения: заочная

ВЫПОЛНЕНИЕ

ПРАКТИЧЕСКИХ ЗАДАНИЙ

ПО ДИСЦИПЛИНЕ

Теория вероятностей и математическая статистика

Группа Во20М561
Студент

Хакимова Полина Владимировна


МОСКВА 2023
Задача1

Буквы, составляющие слово РАКЕТА, написаны по одной на шести карточках; карточки перемешаны и положены в пакет.

1.1.Чему равна вероятность того, что, вынимая четыре буквы, ПОЛУЧИМ слово РЕКА?
Количество событий = общему количеству букв = 6.

Из них благоприятных событий (подходящих букв) = 1.

Вероятность по формуле Лапласа:

Р = 1 / 6.

Вероятность, что вторая буква Е:

Р = 1/5 (из оставшихся 5ти букв 1 Е);

Вероятность того, что третья буква будет К:

Р = 1/4 (из оставшихся 4х букв 1 К);

Вероятность того, что четвертая буква будет А:

Р = 2/3 (из оставшихся 3х букв 2 А);

Вероятность взаимосвязанных событий, что поочередно вынуты буквы Р, Е, К, А:


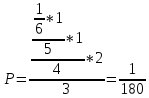
1.2.Какова вероятность сложить слово КАРЕТА при вынимании всех букв?
6 карточек: "ААЕКРТ". Берем первую карту. С вероятностью 1/6 вытащили "К". Осталось 5 карт "ААЕКТ". Берем вторую. С вероятностью 2/5 вытаскиваем "А". Осталось 4 карты "АЕКТ". С вероятностью 1/4 вытаскиваем "Р", потом с вероятностью 1/3 - "Е", 1/2 - "Т", 1 - "А".



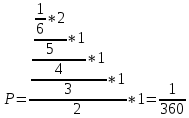
Задача 2
M = 4*0.4 + 6*0.1 + 10*0.2 + 12*0.3 = 7.8

D = 16*0.4 + 36*0.1 + 100*0.2 + 144*0.3 = 73.2

СКО = sqr(73.2) = 8.55

---

Задача3
Возможные значения дискретной случайной величины равны: -2, 1, 4. При

условии, что заданы математическое ожидание M( 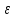) = 1.9, а также

M( 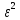) = 7.3, найти вероятности 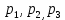, которые соответствуют

дискретным значениям случайной величины.

p₁+p₂+p₃=1
По определению математического ожидания
M[x]=x₁·p₁+x₂·p₂+x₃·p₃⇒
–2·p₁+p₂+4·p₃=1,9

M[x₂]=x21·p₁+x22·p₂+x23·p₃⇒
(–2)2·p₁+p₂+42·p₃=7,3
4·p₁+p₂+16·p₃=7,3

Решаем систему трех уравнений:

{p₁+p₂+p₃=1

{–2·p₁+p₂+4·p₃=1,9

{4·p₁+p₂+16·p₃=7,3


Упростим систему:
{p₁ + p₂ + p₃ = 1
{-20p₁ + 10p₂ + 40p₃ = 19
{40p₁ +10p₂ + 160p₃ = 73

Из первого уравнения выразим p₁ через остальные переменные
{p₁ = -p₂ – p₃ + 1
{-20p₁ + 10p₂ + 40p₃ = 19
{40p₁ +10p₂ + 160p₃ = 73

Во 2,3 уравнение подставим p₁
{p₁ = -p₂ – p₃ + 1
{-20(-p₂ – p₃ + 1) + 10p₂ + 40p₃ = 19
{40(-p₂ – p₃ + 1) +10p₂ + 160p₃ = 73

После упрощения получим
{p₁ = -p₂ – p₃ + 1
{30p₂ + 60p₃ = 39
{-30p₂ + 120p₃ = 33

Поделим второе уравнение на 30
{p₁ = -p₂ – p₃ + 1
{p₂ + 2p₃ = 1,3
{-30p₂ + 120p₃ = 33

Из 2 уравнения выразим p₂ через остальные переменные
{p₁ = -p₂ – p₃ + 1
{p₂ = -2p₃ + 1,3
{-30p₂ + 120p₃ = 33

В 3 уравнение подставим p₂
{p₁ = -p₂ – p₃ + 1
{p₂ = -2p₃ + 1,3
{-30(-2p₃ + 1,3 ) + 120p₃ = 33

После упрощения получим
{p₁ = -p₂ – p₃ + 1
{p₂ = -2p₃ + 1,3
{180p₃=72

Поделим 3 уравнение на 180
{p₁ = -p₂ – p₃ + 1
{p₂ = -2p₃ + 1,3
{p₃=0,4

Находим значения переменных p_1, p₂ с помощью p₃

О т в е т.

P₁=0,1

p₂=0,5

p₃=0,4

---

Смотрите также файлы

• Приложение б.docx

• Экологический риск.rtf

• Геометриялы оптика.docx

• Педагогті атыжні Сиитова ж кні 06. 09. 2022.docx

• Левченко Ирина Николаевна (15. 04. 192418. 01. 1973).docx