Файл: Контрольная работа по дисциплине Математическая логика и теория алгоритмов.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 26.10.2023
Просмотров: 178
Скачиваний: 9
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ
Федеральное государственное бюджетное образовательное учреждение высшего образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
КОНТРОЛЬНАЯ РАБОТА
по дисциплине «Математическая логика и теория алгоритмов»
Студент гр. з-442П12-5
М.Ю.Слесарева
Направления подготовки
09.03.03
«20» марта 2023 г.
Руководитель:
Ассистент каф. АСУ
Ст. преподаватель каф. АСУ
____________ А.В. Елецкая «____» ____________2023 г.
2023
Вариант 18
1. Проверить тождество A Δ (A Δ B) = B
Решение. Используя основные тождества алгебры множеств, преобразуем левую и правую часть к одному множеству.
Начнем с левой части.
A Δ (A Δ B) = (по определению Δ) (A \ (A Δ B)) ((A Δ B) \ A) =
= (A ¬ (A Δ B)) ((A Δ B) ¬A) = (по определению Δ) (A ¬ ((A ¬B)
(B ¬A))) (((A ¬B) (B ¬A)) ¬A). Преобразуем отдельно множества (A ¬ ((A ¬B) (B ¬A))) и (((A ¬B) (B ¬A)) ¬A).
a) (A ¬((A ¬B) (B ¬A))) = (закон де Моргана) (A (¬ (A ¬B)
¬ (B ¬A))) = ( по закону де Моргана) (A ((¬A ¬ ¬B) (¬B ¬ ¬A))) = = (A ((¬A B) (¬B A))) = A (¬A B) (¬B A) = (дважды применяя закон ассоциативности) A (¬B A) (¬A B) = A (A ¬B)
(¬A B) = (по закону поглощения) A (¬A B) = (по закону дистрибутивности) (A ¬A) (A B) = (так как подчёркнутое множество пустое) A B.
b) Аналогично преобразуя множество ((A ¬B) (B ¬A)) ¬A, получаем
((A ¬B) (B ¬A)) ¬A = (A ¬B ¬A) (B ¬A ¬A) =
= (A ¬A ¬B) (B ¬ A) = ( ¬B) (B ¬ A) = (B ¬ A) =
= B ¬ A
Таким образом, левая часть преобразована к множеству
(A B) (B ¬ A) =(B A) (B ¬ A) = B (A ¬ A)= B U = B.
Следовательно, тождество доказано.
2. Что можно сказать об истинностном значении высказывания p (¬r ¬q), если p (q r) имеет значение истина?
Решение. Так как ¬r ¬ q = ¬ ¬r ¬ q = r ¬ q = ¬ q r = q r, то
p (¬r ¬q) = p (q r) = И.
3. Переведите с естественного языка на язык логики предикатов:
Два целых числа могут делиться друг на друга, но не быть равными.
Решение. Универсум: Z = целые числа. Предикаты: x / y «x делится на y», x y «m не равно n». Формула:
x, y((x /y) (x y)).
4. Переведите с естественного языка на язык логики предикатов:
Не все студенты отличники или спортсмены.
Решение. Универсум: M = {люди}. Предикаты: C(x) «x студент» O(x) «x отличник», S(x) «x спортсмен». Формула:
x(С(x) & O(x) & S(x)).
5. Для бинарного отношения x ρ y ⇔ «x × y> 1», определенного на множестве R вещественных чисел, выясните, какими свойствами оно обладает (рефлексивность, симметричность, антисимметричность, транзитивность) и какими не обладает.
Решение. Отношение ρ не обладает рефлексивностью, так как, например, при x = 0 получим 0 ×0 = 0 <1.
Отношение ρ обладает симметричностью, так как для любых вещественных x, y из того, что x × y> 1 следует, что y ×x> 1 (по свойству симметричности умножения вещественных чисел).
Отношение ρ не является транзитивным, так как, например, при при x = 1, y = 4, z= 0,5 получим 1 ×4 = 4 > 1 и 4 ×0,5 = 2 > 1, но 1 ×0,5 = 0,5 < 1.
Таким образом, отношение ρ является симметричным и не является рефлексивным и транзитивным.
6. Пусть f отображение R в R. Рассмотрим отношение a ρ b ⇔ f(a) ≤ f(b). Приведите примеры таких отображений f, для которых отношение ρ является отношением частичного порядка, и примеры таких f, что ρ не является отношением частичного порядка.
Решение. При f(x) = x отношение ρ не симметрично, например, 1 ≤ 2, но 2 ≤ 1 не выполнено. Отношение является антисимметричным, поскольку
x ≤ y и y ≤ x влекут x = y. Отношение ρ, очевидно, является транзитивным, ибо если x ≤ y и y ≤ z, то x ≤ z. Таким образом, при f(x) = x отношение ρ является отношением частичного порядка.
При f(x) = 1 отношение ρ не является антисимметричным, поскольку, например, f(2)≤ f(3) и f(3) ≤ f(2) не влечёт 2 = 3. Таким образом, при f(x) = 1 отношение ρ не является отношением частичного порядка.
7. Используя математическую индукцию, докажите для целого n ≥ 1, что
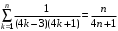.Решение. при n = 1,
, 
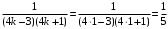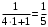.Для доказательства индуктивного перехода предположим, что для n = k выполнено
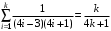. Имеем для n = k + 1: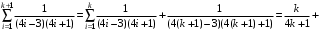 
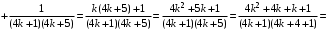
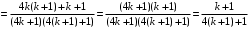. Что и требовалось доказать.8. Расположите следующие 5 функций в порядке увеличения скорости роста (каждая функция есть O (следующая)):
, 
, 
, 
, 
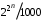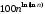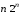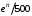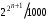.Решение. Так как любая экспонента растёт быстрее любой степенной функции, а любая степенная функция растёт быстрее любого логарифма, то наибольшую скорость роста имеют функции
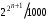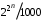и , причём, очевидно, что 
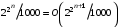. Далее, очевидно,
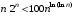, т.е. 
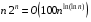и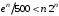 
, т.е. 
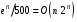.Таким образом,
, , 
,
.
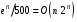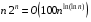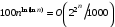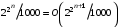