Лабораторная работа представляется к защите в виде отчета, содержащего постановку и решение задач линейного программирования, указанных в задании на работу.

Цель работы:

1. Построение математической модели реальных ситуаций в виде задачи ЛП.

2. Изучение возможностей пакетов прикладных программ для ЛП.

3. Решение индивидуальной задачи путем построения математической модели и использования пакета.

4. Анализ решений задачи ЛП.

Задание.

В аэропорту для перевозки пассажиров по n маршрутам может быть использовано m типов самолётов. Вместимость самолёта i-го типа равна a_i человек, а количество пассажиров, перевозимых по j-му маршруту за сезон, составляет b_i человек. Затраты, связанные с использованием самолёта i-го типа на j-ом маршруте, составляет c_ij руб.

Определить, сколько самолётов данного типа и на каком из маршрутов следует использовать, чтобы удовлетворить потребности в перевозках при наименьших общих затратах.

a₁ = 100; a₂ = 150; a₃ = 200; b₁ = 10 т; b₂ = 20 т; b₃ = 8 т; b₄ = 30 т

Таблица значений С:



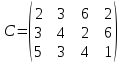
Подсчитать количество самолетов каждого типа в оптимальном решении. Как изменится решение, если самолетов 2-го типа есть только 100, а 3-го типа меньше 100.

Решение.

Математическая модель задачи в общем виде:

F = ∑∑c_ijx_ij, (1)

при условиях:

∑x_ij = a_i, i = 1,2,…, m, (2)

∑x_ij = b_j, j = 1,2,…, n, (3)

x_ij ≥ 0
Запишем экономико-математическую модель для нашей задачи.

Переменные:

x₁₁ – количество пассажиров, перевозимых самолетом 1-го типа по 1-му маршруту.

x₁₂ – количество пассажиров, перевозимых самолетом 1-го типа по 2-му маршруту.

x₁₃ – количество пассажиров, перевозимых самолетом 1-го типа по 3-му маршруту.

x₁₄ – количество пассажиров, перевозимых самолетом 1-го типа по 4-му маршруту.

x₂₁ – количество пассажиров, перевозимых самолетом 2-го типа по 1-му маршруту.

---

x₂₂ – количество пассажиров, перевозимых самолетом 2-го типа по 2-му маршруту.

x₂₃ – количество пассажиров, перевозимых самолетом 2-го типа по 3-му маршруту.

x₂₄ – количество пассажиров, перевозимых самолетом 2-го типа по 4-му маршруту.

x₃₁ – количество пассажиров, перевозимых самолетом 3-го типа по 1-му маршруту.

x₃₂ – количество пассажиров, перевозимых самолетом 3-го типа по 2-му маршруту.

x₃₃ – количество пассажиров, перевозимых самолетом 3-го типа по 3-му маршруту.

x₃₄ – количество пассажиров, перевозимых самолетом 3-го типа по 4-му маршруту.

Ограничения по количеству пассажиров, перевозимых за сезон:

100x₁₁ + 150x₂₁ + 200x₃₁ = 10000 (для 1-го маршрута)

100x₁₂ + 150x₂₂ + 200x₃₂ = 20000 (для 2-го маршрута)

100x₁₃ + 150x₂₃ + 200x₃₃ = 8000 (для 3-го маршрута)

100x₁₄ + 150x₂₄ + 200x₃₄ = 30000 (для 4-го маршрута)

Целевая функция – минимум затрат на перевозки:

2x₁₁ + 3x₁₂ + 6x₁₃ + 2x₁₄ + 3x₂₁ + 4x₂₂ + 2x₂₃ + 6x₂₄ + 5x₃₁ + 3x₃₂ + 4x₃₃ + x₃₄ → min

Затраты, связанные с использованием самолёта i-го типа на j-ом маршруте заданы матрицей тарифов.

	B1	B2	B3	B4
A1	2	3	6	2
A2	3	4	2	6
A3	5	3	4	1

---

Найдем решение задачи средствами Excel. Т.к. переменные по смыслу задачи могут принимать только целочисленные значения, то в ограничениях, задаваемых в диалоговом окне Поиск решения, необходимо указать, что переменные имеют целочисленные значения.

Вид электронной таблицы Excel, созданной для решения задачи, представлен на рис. Значения переменных x_ij располагаются в блоке ячеек B8:E10 (см. рис.).



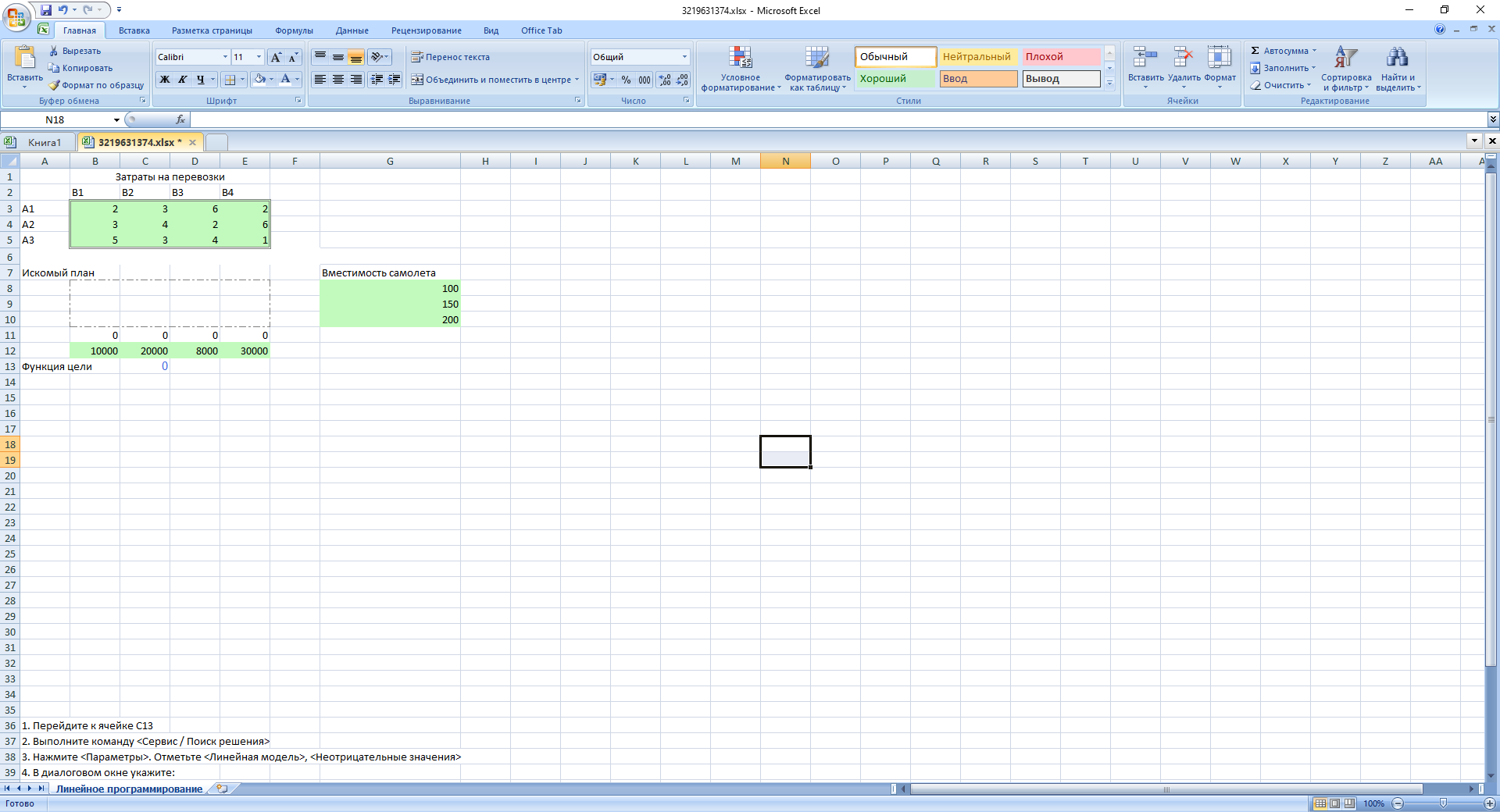
Коэффициенты целевой функции, отражающие расходы на перевозку находятся по адресам B3:E5. Данные о вместимости самолетов имеются в блоке G8:G10. Задан план перевозок - блоки B12:E12.

Формулы целевой функции и ограничений находятся соответственно в ячейке C13 и ячейках B11:E11 (ограничения по плану)

В группе Ограничения (см. рис. 3.16) заданы, помимо остальных, ограничения на целочисленность переменных (первая запись), означающие, что количество выбранных самолетов (значения x_ij) должно быть целым числом. Задание ограничения на целочисленность увеличивает время вычислений Поиска решения.



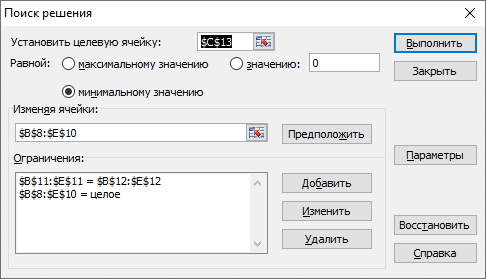
Результаты поиска решения приведены на рис. 3.14.



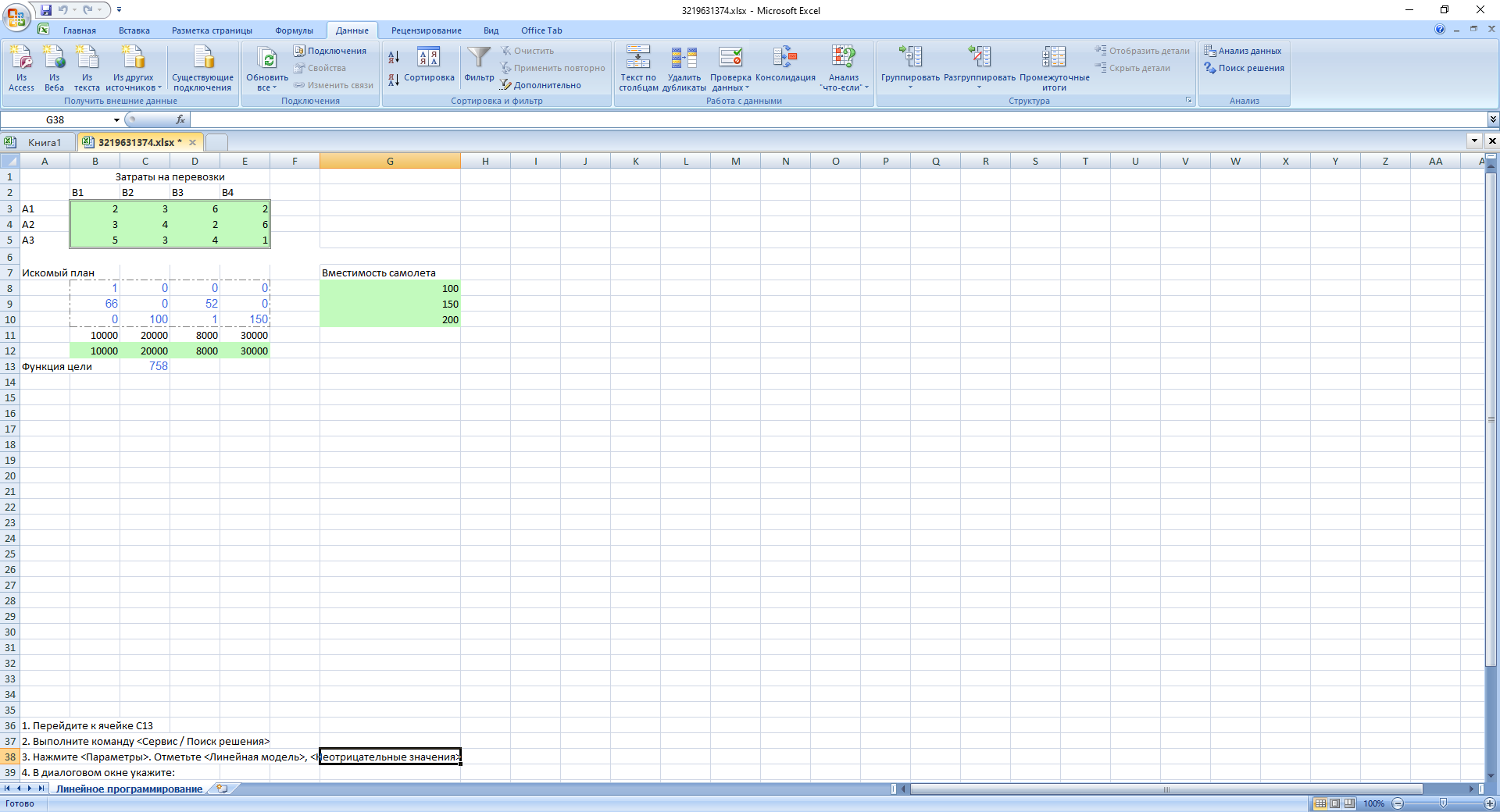
Решение задачи:

1 самолет 1-го типа направить по маршруту 1.

66 самолетов 2-го типа направить по маршруту 1 и 52 самолета 2-го типа направить по маршруту 3.

100 самолетов 3-го типа направить по маршруту 2, 1 самолет 3-го типа – по маршруту 3 и 150 самолета 3-го типа направить по маршруту 4.

Минимальные затраты составят:

F(x) = 1∙2 + 66∙3 + 100∙3 + 52∙2 + 1∙4 + 150∙1 = 758
Подсчитать количество самолетов каждого типа в оптимальном решении. Как изменится решение, если самолетов 2-го типа есть только 100, а 3-го типа меньше 100.

Добавим указанные ограничения в настройки Поиск решения:



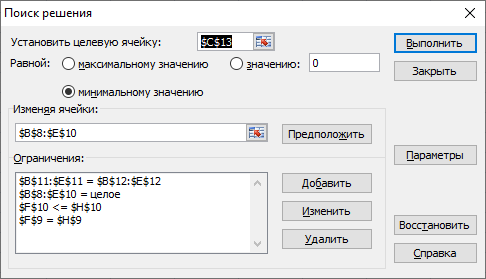
Получим:

Р
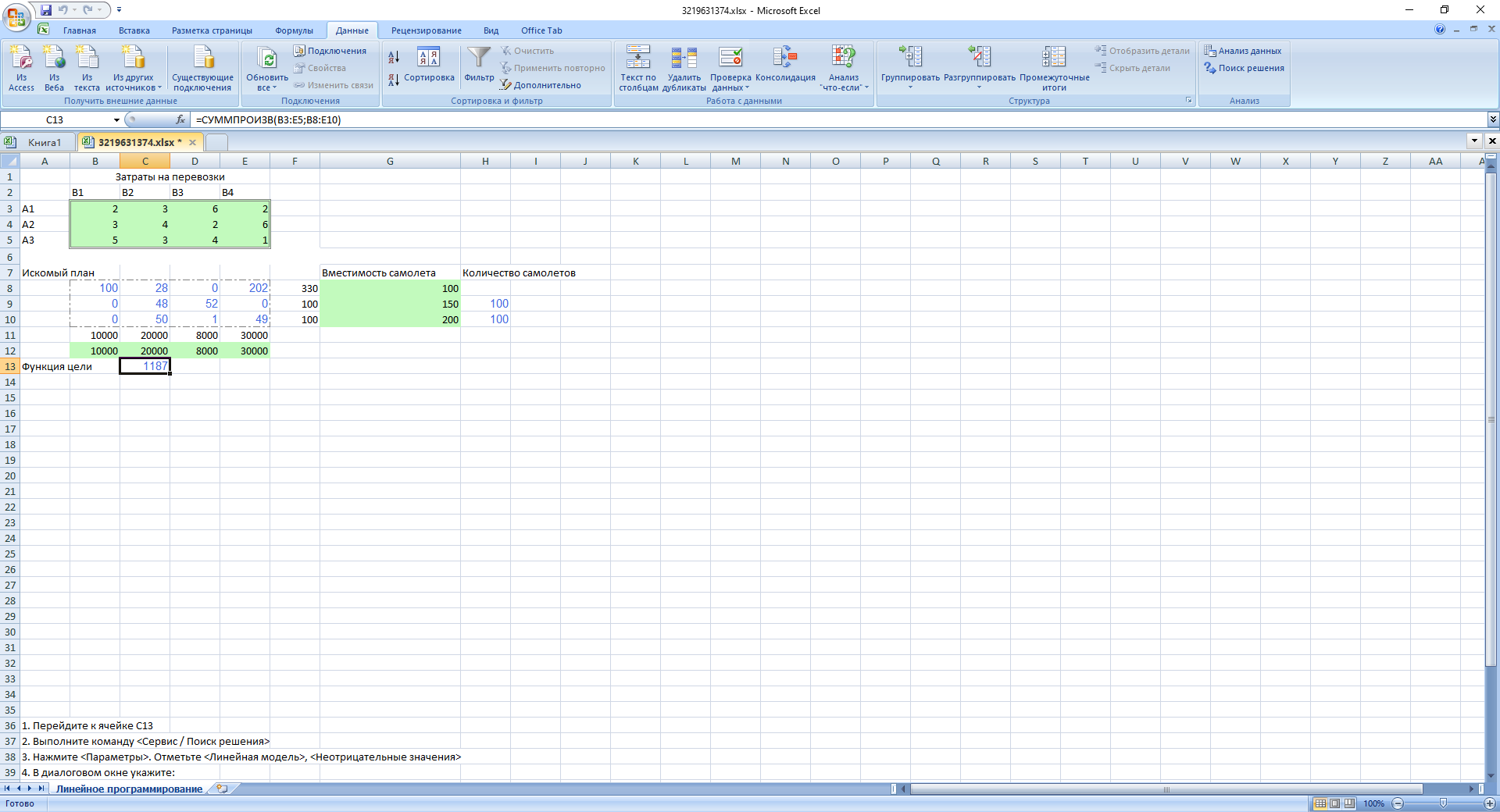
ешение задачи:

100 самолет 1-го типа направить по маршруту 1, 28 самолетов 1-го типа направить по маршруту 2 и 20 самолета 1-го типа направить по маршруту 4

48 самолетов 2-го типа направить по маршруту 2 и 52 самолета 2-го типа направить по маршруту 3.

---

50 самолетов 3-го типа направить по маршруту 2, 1 самолет 3-го типа – по маршруту 3 и 49 самолетов 3-го типа направить по маршруту 4.

Минимальные затраты составят:

F(x) = 100∙2 + 28∙3 + 202∙2 + 48∙4 + 52∙2 + 50∙3 + 1∙4 + 49∙1 = 1187

---

Смотрите также файлы

• Муниципальное бюджетное общеобразовательное учреждение г. Красноармейск Городского округа Пушкинский Московской области Средняя общеобразовательная школа 4.docx

• Приложение в глобализация в политике.docx

• Саба таырыбы Линзалар, линзаны оптикалы кшi, жа линзаны формуласы. Оу масаттары.docx

• Компьютер в жизни современного подростка.docx

• Незаконное проникновение в жилище особенности выявления и раскрытия.docx