1. 
   Дифференциальные уравнения движения материальной точки. Прямая и обратная задача динамики
   

Закон классической механики

1. 
   Если скорость тела равна 0 или постоянна, то равнодействующая сила рана 0
   
2. 
   Ускорение, получаемое телом, прямо пропорционально действующей силе и обратно пропорционально его массе. (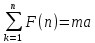
   

Дифференциальные уравнения движения материальной точки – составленные из 2-ого закона ньютона и есть дифф…

Для решения соответствующей задачи динамики необходимо составить уравнения, устанавливающие зависимость между массой движущей точки, ее ускорением и действующими на нее ускорениями. Дифференциальное уравнение движения точки в векторной форме и имеет вид: 

,  , - декартовой системы координат

,  . (2.3) - Если точка по криволинейной траектори, то используется Дифф… в естественной форме.

Задачи Динамики

1. 
   Прямая задача динамики: по кинематическому характеру движения материальной точки определить силу (силы), вызывающую это движение. Или Просто определения равнодействующий силы.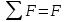 - равнодействиющий
   
2. 
   Обратная задача динамики: По заданной силе (силам), действующим на материальную точку (материальный объект) определить кинематические параметры её движения.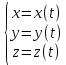 = =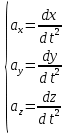ma=F
   

---

2. 
   Несвободное движение матер
   точки в естественных координатах
   

1. 
   Несвободное движение материальной точки – это такое движение вдоль кривой или поверхности, которое ограниченное какими-либо связями.
   

2. 
   Пусть материальная точка движется по гладкой поверхности, имеющей вид f (x;y;z) = 0
   

Следовательно, на точку действует: F –активная сила , N – нормальная реакция.

Основное уравнение динамики имеет вид : m*a = F+N

Проектируя на оси координат, получим дифференциальные уравнения движения 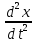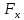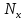m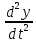 = 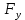+ 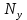, m = + , m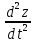 = 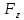+ 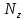. Из курса дифференциальной геометрии мы получим формулы :

Где

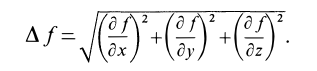
Таким образом, мы найдем нормальную реакцию N : ; ;

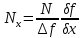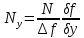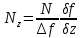
Обозначив   и подставив значения в основную формулу мы получим:




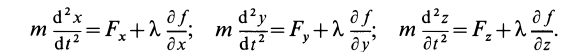
Эти дифференциальные уравнения называют дифференциальными уравнениями Лагранжа первого рода для движения несвободной материальной точки

3. 
   Относительное движение материальной точки. Уравнения покоя
   

---

Во многих задачах динамики движение материальной точки рассматривается относительно системы отсчета.

По 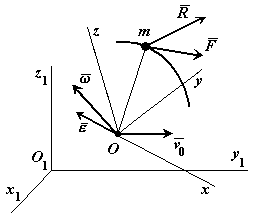лучим дифференциальные уравнения движения материальной точки относительно подвижной системы отсчета.

- инерциальная система отсчета.

- подвижная система отсчета.

,

где  - сумма активных сил, - сумма сил реакции связи.

Согласно теореме Кориолиса

Перепишем дифференциальное уравнение следующим образом



Материальная точка движется относительно неинерциальной системы отсчета так же как и относительно инерциальной, только к приложенным активным силам и силам реакции связей следует добавить кориолисову и переносную силу инерции.



Силы  и являются поправками на неинерционность системы.

Рассмотрим некоторые частные результаты.

1.   Пусть в подвижной СО –оси системы дижется равномерно, то   =0, так как в этом случае ω=0

(ω-угловая скорость вращения подвиж­ных осей Oxyz) и закон относительного движения принимает вид

---

 Σ  .

2. 
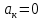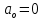   пусть , то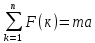
   

3 пусть 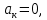то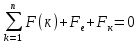

4.Теорема об изменении количества движения материальной точки.

Теорема: изменение количества движения материальной точки за некоторый промежуток времени равно импульсу приложенной к ней силы за тот же промежуток времени.

1. 
   Количество движения материальной точки находится как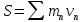 , следовательно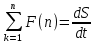
   
2. 
   В проектирования на оси: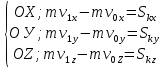
   
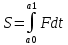
3. 
   
   

Частные случаи, следствия

• 
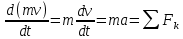
  При неупругом соударении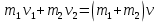
  
• 
  При упругом соударении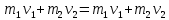
  
• 
  При реактивном движении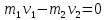
  

Над скоростью есть “_” знак вектороности.

5.Теорема об изменении кинетического момента.

Первая производная по времени от кинетического момента точки относительно какого-либо центра равна моменту силы относительно того же центра:

,

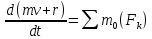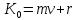
Проецируя на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента точки относительно этих осей координат:

---

,  ,

6 Момент инерции тела относительно оси. Теорема Гюйгенса-Штейнера.

,

Момент инерции тела определяется его размерами, формой, распределением и величиной массы, а также положением оси вращения.

Найдем связь между моментами инерции относительно двух различных параллельных осей. Она устанавливается теоремой Гюйгенса-Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции этого тела относительно оси проходящей через центр масс, параллельно данной и произведения массы на квадрат расстояния между осями.

Формула записывается во таким образом;



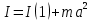
7. Теорема об изменении кинетической энергии для материальной точки.

Теорема: Изменение кинетической энергии материальной точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.

Полная работа на некотором конечном перемещении определяется интегралом: A=

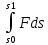
T=

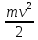
Пусть материальная точка M массы m движется под действием силы F из положения M₀ в положение M₁. Основываясь на основное уравнение динамики, которая имеет вид:  .

Заменим   и подставим в основное уравнение . Получим: .

---

Смотрите также файлы

• Кафедра теории и истории государства и права безопасность жизнедеятельности.doc

• 1. Виды контроля условий труда текущий контроль, целевые и комплексные проверки, аттестация рабочих мест. Контроль тяжелых, особо тяжелых, вредных и особо вредных условий труда.rtf

• Программа среднего профессионального образования 44. 02. 01 Дошкольное образование Дисциплина Практическое задание 1.docx

• Решением методического объединения 38. 02. 03 Операционная деятельность в логистике от 20 г. .docx

• Контрольная работа по дисциплине Основы научных исследований.docx