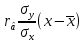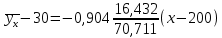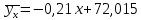Автономная некоммерческая образовательная организация высшего образования

«Сибирский институт бизнеса и информационных технологий»

Экзаменационная работа

№ 1 семестр

Дисциплина: Высшая математика


КЕЙС

Выполнил(а):

Мищенко Александр Владимирович

(Ф.И.О. студента)

Государственное и муниципальное управление

ГМНоз-1222(2)

(направление, группа)

Проверил(а):

_____________________________

(Ф.И.О. преподавателя)

18.06.2023

(дата)

Омск 2023 г.

Разработка практического задания на формирование УМЕНИЙ

Кейс-задание «Применение вероятностных методов для принятия экономических решений»

Задание 1. (Проверка параметрических гипотез)

Условие задачи.

Фирма предлагает автоматы по розливу напитков. При выборке n-16 найдена средняя величина х =182 г дозы, наливаемой в стакан автоматом №1. При выборке m-9 найдена средняя величина y =185 дозы, наливаемой в стакан автоматом №2. По утверждению изготовителя, случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсией , равной 25 22 σσ yх == . Можно ли считать отличия выборочных средних случайной ошибкой при уровне значимости α=0,01?

Поставлены задачи(ОПК-2, У3):

Решение:

Строим статистику и ={х_в -у_в)1^<У;1п + су1т ?

При выполнении гипотезы Н_о, т. е. а_х =а_у величина U

N(0,1). В условиях примера U_m61 - (185 - 182)/>/25/16 + 25/9 = -1,44. По заданному а=0,01 из таблицы функции Лапласа определим критические точки и,__я/2 = н_я_₂. Так как Ф(«₍₎₀₀₅) = 0,09/2, то Wo₀o5⁼2.57. Значение С_;иб = -1,44 не попадает в критическую область (-oo;-2,57)N(+2,57;+oo), поэтому Н„ принимается, следовательно, отличия выборочных средних - случайная ошибка.

Пусть Х Х(а_х, а_х), У И(а_у, о

---

_у), причем их дисперсии <т_л и о, неизвестны.

Выдвигается гипотеза о равенстве математических ожиданий:

Ну а_х=а_у, Ну а^а_у (Н^: а_х>а_у; Н^^2>: а_х<а_у).

При справедливости гипотезы Н_и статистика

Т = (х — у-) • у]пк(п + к -2)/(п + к) /^(п - 1)5² + (к -1)5² имеет t- распределение Стьюдента.
Задание 2. (Проверка гипотезы о распределении генеральной совокупности)

Условие задачи.

Масса (в граммах) 30 пачек полуфабоиката «Геркулес» такова:503,509,495,493,489,485,507,511,487,485,506,504,507,511,499,491,494,518,506,515, 487,509,507,488,495,490,498,497,492,495.

Поставлены задачи(ОПК-2, У3):

4) Построить статистический ряд распределения относительных частот;

5) Построить гистограмму выборочной оценки плотности вероятности;

6) Найти вывборочную среднюю и выборочную дисперсию по распределению выборки

7) Найти несмещунную оценку математического ожидания дисперсии

8) Найти доверительный интервал с надежностью 0,95 для оценки математического ожидания нормально распределенной случайной величины;

9-10) Проверить гипотезу о нормальном законе распределения случайной величины на уровне значимости α=0,05.

Решение.

Разобьем ряд на k 13.32lgn 13.32lg30  6 интервалов. Величина интервала

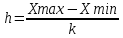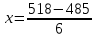=  6

Получим интервальный ряд:

Интервал	484;490	490;496	496;502	502;508	508;514	514;520
Середина интервал, zi	487	493	499	505	511	517
Ni	6	8	3	7	4	2
Wi	0.2	0.267	0.1	0.233	0.133	0.067

---

Найдем математическое ожидание:

M _z = 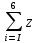_i * ω_i = 487*0.2+494*0.267+…+517*0.067=499.2;

Дисперсия D_z = 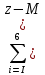_z )² ** ω_i =( 487-499.2)² *0.2+…+(517-499.2)² *0.067=87.56

F( 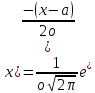, где а= М_z=499.2, σ =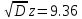

Найдем вероятности попадания случайной величины в интервалы.

P(484 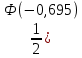= -Ф(-1,149)) =

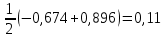= 1

Р(490 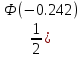= -Ф(-0.695)) =

=

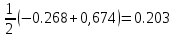
P(496 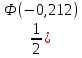= -Ф(-0,242)) =

=

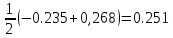
P(502 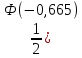= -Ф(-0,212)) =

=

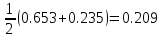
P(508 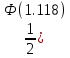= -Ф(0.665)) =

=

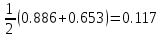
P(514 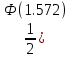= -Ф(-1.118)) =

=

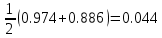
Найдем величину x² = n * 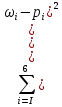= 30* ( +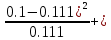

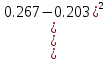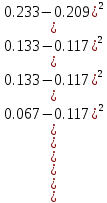+ ) = 5.969

Из таблицы возьмем значение ² _ar =² _0.05.3 =7.815, где   0.05 – уровень значимости, r  l t  63  3 – число степеней свободы ( l – число интервалов, t  3 – число условий). Т.к.   =² _0.05.3 , то гипотеза о нормальном распределении принимается.

Условие задачи (ОПК-2, У3):

---

С целью анализа взаимного влияния зарплаты и текучести рабочей силы на пяти однотипных фирмах с одинаковым числом работников проведены измерения уровня месячной зарплаты Х и числа уволившихся за год рабочих Y.

Поставлены задачи:

11) Построить поле корреляции

12) Найти выборочное уравнение линейной регрессии Y на Х

13) Найти выборочное уравнение линейной регрессии Х на Y

14) Найти выборочный коэффициент корреляции

15) Построить линии регрессии в поле корреляции.

Решение:

Линейная регрессия Y на X задается уравнением ӯ₂ –ӯ= r_xy *

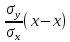
X	100	150	200	250	300
Y	60	35	20	20	15

Найти линейную регрессию Y на X, выборочный коэффициент корреляции.

Ищем выборочное среднее и выборочное среднее квадратическое отклонение

						Сумма
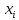	100	150	200	250	300	1000
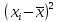	10000	2500	0	2500	10000	25000

Выборочная средняя

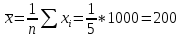
Выборочная дисперсия

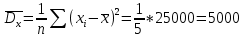
Выборочное квадратическое отклонение

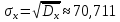
						Сумма
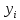	60	35	20	20	15	150
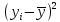	900	25	100	100	225	1350

---

Выборочная средняя

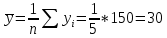
Выборочная дисперсия

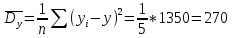
Выборочное квадратическое отклонение

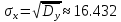
						Сумма
	100	150	200	250	300
	60	35	20	20	15
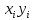	6000	5250	4000	5000	4500	24750

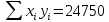
Коэффициент корреляции:



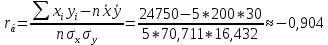
Уравнения регрессии:

=

---

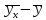Смотрите также файлы

• 5 "А" сыныбыны жылды бойынша ткізілген трбие жмыстарыны есебі.docx

• Устройство, обслуживание и настройка Электронного регулятора частоты вращения и мощности (эрчм) типа эрчм30Т.docx

• Порядок проведения разбора крупных, особо крупных пожаров. Документы разрабатываемые на проведение разбора пожара, порядок составления методического плана по разбору пожара.docx

• Практическая работа 29 на тему Электронные коллекции информационных и образовательных ресурсов, образовательные и специализированные порталы.docx

• Известия вузов России. Радиоэлектроника. 2010. Вып. 6 51 Полупроводниковая электроника, вакуумная и плазменная электроника.pdf