1 Выполнение задачи №1 «Сложение синусоидальных сигналов со сдвигом фаз. Теорема косинусов»

Для начала сформулируем необходимые для работы определения.

Сигнал- физический процесс, отображающий сообщение в удобной для передачи по каналу связи форме.

Фаза колебаний — аргумент периодической функции, {\displaystyle \sin(\omega t+\varphi _{0})} {\displaystyle \sin(\omega t+\beta x+\varphi _{0})}описывающей соответственно колебательный или волновой процесс.

Амплитуда колебаний — это наибольшее отклонение колеблющегося тела от положения равновесия.

Построим на оси времени две синусоиды и их суммирующую волну, при заданных значениях периода(T), времени(t) и фазы(ᵩ) (Рисунок1.2).

В рисунке 1.1 представим начальные параметры.

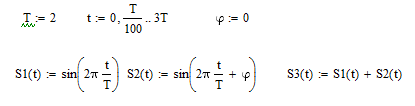
Рисунок 1.1-начальные параметры

---

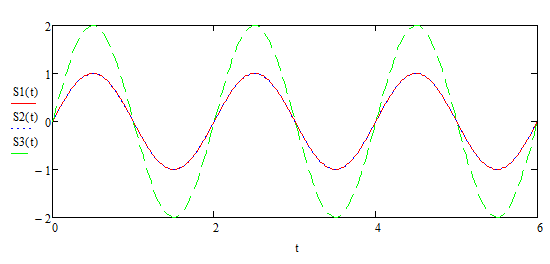
Рисунок 1.2 – две синусоиды и их суммирующая волна при фазе = 0

Заметим, что при фазе равной нулю амплитуда колебаний графика суммы двух синусоид равна 2 и что графики S1 и S2 принимают одинаковые значения (рисунок 1.2).

Теперь построим две синусоиды и их суммирующую волну, при этом изменив значение фазы на 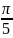(Рисунок 1.3).

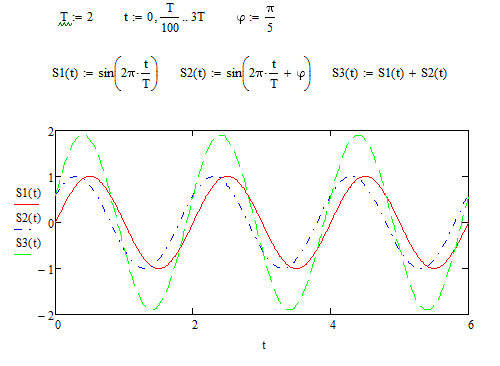
Рисунок 1.3 – две синусоиды и их суммирующая волна при фазе равной

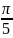
Заметим, что при фазе равной 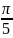амплитуда колебаний графика суммы двух синусоид равна 1.9 и что график S2 отстаёт от графика S1 из-за сдвига фаз(рисунок 1.3).

Сдвиг фаз- разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Теперь построим две синусоиды и их суммирующую волну, при этом изменив значение фазы на π (Рисунок 1.4).

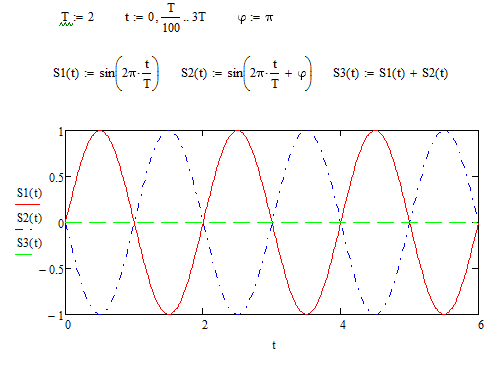
Рисунок 1.3 – две синусоиды и их суммирующая волна при фазе = π

Заметим, что при фазе равной π амплитуда колебаний графика суммы двух синусоид равна 0, так как графики S1 и S2 находятся в противофазе (рисунок 1.3).

Противофаза – момент совпадения максимума одного колебания с моментом минимума другого.

Поэтому при сложении таких графиков получаем ноль.

Теперь построим две синусоиды и их суммирующую волну, при этом изменив значение фазы на 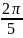(Рисунок 1.4) .

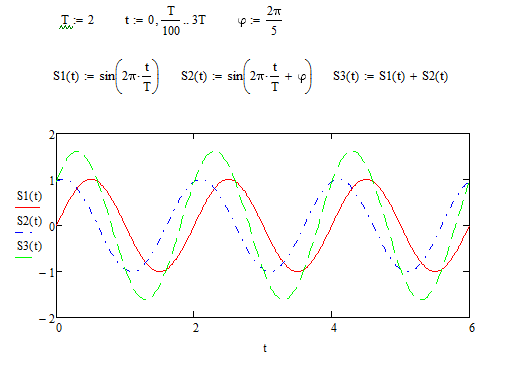
Рис. 1.4 – две синусоиды и их суммирующая волна при фазе

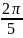
Заметим, что при фазе равной 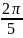амплитуда колебаний графика суммы двух синусоид равна 1.6 и что график S2 отстаёт от графика S1 из-за сдвига фаз(рисунок 1.4).

Теперь построим две синусоиды и их суммирующую волну, при этом изменив значение фазы на 2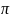 (рисунок 1.5).

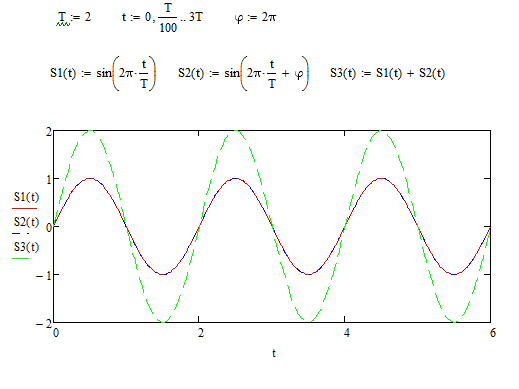
Рисунок 1.5 - две синусоиды и их суммирующая волна при фазе 2π

Заметим, что при фазе равной 2π амплитуда колебаний графика суммы двух синусоид равна 2 и что графики S1 и S2 принимают одинаковые значения (рисунок 1.5).

Вывод: при построении графиков я заметил закономерность, что при фазе [0;π] амплитуда графика суммы двух синусоид уменьшается, а при фазе [π;2π] увеличивается.

Правило параллелограмма- если два неколлинеарных вектора a и b привести к общему началу, то вектор с=а+b совпадает с диагональю параллелограмма, построенного на векторах a и b (рисунок 1.6). Причем начало вектора c совпадает с началом заданных векторов.

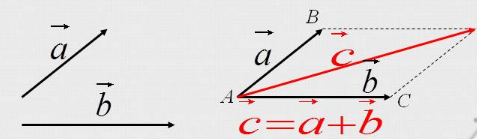
Рисунок 1.6 – правило параллелограмма

Для нахождения суммы векторов необходимо:

1. Отложить от точки A вектор АВ равный а и вектор АС равный b;

2. Достроить фигуру до параллелограмма и провести диагональ;

3. Диагональ параллелограмма- это сумма векторов.

Из правила параллелограмма следует теорема косинусов (рисунок 1.7):

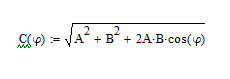
Рисунок 1.7- теорема косинусов

Где ᵩ-угол между A и B

А и В- складываемые векторы

Если взять вектора а и b равными 1, то получим выражение(Рисунок 1.10):

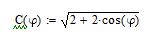
Рисунок 1.10- выражение, полученное из теоремы косинусов

В полярных координатах построим график зависимости длины результирующего вектора от угла ᵩ=0 . . 2π (Рисунок 1.11).

---

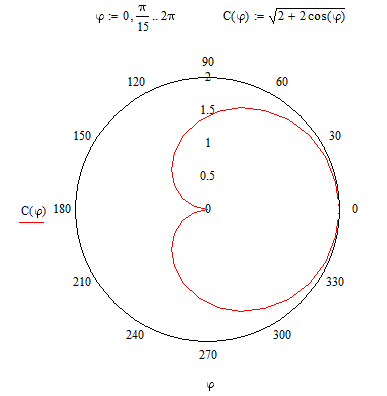
Рисунок 1.11 – график зависимости длины результирующего вектора от угла ᵩ=0 . . 2π

Теперь сравним длины результирующего вектора и амплитуды суммы двух гармонических функций S3(t) при одинаковых углах ᵩ (рисунок 1.12).

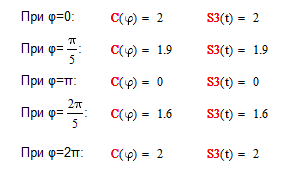
Рисунок 1.12- сравнение длины результирующего вектора и амплитуды суммы двух гармонических функций

Вывод: Длина результирующего вектора равна амплитуде суммы двух гармонических функций при одинаковых углах ᵩ

3. Выполнение задания №3 «Получение периодической последовательности прямоугольных импульсов суммированием гармоник. Построение амплитудного спектра»

Для начала нужно дать определения понятиям спектр сигнала и ширина спектра.

Спектр- это совокупность гармоник со строгим углом, фазой и частотой равной одной единице в сумме, которая и даёт сам сигнал.

Ширина — спектра это область частот, в пределах которой заключена основная часть энергии сигнала.

Выражение для гармоники разложения периодической последовательности прямоугольных импульсов в ряд Фурье:

,

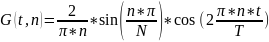где T-период последовательности импульсов; N- отношение периода к длительности импульса; n- номер гармоники.

Построим на оси времени графики первых трёх гармоник и их суммы (Рисунок 3.1):

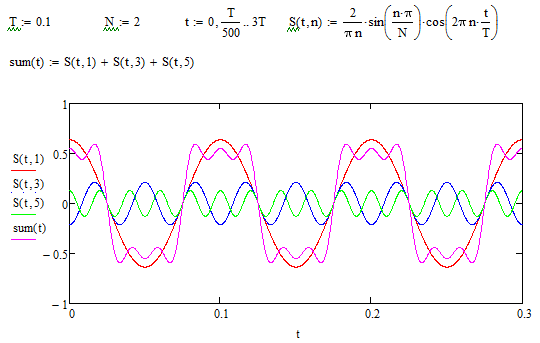
Рис. 3.1 – график трёх гармоник и их суммы

Берём гармоники только с нечётным номером, так как у чётных амплитуда равна нулю.

Теперь построим блок-схему для программы суммирования числа гармоник (Рисунок 3.2):

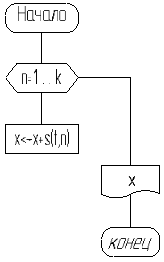
Рисунок 3.2 – блок-схема для программы суммирования числа гармоник

Далее напишем программу (Рисунок 3.3):

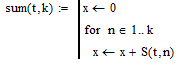
Рисунок 3.3- программа для суммирования числа гармоник

где k- количество гармоник.

Построим графики последовательностей, полученных при суммировании 5,10,100 гармоник.

При к=5 получим график (Рисунок 3.4):

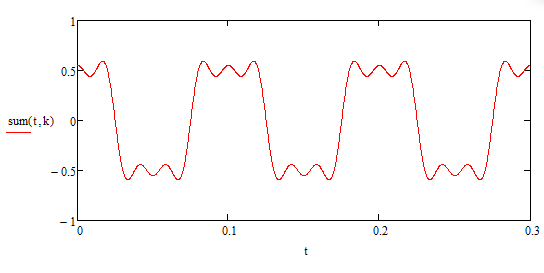
Рисунок 3.4 – график суммы 5 гармоник

При k=10 получим график (Рисунок 3.5):

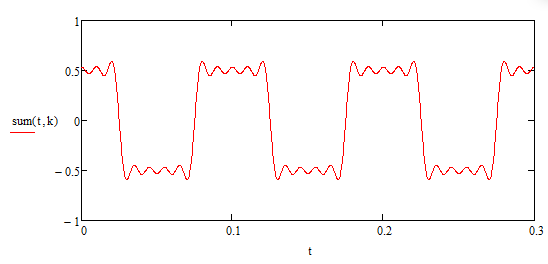
Рисунок 3.5 – график суммы 10 гармоник

При k=100 получим график (рисунок 3.6):

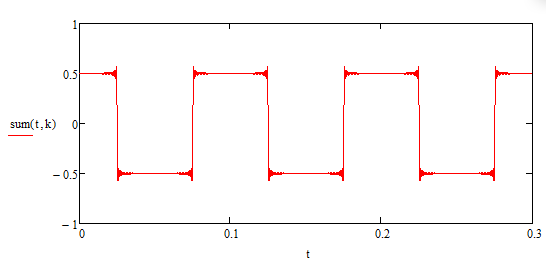
Рисунок 3.6 – график суммы при суммировании 100 гармоник

По графикам, изображённым выше можно понять, что последовательность из прямоугольных импульсов можно получить при помощи суммирования синусоид со всё более высокими частотами и всё более малыми амплитудами. И степень” прямоугольности” будет зависеть от количества суммируемых синусоид.

Построим амплитудный спектр последовательности в виде вертикальных, установленных в точках равных частоте гармоники (n/T), длина которых равна амплитуде соответствующей гармоники(Рисунок 3.7).

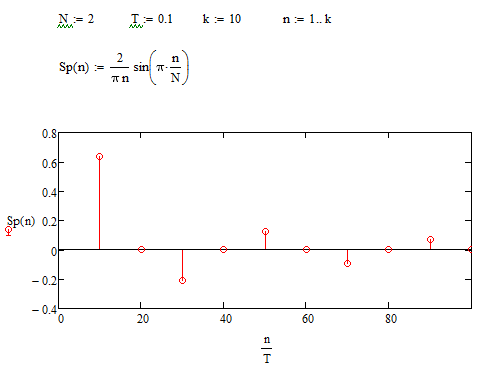
Рисунок 3.7 – амплитудный спектр

Построим графики спектров при постоянной длительности импульсов (Ƭ=0.1 ) и разной скважности N=2,4,10.

При N=2 график примет вид (Рисунок 3.8):

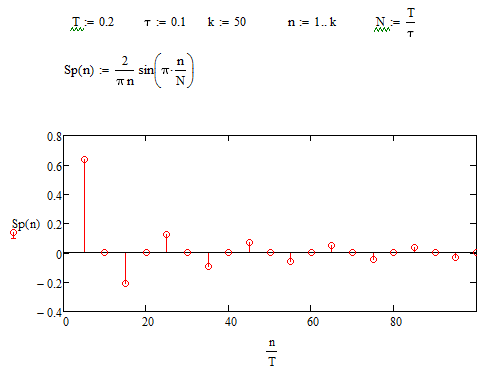
Рисунок 3.8 – график амплитудного спектра при N=2

При N=4 график примет вид (Рисунок 3.9):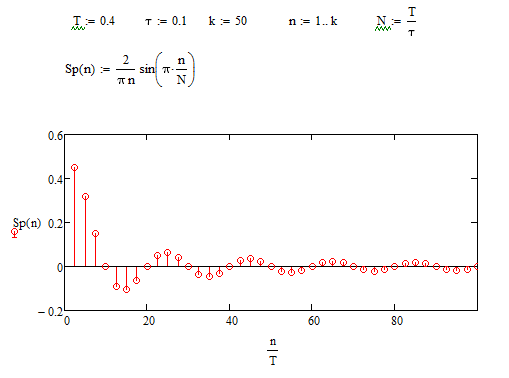

Рисунок 3.9 - график амплитудного спектра при N=4

При N=10 график примет вид (Рисунок 3.10):

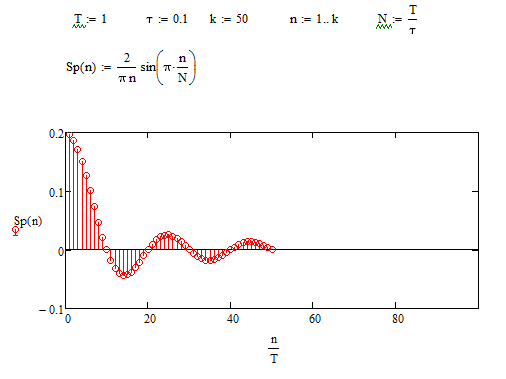
Рисунок 3.10 - график амплитудного спектра при N=10

---

Из графиков, представленных выше, можно сделать вывод: 1) При увеличении скважности уменьшаются амплитуды гармоник, спектральные линии становятся гуще. 2) Так как энергия сигнала оставаясь неизменной, перераспределяется между возросшим числом гармоник, то доля каждой гармоники в общем сигнале падает. 3) Количество гармоник в лепестке равно скважности.

Теперь построим графики спектров при одинаковой скважности (N=10) и разной длительности импульсов Ƭ = 0.1, 0.2, 1 секунд.

При Ƭ= 0.1 секунды получим график (Рисунок 3.11):

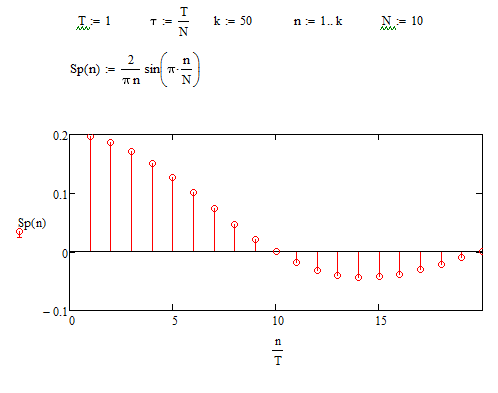
Рисунок 3.11 - график амплитудного спектра при Ƭ= 0.1 сек.

При Ƭ= 0.2 секунды получим график (Рисунок 3.12):

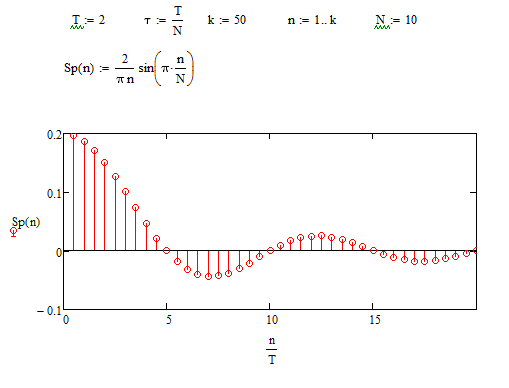
Рисунок 3.12 - график амплитудного спектра при Ƭ= 0.2 сек.

При Ƭ=1 секунде получим график (Рисунок 3.13):

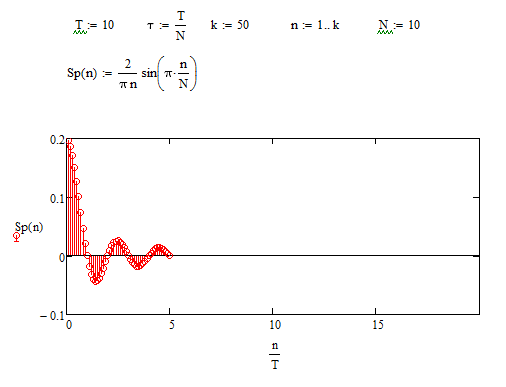
Рисунок 3.13 - график амплитудного спектра при Ƭ= 1 сек.

По этим трём графикам (рисунки 3.11, 3.12, 3.13) можно заметить, что ширина лепестка обратна пропорциональна длительности импульса.

Вывод: при переходе от периодического сигнала к непериодическому мы получаем в спектре такого сигнала вместо отдельных гармоник бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами, заполняющими всю шкалу частот. Причем амплитуда каждого такого колебания становится исчезающее малой, т.к. на его долю приходится бесконечно малая часть энергии сигнала.

---

4 Выполнение задания №4 «Генерация случайного двоичного массива и его визуализация на оси времени»

Для начала нам потребуется само определение массива.

Массив-структура данных в виде набора компонентов (элементов массива), расположенных в памяти непосредственно друг за другом.

Построим блок-схему генерации двоичного массива (Рисунок 4.1):

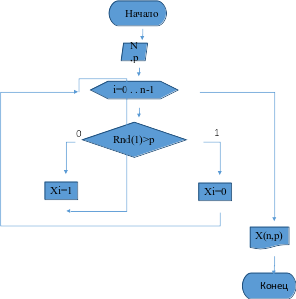
Рисунок 4.1 - блок-схема генерации двоичного массива

Теперь напишем программу генерации двоичного массива заданной длины с желаемой вероятностью появления единиц (Рисунок 4.2):

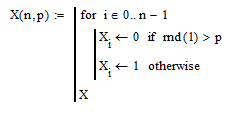
Рисунок 4.2 - программу генерации двоичного массива

n- количество элементов массива.

p- вероятность появления единиц.

Проверим частоту появления единиц в сгенерированных массивах при разных длинах массивов (10,100 и 1000 элементов) и одинаковой вероятности появления единиц (0.2):

При длине массива равной 10 элементам и вероятности появления единиц 0.2 получим (Рисунок 4.3):

Рисунок 4.3 – двоичный массив из 10 элементов

Частота появления единиц при заданных параметрах равна 0.2

Теперь изменим длину массива на 100 элементов (Рисунок 4.4):

Рисунок 4.4 – двоичный массив из 100 элементов

Частота появления единиц при заданных параметрах равна 0.26

Теперь изменим длину массива на 1000 элементов (Рисунок 4.5):

Рисунок 4.5 – двоичный массив из 1000 элементов

Частота появления единиц при заданных параметрах равна 0.204

Отсюда можно сделать вывод: при увеличении длины массива, увеличивается точность значения частоты появления единиц.

Повторим пункты 1 и 2 для массивов сгенерированных функцией rbinom.

Итак, сгенерируем двоичный массив длиной n=100 элементов и с вероятностью появления единиц p=0.2 (Рисунок 4.6):

Рисунок 4.6 - двоичный массив длиной n=100

Теперь проверим частоту появления единиц в массивах при разных длинах массивов (n=10,100 и 100 элементов) и при одинаковой вероятности появления единиц p=0.2 (Рисунок 4.7):

Рисунок 4.7 двоичный массив длиной n=10

Частота появления единиц при заданных параметрах равна 0.2

Изменим длину массива на 100 элементов (Рисунок 4.8):

Рисунок 4.8 - двоичный массив длиной n=100

Частота появления единиц при заданных параметрах равна 0.22

Изменим длину массива на 1000 элементов (Рисунок 4.9):

Рисунок 4.9 - двоичный массив длиной n=1000

Частота появления единиц при заданных параметрах равна 0.214

Визуализируем двоичный массив на оси времени (Рисунок 4.10):

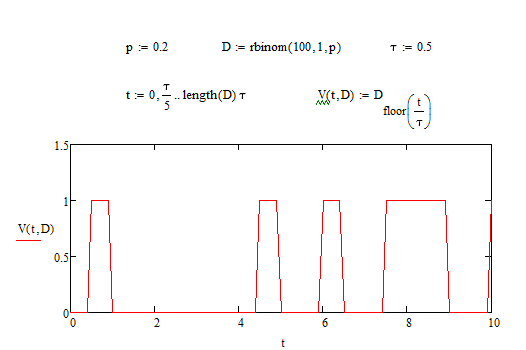
Рисунок 4.10 – двоичный массив на оси времени

Вывод: 1) Функция rbinom выполняет те же задачи, что и программа для генерации двоичного массива, а это значит: что гораздо рациональнее будет использование функции rbinom, ведь она более экономична и затрачивает меньше времени на написание. 2) При визуализации двоичного массива на оси времени, график принимает вид прямоугольного импульса.

5 Выполнение задания №5 «Моделирование АМ, ЧМ и ФМ модуляторов и наложение шума»

Для начала нужно разобраться что же такое модуляция и для чего она нужна?

---

Смотрите также файлы

• ВВС ОТВЕТЫ.docx

• Реферат Ятрогенная болезнь.docx

• Эпидемиология Населения.docx

• Экзамен10МБФ.doc

• экзамен микро.docx