Файл: Сложение синусоидальных сигналов со сдвигом фаз. Теорема косинусов.docx
Добавлен: 02.02.2019
Просмотров: 3373
Скачиваний: 57
Модуляция — процесс изменения одного или нескольких параметров высокочастотного (несущего) колебания по закону низкочастотного(информационного) сигнала.
Модуляция переносит спектр исходного сигнала на частоту несущей или в любую точку диапазона и зеркально отображает.
Сгенерируем случайный двоичный массив из 12 элементов с вероятностью единицы (p=0,5) (Рисунок 5.1):
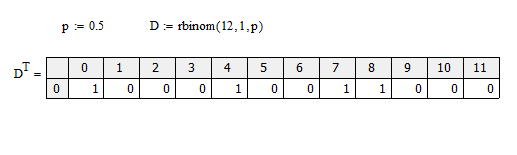
Рисунок 5.1 - двоичный массив из 12 элементов
Составим блок-схемы и напишем программы для амплитудной(AM), частотной(CM) и фазовой(FM) модуляций.
Начертим блок-схему для амплитудного модулятора (рисунок 5.2):
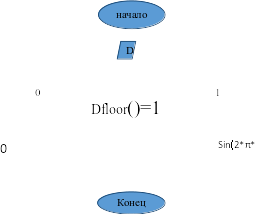
Рисунок 5.2 - блок-схема для амплитудного модулятора
А теперь напишем программу для амплитудного модулятора (Рисунок 5.3):
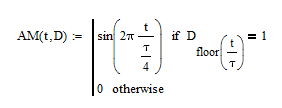
Рисунок 5.3 - программа для амплитудного модулятора
Начертим блок-схему для частотного модулятора (рисунок 5.4):
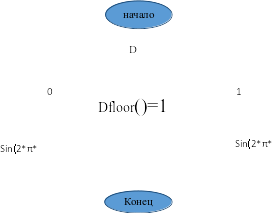
Рисунок 5.4 - блок-схема для частотного модулятора
А теперь напишем программу для частотного модулятора (Рисунок 5.5):
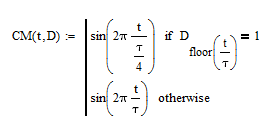
Рисунок 5.5 - программа для частотного модулятора
Начертим блок-схему для фазового модулятора (рисунок 5.6):
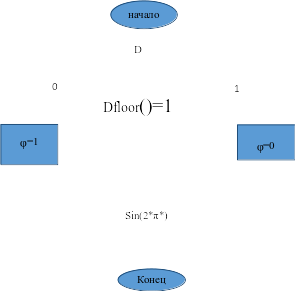
Рисунок 5.6 - блок-схема для фазового модулятора
А теперь напишем программу для фазового модулятора (Рисунок 5.7):
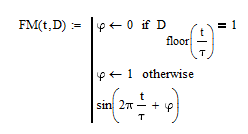
Рисунок 5.7 - программа для фазового модулятора
На графике времени выведем двоичный массив и модулированный сигнал для каждого вида модуляции при :
В рисунке 5.8 представим начальные параметры.
![]()
Рисунок 5.8- начальные параметры
Для амплитудной модуляции (рисунок 5.9):
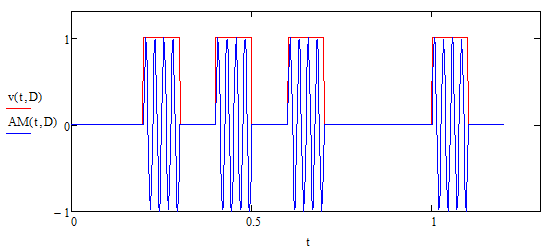
Рисунок 5.9 - двоичный массив и модулированный сигнал при амплитудной модуляции
Для частотной модуляции (рисунок 5.10):
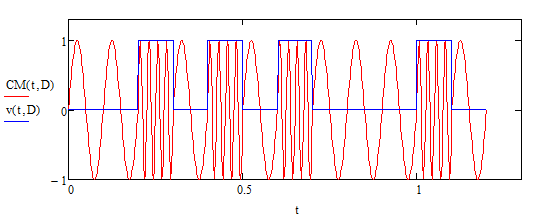
Рисунок 5.10 - двоичный массив и модулированный сигнал при частотной модуляции
Для фазовой модуляции (рисунок 5.11):
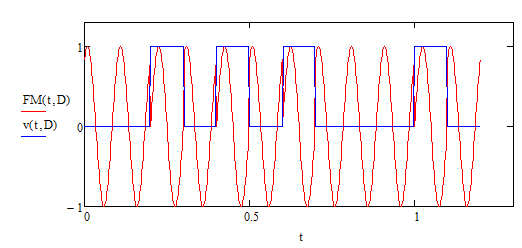
Рисунок 5.11 - двоичный массив и модулированный сигнал при фазовой модуляции
Далее нам понадобиться функция генерации случайной величины, распределённой по нормальному закону rnorm(L,m,ϭ).
rnorm(L,m,ϭ)-вектор L независимых случайных чисел, каждое из которых имеет нормальное распределение.
Нормальное распределение, также называемое распределением Гаусса-Лапласа- распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности.
Добавим к каждому отсчёту модулированного сигнала случайную величину генератора rnorm(1,0,ϭ) и выведем на графике.
ϭ – величина среднеквадратического отклонения шума.
Шум-беспорядочные колебания различной физической природы, отличающиеся сложностью временной и спектральной структуры.
Добавим шум к амплитудной модуляции (Рисунок 5.12):
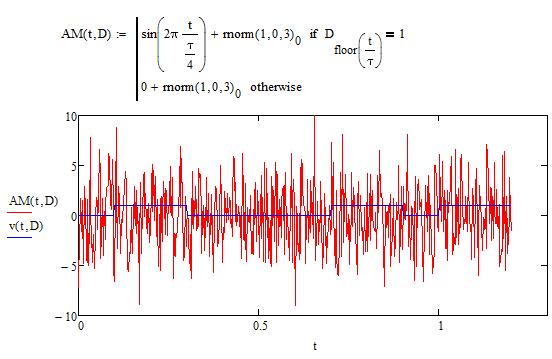
Рисунок 5.12 - двоичный массив и модулированный сигнал при амплитудной модуляции с шумом
Добавим шум к частотной модуляции (Рисунок 5.13):
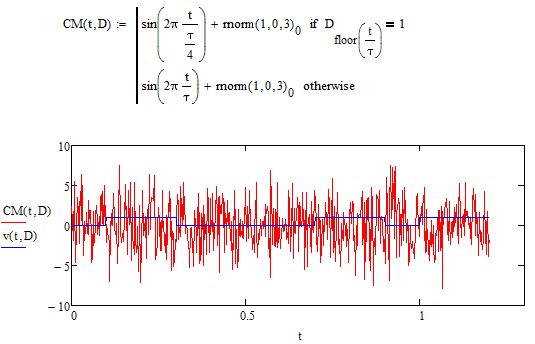
Рисунок 5.13 - двоичный массив и модулированный сигнал при частотной модуляции с шумом
Добавим шум к фазовой модуляции (Рисунок 5.14):
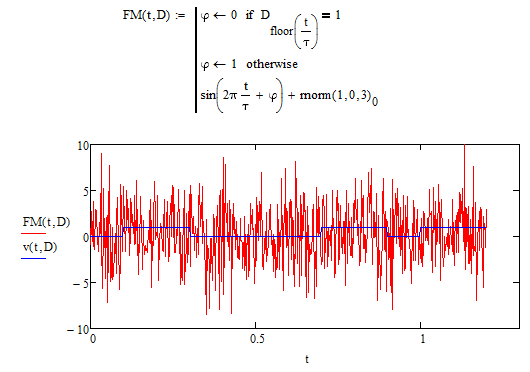
Рисунок 5.14 - двоичный массив и модулированный сигнал при фазовой модуляции с шумом
Вывод: Модуляция с шумом отображает условия, приближенные к реальным, ведь в обычной жизни передать сообщение без искажений невозможно, так как сществует огромное количество факторов создающих шум. Шум снижает качество передачи, так как сигнал в процессе искажается, а так же шум усложняет процесс приёма, потому что информационный сигнал гораздо сложнее выделить из модулированного колебания при присутствии шума.
6 Выполнение задания №6 «Применение многопозиционных сигналов»
Для определения скорости передачи информации используют формулу:
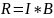
Где, I- количество информации приходящейся на один элемент, B- скорость модуляции.
Двоичные системы передачи имеют максимальную удельную скорость передачи 2 бит/с*Гц, которую иногда называют скоростью Найквиста. И тут возникает резонный вопрос, как же увеличить скорость? А сделать это можно за счёт использования многопозиционных сигналов, в этом случае один элемент линейного сигнала несёт информацию о большем числе символов данных, чем в двоичных системах. Но этот метод не идеален, так как при его использовании уменьшается помехоустойчивость.
Попробуем показать на примере как это работает, но для этого нам потребуется написать несколько программ.
Составим блок схему (Рисунок 6.1) и напишем программу преобразования двоичного числа в десятичное (Рисунок 6.2).
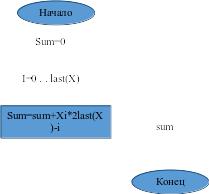
Рисунок 6.1 – блок-схема для программы преобразования двоичного числа в десятичное
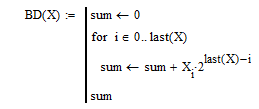
Рисунок 6.2 - программа преобразования двоичного числа в десятичное
Составим блок-схему (Рисунок 6.3) и напишем программу преобразования двоичного массива в массив десятичных элементов для заданного значения количества информации, приходящегося на один элемент(I) (Рисунок 6.4) .
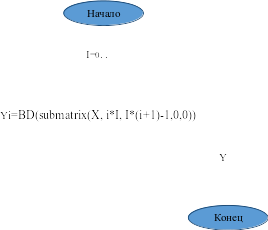
Рисунок 6.3 – блок-схема для программы преобразования двоичного массива в массив десятичных элементов
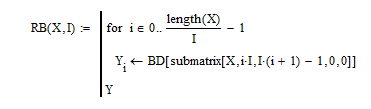
Рисунок 6.4 - программа преобразования двоичного массива в массив десятичных элементов
На одном графике визуализируем двоичный и десятичный массив при одинаковой длительности единичного элемента и при одинаковом времени передачи для (I=2,3,4).
На рисунке 6.5 представим начальные параметры.
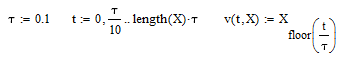
Рисунок 6.5- начальные параметры
При I=2 получим график (Рисунок 6.6):
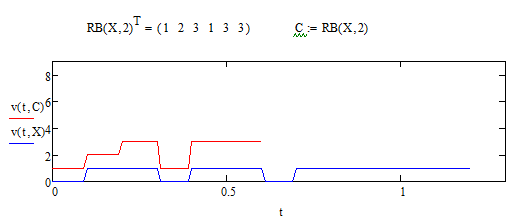
Рисунок 6.6 – график двоичного и десятичного массива при I=2
При I=3 получим график (Рисунок 6.7):
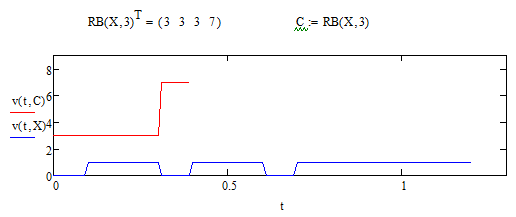
Рисунок 6.7 - график двоичного и десятичного массива при I=3
При I=4 получим график (Рисунок 6.8):
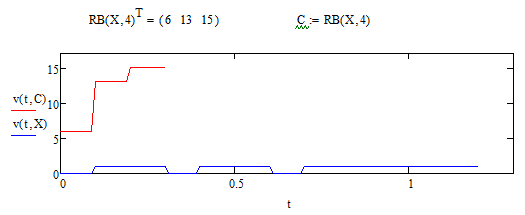
Рисунок 6.8 - график двоичного и десятичного массива при I=2
Вывод: При увеличении количества информации приходящейся на 1 элемент ‘I’ , продолжительность сигнала уменьшается, а значит увеличивается скорость передачи ‘R’.
Выровняем максимальные амплитуды двоичного и десятичного сигнала и добавим к каждому отсчёту сигнала случайную величину генератора rnorm(1,0, ϭ).
График двоичного сигнала, при rnorm(1,0,0.4), примет вид (Рисунок 6.9):
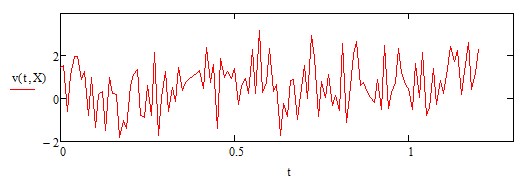
Рисунок 6.9 - График двоичного сигнала, при rnorm(1,0,0.4)
График десятичного сигнала, при rnorm(1,0,0.4) и при I=3, примет вид (Рисунок 6.10):
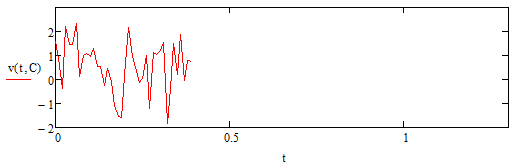
Рисунок 6.10 - График десятичного сигнала, при rnorm(1,0,0.4)
Вывод: При увеличении шума первоначальный сигнал становиться всё сложнее распознать, а значит шанс возникновения ошибок возрастает. И чем больше значение I, тем больше шанс возникновения ошибок.
Составим блок-схему (Рисунок 6.11) и напишем программу преобразования десятичного числа в двоичное (Рисунок 6.12) :
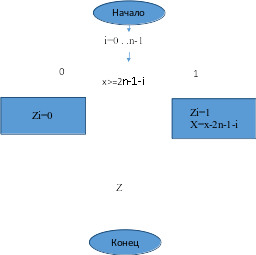
Рисунок 6.11 – блок-схема для программы преобразования десятичного числа в двоичное
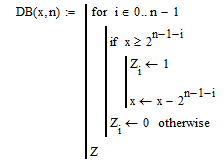
Рисунок 6.12 – программа преобразования десятичного числа в двоичное
Теперь составим блок-схему (Рисунок 6.13) и напишем программу преобразования десятичного массива в массив двоичных чисел (Рисунок 6.14):

Рисунок 6.13 – блок-схема для программы преобразования десятичного массива в массив двоичных чисел

Рисунок 6.14 – программа преобразования десятичного массива в массив двоичных чисел
Пример работы программы (Рисунок 6.15):
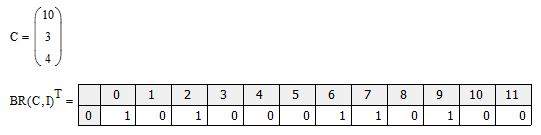
Рисунок 6.14 – массив десятичных чисел, преобразованный в массив двоичных
Здесь C- это десятичный массив, а BR- двоичный массив, преобразованный из десятичного.
Вывод: В данной работе мною было выявлено, что при увеличении количества информации приходящейся на 1 элемент ‘I’ , продолжительность сигнала уменьшается, а значит увеличивается скорость передачи ‘R’, но с увеличение значения I шанс возникновения ошибок возрастает и сигнал становиться малораспознаваемым. И получается что при применении многопозиционных сигналов платой за более высокую скорость является большая вероятность возникникновения ошибок.
7 Выполнение задания №7 «Шифрование текстового файла алгоритмом с симметричным ключом»
Шифрование — это преобразование данных в вид, недоступный для чтения без соответствующей информации (ключа шифрования).
Создадим текстовый файл при помощи блокнота, запишем в него текст «мама мыла раму» и сохраним его на диске в формате Юникод, назначив имя «shifr».
Далее считаем наш файл в MathCAD командой READBIN (Рисунок 7.1):
![]()
Рисунок 7.1 – применение команды READBIN
Теперь преобразуем десятичные значения байтов всех символов в единый двоичный массив. Для этого напишем программу перевода десятичного числа в двоичное (Рисунок 7.2) и программу перевода массива десятичных чисел в массив двоичных (Рисунок 7.3):
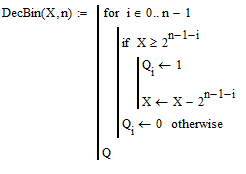
Рисунок 7.2 - программу перевода десятичного числа в двоичное
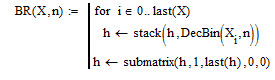
Рисунок 7.3 - программу перевода массива десятичных чисел в массив двоичных
Теперь, когда у нас есть двоичный массив, нужно создать ключ длиной 4 элемента и зашифровать им двоичную последовательность.
Ключ у нас будет вот такого вида (Рисунок 7.4):
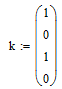
Рисунок 7.4 – ключ шифрования
Для того чтобы зашифровать двоичную последовательность нашим ключом, нужно создать программу, которая будет сравнивать каждые 4 элемента двоичного массива с ключом при помощи функции xor, которая работает по правилу (Рисунок 7.5):
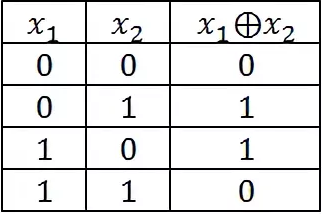
Рисунок 7.5 – таблица истинности для строгой дизъюнкции
И так, напишем программу, которая зашифрует двоичную последовательность (Рисунок 7.6):
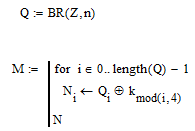
Рисунок 7.6 – программа шифрования двоичной последовательности
Теперь преобразуем зашифрованную двоичную последовательность в десятичные значения, учитывая формат представления (uint 16- два байта).
Для этого необходимо написать программу перевода двоичного числа в десятичное (Рисунок 7.7):
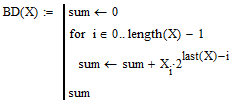
Рисунок 7.7 - программа перевода двоичного числа в десятичное
Далее напишем программу перевода массива двоичных чисел в массив десятичных (Рисунок 7.8):
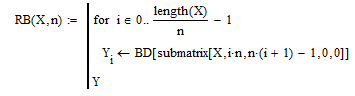
Рисунок 7.8 - программа перевода массива двоичных чисел в массив десятичных
Теперь, когда у нас есть десятичный массив, мы можем преобразовать вектор десятичных чисел в строковые символы командой vec2str (Рисунок 7.9):
![]()
Рисунок 7.9 – применение команды vec2str
Далее запишем зашифрованный файл на диск командой WRITEBIN (Рисунок 7.10):
![]()
Рисунок 7.10 – применение команды WRITEBIN
Откроем файл «secret», который мы записали на диск (Рисунок 7.11):

Рисунок 7.11 – открытый файл «secret»
Теперь расшифруем наше сообщение, для этого нужно повторить все те действия что мы делали до этого:
-
Считаем файл «secret» в Mathcad при помощи команды READBIN;
-
Преобразовываем десятичные значения байтов всех символов в единый двоичный массив;
-
Только теперь уже не шифруем, а расшифровываем двоичную последовательность, применив тот же ключ, которым мы шифровали;
-
Преобразовываем расшифрованную последовательность в десятичные значения, учитывая формат представления;
-
Преобразовываем вектор десятичных чисел в строковые символы командой vec2str (Рисунок 7.12).
![]()
Рисунок 7.12 – применение команды vec2str
И вот мы уже видим расшифрованное сообщение.
-
Осталось только записать расшифрованных файл на диск командой WRITEBIN (Рисунок 7.13):
![]()
Рисунок 7.13 – применение команды WRITEBIN
Откроем файл «nesecret» и посмотрим, что в нём написано (Рисунок 7.14):
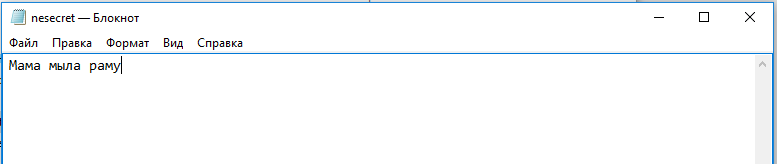
Рисунок 7.14 – открытый файл «nesecret»
А в нём храниться наше расшифрованное сообщение.
Вывод: в данной работе я обучился шифрованию текстового файла алгоритмом с симметричным ключом в среде Mathcad. Увидел как он работает на практике.