Файл: Лабораторная работа 3 Вариант 7 по дисциплине Метрология, стандартизация и сертификация 1.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 66
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство науки и высшего образования Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
«Национальный исследовательский Томский политехнический Университет»

Инженерная школа неразрушающего контроля и безопасности
20.03.01 Техносферная безопасность
Отделение автоматизации и робототехники
Косвенные однократные измерения
Лабораторная работа № 3
Вариант - 7
по дисциплине:
Метрология, стандартизация и сертификация 1.1
| Исполнитель: | | ||||
| студент группы | 1Е81 | | Цвингер А.А. | | 06.05.2021 |
| | | | | | |
| Руководитель: | Емельянова Е.Ю. | ||||
| преподаватель | | | | | |
| | | | | | |
Томск – 2021
Цель работы:
- освоение методов проведения однократных прямых и косвенных измерений;
- усвоение правил обработки, представления (записи) и интерпретации результатов проведенных измерений;
- приобретение практических навыков применения различных по точности средств измерений, а также анализа и сопоставления точности результатов косвенных измерений с точностью средств измерений, используемых при проведении прямых измерений;
- выявление возможных источников и причин методических погрешностей;
- закрепление теоретического материала по разделу «Метрология» изучаемой дисциплины «Метрология, стандартизация и сертификация».
Используемые технические средства:
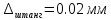 );
);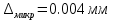 );
);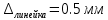
Ход работы
-
Проводим однократные измерения диаметра сечения и высоты цилиндров средствами измерений различной точности. Результаты измерений (без округления) записываем в таблицу 1:
Таблица 1 – Результаты измерений
| Измеряемый параметр | Деталь 1 (маленький) | Деталь 2 (большой) | ||
| Средство измерений | ||||
| штангенциркуль | микрометр | штангенциркуль | линейка | |
| Диаметр d, мм | 9,9 | 10 | 12,9 | 13 |
| Высота h, мм | 12,9 | 13 | 30,1 | 30 |
| Vизм., мм3 | 992,498265 | 1020,5 | 3932,018685 | 3979,95 |
| δv | 0,00718315 | 0,0027 | 0,00535758 | 0,0951821 |
| ΔV, мм3 | 7,129 | 2,75535 | 21,066 | 378,82 |
-
Определяем объем цилиндра по формуле (1), используя теоретическое соотношение, заносим в таблицу 1:
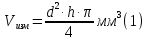
Деталь 1
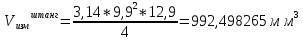
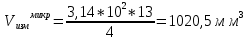
Деталь 2
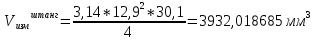
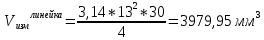
-
Определяем относительную погрешность, выраженную в относительных единицах, по формуле (2):
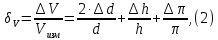
Деталь 1
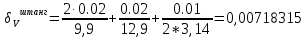
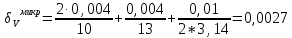
Деталь 2
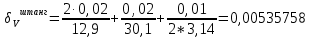
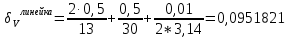
Предел допускаемой погрешности для π –
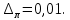
-
Определяем погрешность вычисления объема по формуле (3):
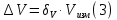
Деталь 1
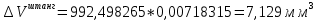
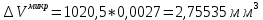
Деталь 2
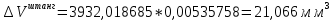
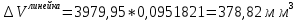
-
Запишем результат измерений объема цилиндра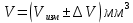
Деталь 1
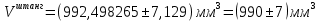
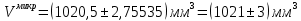
Деталь 2
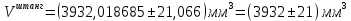
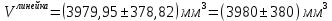
Вывод
В ходе лабораторной работы удалось освоить, закрепить и применить на практике теоретический материал по разделу «Косвенные однократные измерения».
Были получены навыки по правилам обработки, представления и интерпретации результатов проведенных измерений.
Удалось установить, что с помощью средства измерения с более высоким классом точности можно провести измерения точнее, чем на другом СИ с более низким классом точности. Доверительный интервал более точного средства измерения меньше доверительного интервала менее точного СИ.
Ответы на вопросы
-
Назовите основные виды измерений.
По числу измерений: однократное измерение
, многократное измерение.
По характеру точности (по условиям измерения): равноточные измерения, неравноточные измерения.
По выражению результата измерения: абсолютное измерение, относительное измерение.
По способу получения результата измерения: прямое измерение, косвенное измерение, совокупные измерения, совместные измерения.
По характеру измерения измеряемой физической величины: статическое измерение, динамическое измерение.
По метрологическому назначению используемых средств измерений: технические измерения, метрологические измерения.
-
По каким признакам классифицируются погрешности измерения?
Погрешности измерения так же могут быть классифицированы по ряду признаков, в частности:
а) по способу числового выражения;
б) по характеру проявления;
в) по виду источника возникновения (причин возникновения).
-
Назовите и охарактеризуйте основные виды погрешностей измерений.
Абсолютная погрешность измерения (∆x) представляет собой разность между измеренной величиной и действительным значением этой величины.
Относительная погрешность измерения (δ) представляет собой отношение абсолютной погрешности измерения к действительному значению измеряемой величины.
Систематическая погрешность измерения (∆с) – это составляющая погрешности результата измерений, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же физической величины.
Случайная погрешность измерения (∆0) – составляющая погрешности результата измерений, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях, проведенных с одинаковой тщательностью, одной и той же физической величины.
Грубые погрешности (промахи) возникают из-за ошибочных действий оператора, неисправности СИ или резких изменений условий измерений (например, внезапное падение напряжения в сети электропитания).
Погрешности метода – это погрешности, обусловленные несовершенством метода измерений, приемами использования средств измерения, некорректностью расчетных формул и округления результатов, проистекающие от ошибочности или недостаточной разработки принятой теории метода измерений в целом или от допущенных упрощений при проведении измерений.
Инструментальные составляющие погрешности – это погрешности, зависящие от погрешностей применяемых средств измерений.
Субъективные составляющие погрешности – это погрешности, обусловленные индивидуальными особенностями наблюдателя.
-
Как определить погрешность записи числа?
Погрешность записи (округления) числа определяется как отношение половины единицы младшего разряда числа к значению числа.
-
Как определить погрешность результата косвенного измерения?
При косвенных измерениях искомое значение величины находят расчетом на основе прямых измерений других физических величин, функционально связанных с искомой величиной известной зависимостью
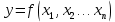
где x1 ,x2 ,...,xn – подлежащие прямым измерениям аргументы функции y.
Результатом косвенного измерения является оценка величины у, которую находят подстановкой в формулу измеренных значений аргументов хi.
Способ 1. Этот способ рекомендуется для таких уравнений измерения, которые содержат суммы и разности аргументов. Сначала находится абсолютная, а затем относительная погрешности. Общая формула для расчета абсолютной погрешности при косвенных измерениях физической величины y для произвольного вида f функции имеет вид:
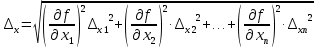
Для нахождения относительной погрешности нужно прежде всего найти среднее значение величины y. После этого определить относительную погрешность.
Способ 2. Этот способ определения погрешности косвенных измерений отличается от первого способа меньшими математическими трудностями, поэтому его чаще используют. В начале находят относительную погрешность, и только затем абсолютную. Особенно удобен этот способ, если уравнение измерения содержит только произведения и отношения аргументов.