Файл: Федеральное агентство по рыболовству Федеральное государственное бюджетное образовательное.docx
Добавлен: 29.10.2023
Просмотров: 18
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное агентство по рыболовству
Федеральное государственное бюджетное образовательное
учреждение высшего образования
«Астраханский государственный технический университет»
Система менеджмента качества в области образования, воспитания, науки и инноваций сертифицирована DQS
по международному стандарту ISO 9001:2015
Институт нефти и газа
Кафедра «Технологические машины и оборудование»
Направление: 18.04.02 «Энерго- и ресурсосберегающие
процессы в химической технологии, нефтехимии и биотехнологии»
Направленность «Машины и аппараты химических производств»
Реферат по дисциплине:
«Энергосбережение в химико-технологических системах»
Работа выполнена
ст. гр. ДНРММ-11 Бисалиева Э.Р
Проверил: доц Титова Л.М
Астрахань 2022
Равновесными процессами называются такие, которые протекают бесконечно медленно через совокупность равновесных состояний системы. Поэтому в каждый момент можно утверждать, что система находится в состоянии равновесия (хотя протекает процесс). Можно также сказать, что в случае равновесного процесса силы действия на систему уравновешиваются силами противодействия со стороны системы. Причем, если изменить знак силы на противоположный, то начнется обратный процесс. Получается, что равновесный процесс относится к двусторонним процессам.
Также считается, что в случае равновесного процесса совершаемая системой работа максимальна. Для иллюстрации этого высказывания обычно приводится пример с идеальным газом, находящимся в сосуде под поршнем, на котором расположены гирьки. Если постепенно уменьшать вес этих гирек, каждый раз снимая с поршня некоторое конечное количество гирек, то линия перехода системы из одного состояния в другое (рис. 1) будет иметь вид ломанной линии (сплошная линия). Работа, совершаемая системой при таком изменении давления будет равна площади рисунка под этой ломанной линией. Если же уменьшать давление на поршень за счет бесконечно малых количеств уменьшения давления dp, то на рис.1 линия перехода системы из начального состояния в конечное
будет иметь вид штриховой линии и работа, совершаемая системой в этом случае будет максимальной.
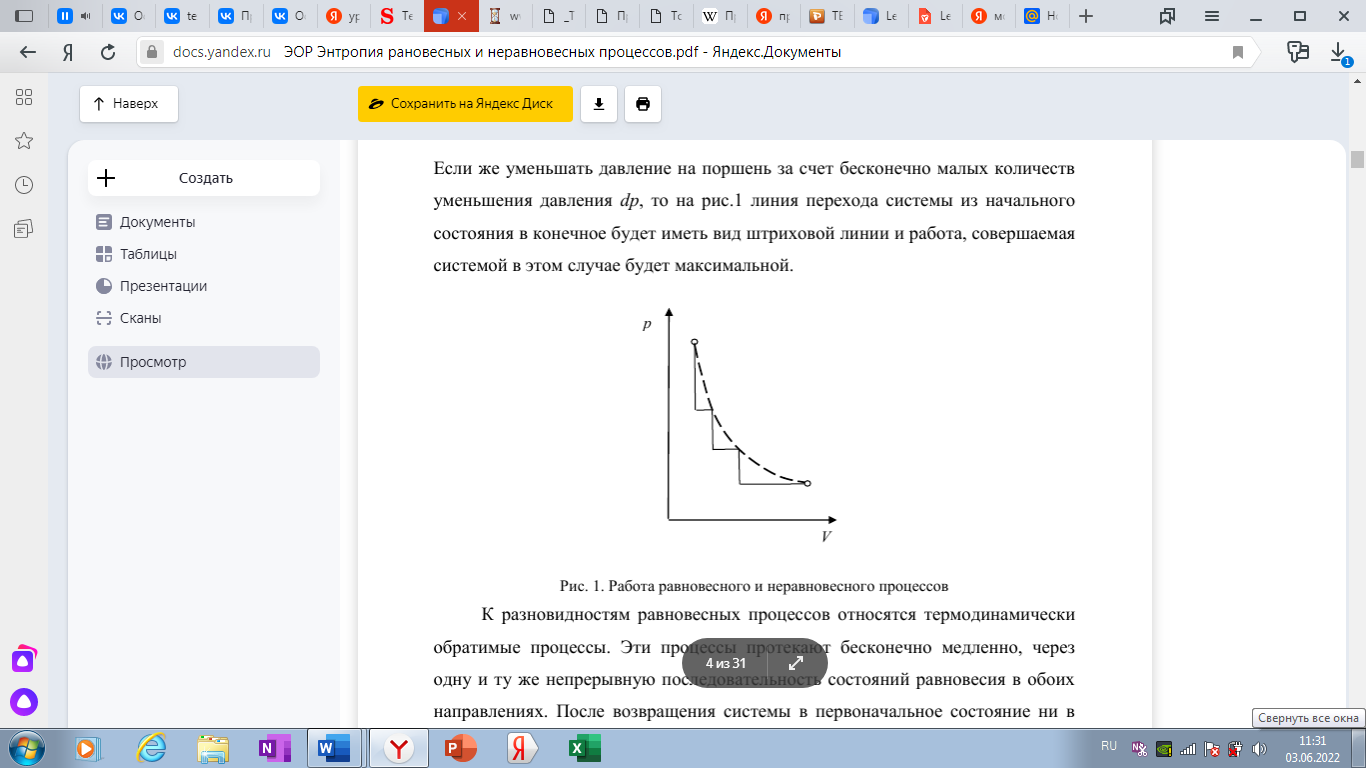
Рис. 1 Работа равновесного и неравновесного процессов
К разновидностям равновесных процессов относятся термодинамически обратимые процессы. Эти процессы протекают бесконечно медленно, через одну и ту же непрерывную последовательность состояний равновесия в обоих направлениях. После возвращения системы в первоначальное состояние ни в окружающей среде, ни в самой системе не остается никаких изменений.
В большинстве случаев понятие равновесного процесса и обратимого процесса совпадают.
Неравновесные процессы – это реально наблюдаемые на опыте процессы, который протекают не с бесконечно малой, а с конечной скоростью. Это обусловлено конечной разностью в действующих силах на систему: существенной разностью в давлениях и температурах между системой и внешней средой, например. В этом случае, если мы прекратим внешнее воздействие, то процесс сам по себе не прекратится. Например, если воздействие было в виде температуры, то нагревание, само собой распространяется вглубь системы до тех пор, пока не наступит состояние равновесия, например, пока температура в разных частях системы не станет одинаковой. Отсюда можно сделать вывод о том, что неравновесный процесс является односторонним.
Работа, совершаемая системой в этом процессе, меньше, чем в равновесном, так как часть энергии тратится на преодоление различного рода сопротивлений и превращается в бесполезную теплоту.
Неравновесные процессы это процессы, включающие неравновесные состояния. Примеры неравновесных процессов:
процесс установления равновесия в системе, находившейся ранее в неравновесном состоянии;
химическая реакция;
диффузия;
теплопроводность;
перенос электрического тока в растворах электролитов;
переход системы из одного неравновесного состояния в другое под влиянием внешних возмущений.
Неравновесные процессы являются необратимыми процессами, связанными с производством энтропии.
Классическая термодинамика изучает термодинамические (обратимые) процессы. Для неравновесных процессов она устанавливает лишь неравенства, которые указывают возможное направление этих процессов. Неравновесным процессам посвящена особая термодинамика – термодинамика неравновесных процессов. Главная задача этой термодинамики заключается в количественном изучении неравновесных процессов, в частности в определении их скоростей в зависимости от внешних условий. Системы, в которых протекают неравновесные процессы, рассматриваются как непрерывные среды, а их параметры состояния как полевые переменные, то есть непрерывные функции координат и времени.
Для макроскопического описания неравновесных процессов применяют следующий метод: систему представляют состоящей из элементарных объёмов, которые всё же настолько велики, что содержат очень большое число молекул.
Расчет изменения энтропии в неравновесных процессах
Главным приемом при расчете энтропии в случае неравновесных процессов является замена одного неравновесного пути изменения на серию из равновесных отрезков этого пути с условием, что начальное и конечное состояния и в том и в другом случае будут совпадать. Например, пусть вещество А из твердого состояния при температуре T1 нужно перевести в жидкое состояние при температуре T2 . При определенной температуре в интервале температур T1 T2 вещество должно расплавиться, то есть будет фазовое превращение. По справочнику определяем эту температуру, Tпл. Заменяем такой неравновесный процесс на серию из трех равновесных процессов:
нагрев твердого вещества А от температуры T1 до температуры плавления Tпл;
плавление вещества А при температуре плавления Tпл;
нагрев жидкого вещества А от температуры плавления Tпл до температуры T2.
Следовательно полное изменение энтропии будет равно будет равно сумме трех слагаемых:
S S1 S2 S3.
Первое слагаемое справа – это изменение энтропии при нагреве твердого вещества от температуры T1 до температуры плавления. Эта величина находится как
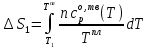
Второе слагаемое – это изменение энтропии при фазовом превращении:
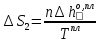
Третье слагаемое – это изменение энтропии при дальнейшем нагреве уже образовавшейся жидкости от температуры плавления до температуры T2
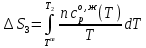
Абсолютная мольная энтропия вещества при температуре Т может быть найдена. Например, нас интересует значение мольной энтропии некоторого газообразного вещества. Мы найдем ее как сумму изменений мольной энтропии в следующих процессах: нагрев исследуемого вещества в твердом состоянии от нуля до температуры плавления; процесс плавления; нагрев жидкого вещества до температуры кипения; испарение жидкости; нагрев полученного газообразного вещества до нужной температуры.
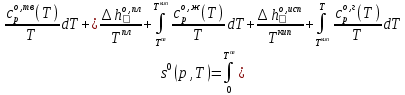
В справочных термодинамических таблицах обычно приводят значения абсолютной энтропии в стандартном состоянии при температуре 298 К sоk,298 . Тогда расчет абсолютного значения энтропии при какой-либо другой температуре можно произвести исходя из значения энтропии при 298 К, учитывая агрегатное состояние исследуемого вещества при 298 К по формуле
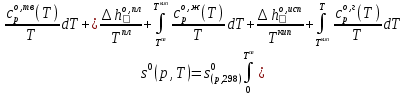
Изменение энтропии при химической реакции
Рассмотрим, как можно выразить из фундаментального уравнения Гиббса изменения энтропии deS и diS . Запишем фундаментальное уравнение Гиббса и балансовое соотношение для числа молей компонента k:
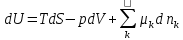
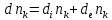
В балансовом соотношении
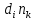– изменение числа молей за счет химического превращения; 
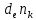– изменение количества вещества за счет обмена веществом с окружающей средой.Гиббс, выводя уравнение (3), не рассматривал химическое превращение, но рассматривал обратимый обмен теплотой и веществом. А обратимый обмен
энергией и веществом характеризует изменение энтропии deS, поэтому
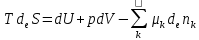
или в явном виде выражая deS:
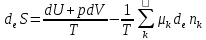
Теофил Де Донде доказал, что изменение энтропии, возникающее в закрытой системе с протекающим в ней химическим превращением, равно «некомпенсированной теплоте» Клаузиуса, т. е.
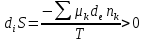
Изменение числа молей вещества k при протекании химической реакции в закрытой системе связано с глубиной химической реакции
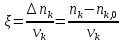
Отсюда справедливо соотношение
dnk kd dink.
Очень важная характеристика химического превращения – химическое сродство реакции r равно
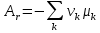.Учитывая выражения числа молей вещества за счет химического превращения и выражение химического сродства реакции r, получим
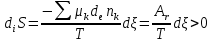
Установим связь между химическим сродством реакции и скоростью реакции. Скорость возникновения энтропии определяется по уравнению
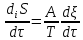
Рассмотрим обратимую реакцию A + B ⇄ C.
Скорость прямой стадии будет равна wпр kпрcAcB, а скорость обратной
стадии wобр kобрcС.
Общая скорость реакции может быть найдена по уравнению
w kпрcAcB kобрcС.
(5)
С другой стороны скорость химической реакции в системах постоянного объема равна
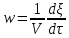
Объединяя приведенные соотношения (5) и (6), получаем дифференциальное уравнение скорости реакции:
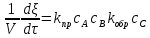
Запишем подробнее, чему равно химическое сродство рассматриваемой реакции:
где k – стехиометрическое число компонента k, а k – его химический потенциал.
Ar A B C.
Преобразуем это выражение
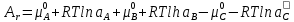
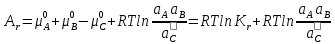
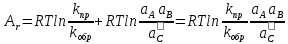
Из этого уравнения видна связь между химическим сродством и скоростью реакции
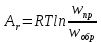
Скорость реакции связана и со скоростью возникновения энтропии в единице объема. При подстановке соотношения, выражающего химическое сродство реакции через скорости стадий (7) в уравнение (4) получим:
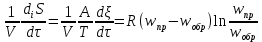
В полученном уравнении (7) по второму закону термодинамики правая часть всегда неотрицательна. Это уравнение можно обобщить для системы, в которой одновременно протекает несколько реакций. В этом случае скорость возникновения энтропии в единице объема будет равна сумме энтропий, произведенных каждой реакцией:
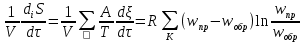
Решение полученного дифференциального уравнения позволит в явном виде выразить скорость возникновения энтропии в неравновесном процессе - химической реакции в зависимости от времени. Рассмотрим зависимостиn некоторых термодинамических функций, характеризующих обратимую мономолекулярную реакцию рацемизации между двумя зеркально симметричными молекулами – энантиомерами некоторой хиральной молекулы от времени и от глубины химической реакции. Рацемизация описывается кинетикой первого порядка, причем константы скорости прямой и обратной реакций k одинаковы из-за симметрии: энантиомер L превращается в энантиомер D с такой же константой скорости, как D превращается в L согласно уравнению L⇄D.