1. 
   Понятие марковского процесса, его роль в построении ТМО.
   

Для системы массового обслуживания характерен случайный процесс. Изучение случайного процесса, протекающего в системе, выражение его математически и является предметом теории массового обслуживания.Математический анализ работы системы массового обслуживания значительно облегчается, если случайный процесс этой работы является марковским. Процесс, протекающий в системе, называется марковским, если в любой момент времени вероятность любого состояния системы в будущем зависит только от состояния системы в текущий момент и не зависит от того, каким образом система пришла в это состояние. При исследовании экономических систем наибольшее применение имеют марковские случайные процессы с дискретными и непрерывными состояниями.Случайный процесс называется процессом с дискретными состояниями, если все его возможные состояния можно заранее перечислить, а сам процесс состоит в том, что время от времени система скачком переходит из одного состояния в другое.Случайный процесс называется процессом с непрерывным состоянием, если для него характерен плавный, постепенный переход из состояния в состояние.Также можно выделить марковские процессы с дискретным и непрерывным временем. В первом случае переходы системы из одного состояния в другое возможны только в строго определенные, заранее фиксированные моменты времени. Во втором случае переход системы из состояния в состояние возможен в любой, заранее неизвестный, случайный момент. Если вероятность перехода не зависит от времени, то марковский процесс называют однородным.В исследовании систем массового обслуживания большое значение имеют случайные марковские процессы с дискретными состояниями и непрерывным временем.Исследование марковских процессов сводится к изучению матриц переходных вероятностей (

---

). Каждый элемент такой матрицы (поток событий) представляет собой вероятность перехода из заданного состояния (которому соответствует строка) к следующему состоянию (которому соответствует столбец). В этой матрице предусмотрены все возможные переходы данного множества состояний. Следовательно, процессы, которые можно описывать и моделировать с помощью матриц переходных вероятностей, должны обладать зависимостью вероятности конкретного состояния от непосредственно предшествующего состояния. Так выстраивается цепь Маркова. При этом цепью Маркова первого порядка называется процесс, для которого каждое конкретное состояние зависит только от его предшествующего состояния. Цепью Маркова второго и более высоких порядков называется процесс, в котором текущее состояние зависит от двух и более предшествующих.

2. 
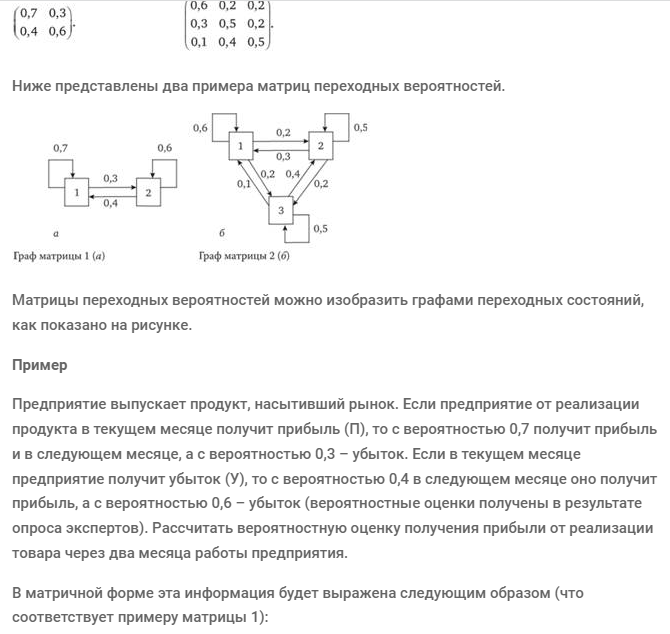
   Классификация моделей СМО по признакам применительно к задачам анализа дискретных процессов и систем.
   

При моделировании реальных систем с дискретными процессами достаточно широкое применение находят базовые модели в виде СМО, которые могут быть классифицированы (рис. 2.5):

• 
  • по числу мест в накопителе;
  
• 
  • числу обслуживающих приборов;
  
• 
  • количеству классов заявок, поступающих в СМО;
  
• 
  • надежности.
  

• 
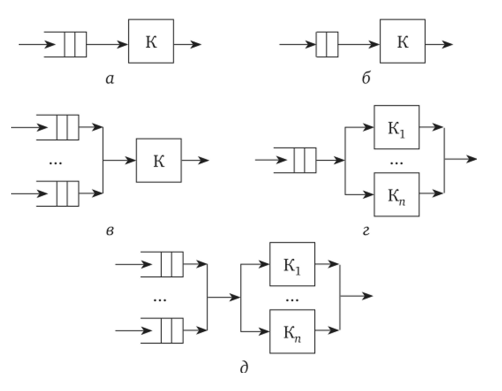
  1. По числу мест в накопителе СМО делятся на системы:
  
  • 
    • без накопителя (СМО с отказами), в которых заявка, поступившая на вход системы и заставшая все приборы занятыми обслуживанием заявок более высоких приоритетов, получает отказ и теряется;
    
  • 
    • с накопителем ограниченной емкости (СМО с потерями)
    
  • 
    (рис. 2.5, б), в которых поступившая на вход системы заявка теряется, если она застает накопитель заполненным полностью;
    
  • 
    • системы с накопителем неограниченной емкости (СМО без потерь) (рис. 2.5, а, в, г, д), в которых любая поступившая заявка всегда помещается в накопитель для ожидания обслуживания.
    

---

Как отмечалось ранее, предположение о неограниченной емкости накопителя может использоваться для моделирования реальных систем, в которых вероятность потери заявки из-за переполнения накопителя ограниченной емкости меньше Ю^-3.

• 
  2. По количеству обслуживающих приборов СМО делятся:
  
  • 
    • на одноканальные (см. рис. 2.5, а, б, в), содержащие один канал К;
    
  • 
    • многоканальные (см. рис. 2.5, г, д), содержащие п обслуживающих приборов К₂, ..., К„, п > 1.
    

В многоканальных СМО обычно предполагается, что все каналы идентичны и равнодоступны для любой заявки, т.е. при нескольких свободных каналах поступившая заявка с равной вероятностью может попасть в любой из них на обслуживание. При ИМ некоторых реальных систем неразличимость каналов вызывает определенные трудности, например при ИМ автоматической телефонной станции, которая обслуживает большое количество абонентов. Каждый из этих абонентов должен быть идентифицирован (иметь номер). При условии идентичности идентификация в многоканальных СМО отсутствует.

• 
  По количеству классов (типов) заявок, поступающих в СМО, различают системы:
  
  • 
    • с однородным потоком заявок (см. рис. 2.5, а, б, г);
    
  • 
    • неоднородным потоком заявок (см. рис. 2.5, в, д).
    

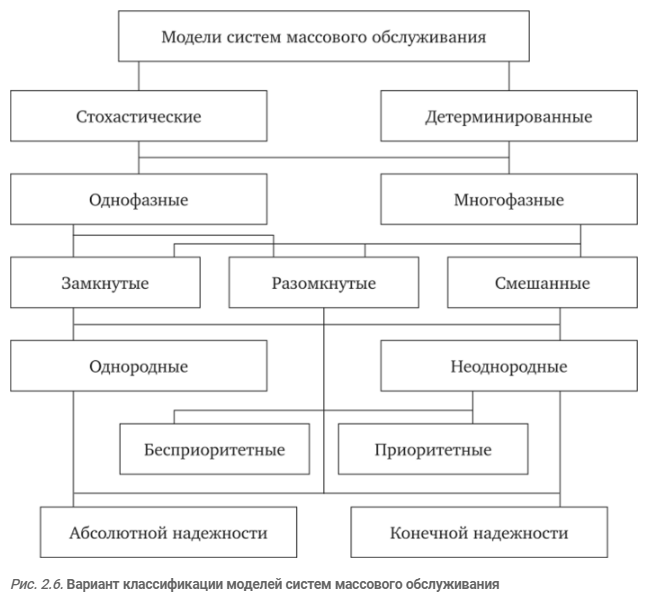
Однородный поток заявок образуют заявки одного класса, а неоднородный поток — это поток заявок нескольких классов.Ранее мы отметили, по каким признакам производится разделение множества поступающих в СМО заявок на классы: по длительности обслуживания и приоритетам. Если эти признаки идентичны, то заявки относятся к одному классу.В зависимости от структуры и свойств исследуемых систем их моделями могут служить СМО различных классов. Одна из возможных классификаций моделей приведена на рис. 2.6.

• 
  4. В зависимости от характера процессов поступления и обслуживания заявок СМО делятся:
  
  • 
    • на стохастические, в которых хотя бы один из интервалов поступления или длительности обслуживания заявок одного класса или разных классов или все они носят случайный характер;
    
  • 
    • детерминированные, в которых интервалы всех поступающих заявок и длительности их обслуживания являются детерминированными величинами.
    

3. 
   Сравнение методов математического и имитационного моделирования по области применения, по критериям сложности построения модели и точности вычисления характеристик моделируемой системы, по адекватности модели реальному объекту или процессу.
   

---

Метод математического моделирования, представляющий собой количественное описание изучаемых явлений на языке математики, широко применяется для исследования всевозможных явлений природы и общественной жизни. Этот «третий путь познания» сочетает в себе достоинства как теории, так и эксперимента.К имитационному моделированию прибегают, когда: дорого или невозможно экспериментировать на реальном объекте; невозможно построить аналитическую модель: в системе есть время, причинные связи, последствие, нелинейности, стохастические (случайные) переменные; необходимо сымитировать поведение системы во времени.Математическое моделирование является универсальным инструментом для исследования сложных технических систем, к которым относится здание как единая энергетическая система.Для имитационного моделирования характерно вос- произведение явлений, описываемых моделью, с сохранением их логической структу- ры, последовательности чередования во времени, взаимосвязей между параметрами и переменными исследуемой системы.С помощью имитационного моделирования нельзя изучать:

• 
  процессы психологического взаимодействия людей
  
• 
  траектории движения планет и космических кораблей
  
• 
  инфляционные процессы в промышленно-экономических системах
  
• 
  тепловые процессы, протекающие в технических системах.
  

Каким способом можно построить АКФ Численно, автокорреляционная функция представляет собой последовательность коэффициентов корреляции между исходным рядом, и его копией, сдвинутой на заданное число интервалов ряда

---

Смотрите также файлы

• Автоматизированное рабочее место преподавателя.docx

• М. Р. Битянова считает, что сопровождение это система профессиональной деятельности педагогического сообщества, направленная на создание социальнопсихологических условий для успешного обучения и психологического.docx

• Оформление и составление документов о разработке концепции и вопросов для гуфсин.docx

• Задание на км2 Сформировать таблицу значений случайного процесса. Для этого выбрать участок дороги или магазин и зафиксировать по наблюдениям количество событий и их моменты возникновений в интервалах по 20 минут за сутки..docx

• Обучающийся Мазунина Ксения Сергеевна Преподаватель Старкова Татьяна Андреевна Практическое занятие.docx