Российский государственный социальный университет

ИТОГОВОЕ ПРАКТИЧЕСКОЕ ЗАДАНИЕ

по дисциплине «Теория вероятности»

ФИО студента	Сафронова Александра Александровна
Направление подготовки	Бизнес - информатика
Группа	БИЗ-Б-01-З-2020-1_ДИСТАНТ

Москва 2023

1. 
   У Пети есть 7 книг, а у Егора – 9 книг. Сколькими способами они могут обменять три книги одного на три книги другого?
   
   
   

Ответ: 2940

2. 
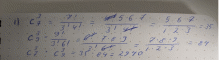
   Из колоды в 52 листа вынимается одна карта наугад. Какова вероятность того, что это будет туз или дама?
   
   
   

Ответ: 8/52

3. 
   В вазе находится 10 конфет «Белочка», 6 конфет «Вдохновение», 4 конфеты «Шальная пчелка». Ребенок наугад берет 6 конфет. Какова вероятность, что среди них будет 4 конфеты «Белочка» и 2 конфеты
   

«Шальная пчелка»?

Ответ: 0,0325

4. 
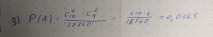
   Какова вероятность того, что три случайно встреченных на улице человека родились в понедельник?
   

Ответ: 1/343

5. 
   Фирма получает товар через трех посредников. Вероятности того, что посредник будет выполнять условия договора поставки в течение времени T, соответственно равны 0,8; 0,9; 0,9. Посредники могут
   

нарушить договор независимо друг от друга. По истечении времени

---

T выяснилось, что товар на фирму не поступил. Найти вероятность того, что договор нарушил только третий посредник.

Ответ: Искомая вероятность будет равна произведению трёх вероятностей: вероятности того, что первый посредник НЕ нарушил договор, вероятности того, что второй посредник НЕ нарушил договор и вероятности того, что третий посредник нарушил договор: P = 0,8*0,9*(1 - 0,9) = 0,072.

6. 
   Вероятность продажи акций с прибылью через год после покупки равна 0,8. независимо было продано 5 акций. Найти вероятность того, что прибыль будет получена ровно с двух из них.
   
   Ответ: 0,0512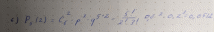
   
   

7. 
   Баскетболист бросает мяч в корзину. Вероятность попадания мяча при каждом броске равна 0,7. Найдите вероятность того, что из 100 бросков баскетболист попадет ровно 75 раз.
   Ответ: 0,0484
   
   
   
8. 
   Дискретная случайная величина ???? задана рядом распределения:
   

????	-14	-13	-11	11	13
????	0,2	????	0,25	0,15	0,25

Найти:

а) неизвестную вероятность ????;

б) функцию распределения????(????) и построить её график;

в) математическое ожидание????[????];

г) дисперсию????[????];

д) ???? ⁽−14 <???? ≤ 11) .

Ответ:
а) 0, 15
б)



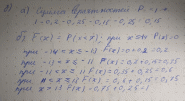
в) -2, 6
г) -41,16
д) 0,6

9. 
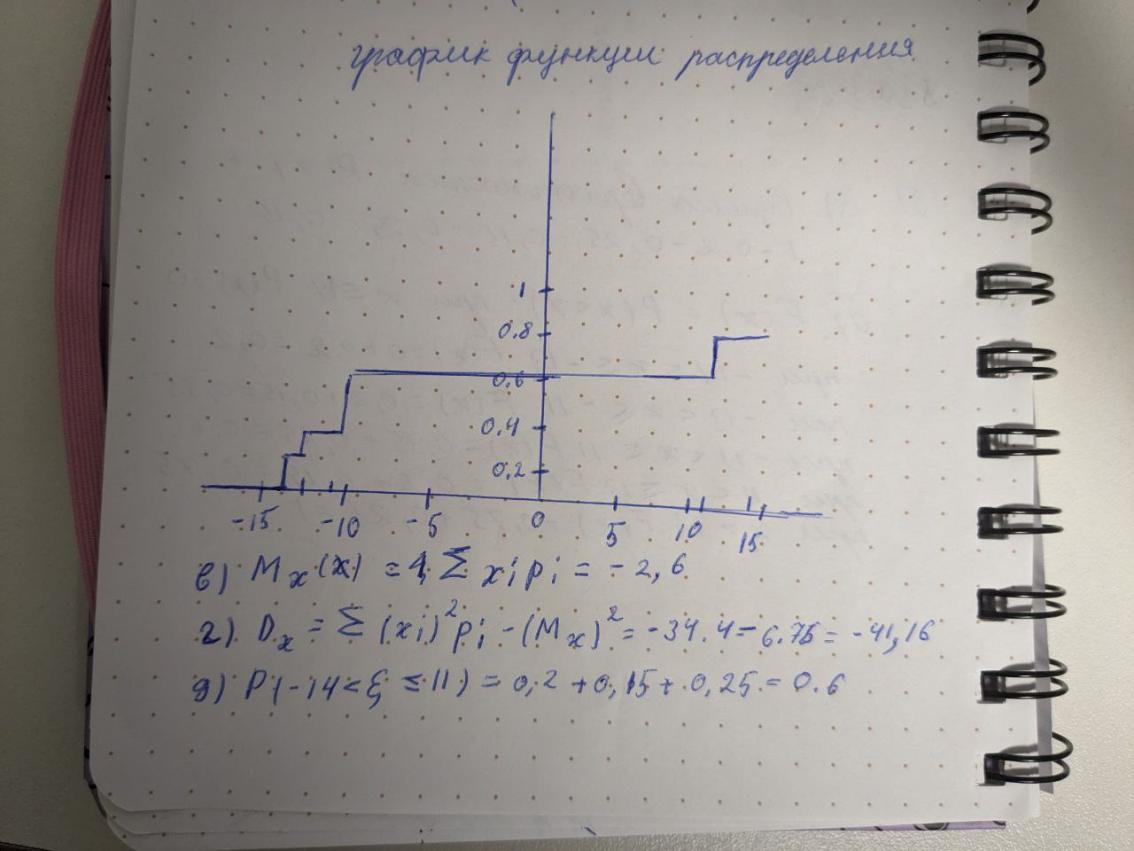
   Студент знает 6 из 10 вопросов зачета. В билете три вопроса. Случайная величина ???? – количество вопросов из билета, которые студент знает. Построить вероятностный ряд для????. Найти ее ????[????] и
   

????[????].

a) 1,801
б) 3

---

10. 
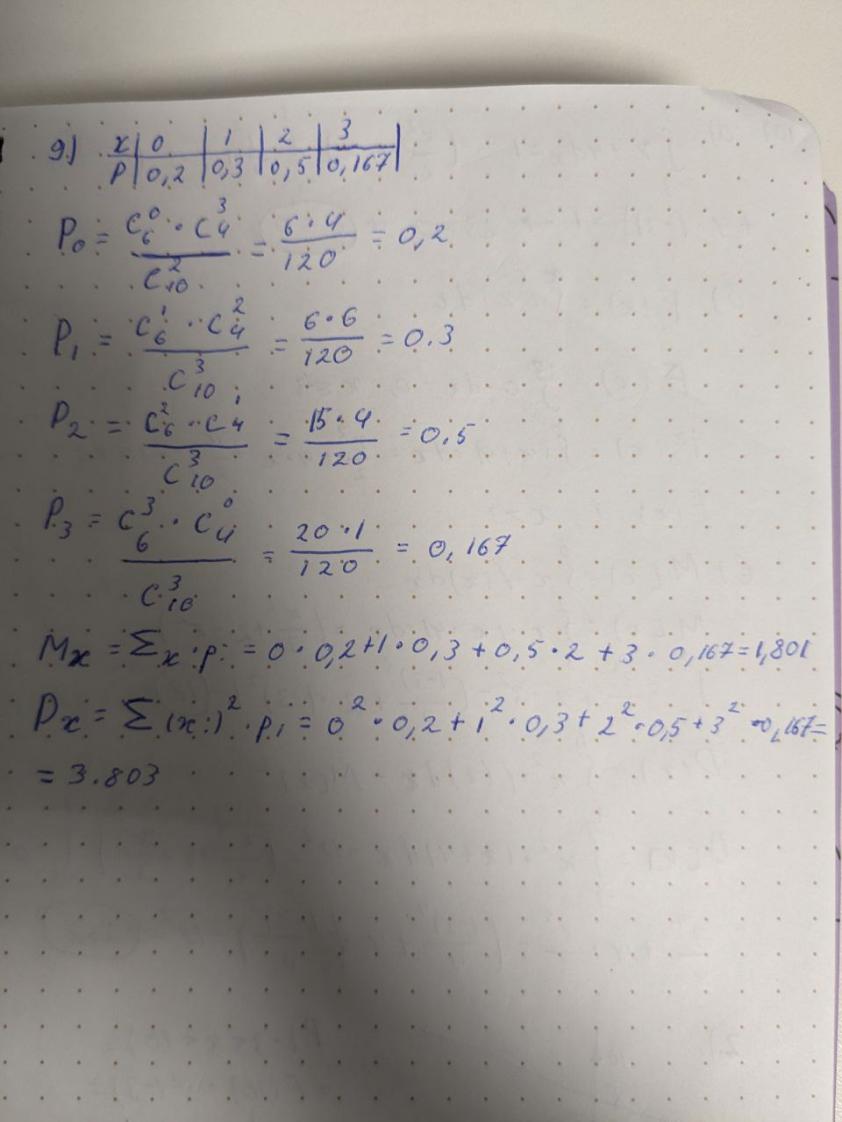
    Непрерывная случайная величина ???? задана с помощью функции плотности распределения вероятностей????(????):
    

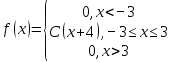
Найти: а) параметр ????;

б) функцию распределения????(????) и построить ее график;

в) математическое ожидание????[????]и дисперсию ????[????];

г) ???? ⁽−3 <???? ≤ 10).

а) С = 0

11. 
    Ответ:
    
    
    

12. 
    Случайная величина ???? распределена нормально с математическим ожиданием ????[????] = 1 и дисперсией ???? ???? = 9. Написать ее функцию плотности распределения вероятностей???? ???? и вычислить ????(−5 ≤ ???? ≤ 7).
    

Ответ: 1, 56

---

Смотрите также файлы

• Введение стр Волонтерство стр.doc

• Характеристики заданий и система оценивания 5 класс.docx

• Реферат человек и природа роман м. А шолохова тихий дон Выполнила ст гр гд114 Печникова И. Д.docx

• Методические указания по изучению дисциплины для студентов заочной формы обучения и миппс специальности 13. 03. 02 Электроэнергетика и электротехника.doc

• Методические указания по выполнению контрольной работы прошли экспертизу методического отдела Утверждено на заседании кафедры инноваций и предпринимательства.pdf