Файл: Кафедра конструкторско технологическое обеспечение машиностроительных производств 15. 03.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 20
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образования
«Тольяттинский государственный университет»
Институт Машиностроения
(наименование института полностью)
Кафедра конструкторско - технологическое обеспечение машиностроительных производств (15.03.05)
(код и наименование направления подготовки, специальности)
Технология машиностроения
(направленность (профиль) / специализация)
Практическое задание № 5
по учебному курсу «Высшая математика 2»
Вариант 3
| Обучающегося | Наталья Сергеевна Зуевич | |
| | (И.О. Фамилия) | |
| Группа | ТМбп-2001бс | |
| | | |
| Преподаватель |
| |
| | (И.О. Фамилия) | |
Тольятти 2023
Бланк выполнения задания 5
| № п/п | Задача | Ответ |
| 1. | Вычислить объём тела, заданного представленными уравнениями, используя его поперечные сечения: | |
| Условие задачи: |  | |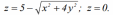
| Чертёж: |  | |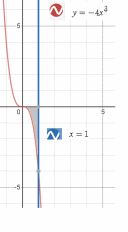
| Подробное решение: | VOx=π∫10(−4x3)2dx=π∫10(16x6)dx=16π⋅x77|10=167π Возводим в квадрат: (z−4)2=y2+2z2 z2+8z+y2−16=0 z2+8z+16+y2−32=0 (z+4)2+y2=32 – это уравнение эллипса в пл уOz, а значит цилиндрической поверхности в пространстве Это бесконечная поверхность, вдоль оси Ох. См. рис. По условию ограничена пл. х=5 Получается с одной стороны. А значит тело неограниченное. x=4+  x−4= Возводим в квадрат и получаем: (x−4)2=y2+2z2 – это коническая поверхность. Эллиптический конус в с вершиной в точке (4;0;0) Рассекаем этой слой плоскостью x=h 4 < h < 5, в сечении получим эллипс Площадь эллипса x2a2+y2b2=1 равна πab Площадь эллипса зависит от h и равна S(h)=π⋅(h−4)⋅(h−4)2√ V=∫54S(x)dx Где вместо S(x) это S(h) при h=x V=∫54S(x)dx=∫54π⋅(x−4)⋅(x−4)2√dx=π2√∫54(x−4)2dx==π2√⋅((x−4)33|54=π32√ | |
| 2. | Вычислить объём тела, образованного вращением вокруг оси Ox фигуры, заданной представленными линиями: | |
| Условие задачи: |  | |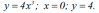
| Чертёж: |  | |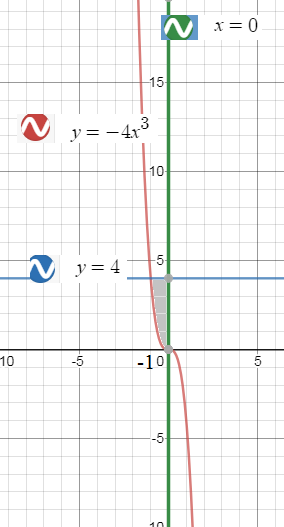
| Подробное решение: | Vтела вращения=Vцилиндра–V(криволинейного конуса)= =π ∫ 0–1(42– (–4x3)2)dx=πR2·H– 16π ∫ 0–1(x6)2dx= =π·42·1–π(16x7/7)|0–1= =16π–π·(16/7)=96π/7 | |